各种数学知识1

Update on 2019.3.21

 

筛法

 

线性筛那一套.jpg

 1 //欧拉函数
 2 int npr[N],pri[N],phi[N];
 3 void Getphi()
 4 {
 5     npr[1]=true,phi[1]=1;
 6     for(int i=2,cnt=0;i<=Maxx;i++)
 7     {
 8         if(!npr[i]) pri[++cnt]=i,phi[i]=i-1;
 9         for(int j=1,p;j<=cnt&&(p=i*pri[j])<=Maxx;j++)
10         {
11             npr[p]=true,phi[p]=phi[i]*pri[j];
12             if(i%pri[j]==0) break;
13             else phi[p]-=phi[i];
14         }
15     }
16 }

 1 //莫比乌斯函数
 2 int npr[N],pri[N],mul[N];
 3 void Getmul()
 4  {
 5      npr[1]=true,mul[1]=1;
 6      for(int i=2,cnt=0;i<=Maxx;i++)
 7      {
 8          if(!npr[i]) pri[++cnt]=i,mul[i]=-1;
 9          for(int j=1;j<=cnt&&i*pri[j]<=Maxx;j++)
10           {
11              npr[i*pri[j]]=true;
12              if(i%pri[j]==0) break;
13              else mul[i*pri[j]]=-mul[i];
14          }
15      }
16 }

 1 //因子数
 2 int npr[N],pri[N],fac[N],mpw[N];
 3 void Getfac()
 4 {
 5     npr[1]=true,fac[1]=1;
 6     for(int i=2,cnt=0;i<=Maxx;i++)
 7     {
 8         if(!npr[i]) 
 9             pri[++cnt]=i,fac[i]=2,mpw[i]=1;
10         for(int j=1,p;j<=cnt&&(p=i*pri[j])<=Maxx;j++)
11         {
12             npr[p]=true;
13             if(i%pri[j]==0) 
14             {
15                 fac[p]=fac[i]/(mpw[i]+1)*(mpw[i]+2);
16                 mpw[p]=mpw[i]+1; break;
17             }
18             else
19                 fac[p]=2*fac[i],mpw[p]=1; 
20         }
21     }
22 }

埃筛筛区间(比如什么1e12->1e12+1e7这种)

要求：先普通地筛到根号级别

 1 //假设已经筛出来了根号级别的
 2 #define lli long long
 3 const int N=1e6+60;
 4 int cnt,pri[N],npr[N],npm[N];
 5 void ex_Eratosthenes(lli l,lli r)
 6 {
 7     for(int i=2;1ll*i*i<=r;i++)
 8         if(!npr[i])
 9             for(lli j=l/i*i;j<=r;j+=i) 
10                 if(j>=l) npm[j-l]=true;
11 }

杜教筛

我的链接

洲阁筛&Min25筛

咕咕咕

---

 

一些关于因数的东西

 

1.若将正整数n以算术基本定理表示为$2^a* 3^b* ...p(n)^x$，则这个数的因子个数为$(a+1)*(b+1)* ...* (x+1)$，其因子和$Sum=\prod\limits_{i=1}^{n}\sum\limits_{j=0}^{k_i}{p_i}^j$

2.1e?以内因子数最多的数及其因子个数

 

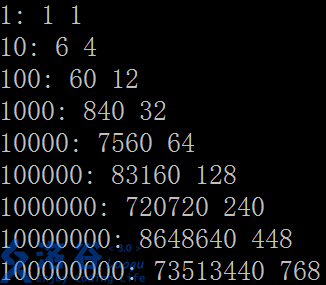
另外的：

int以内2095133040有最多的因子数，它总共有1600个因子

long long以内9200527969062830400有最多的因子数，它总共有161280个因子

---

东拼西凑的一些东西

 

斐波那契序列各项的公约数 

$gcd(fib[n],fib[m])=fib[gcd(n,m)]$

斐波那契数列前缀和

$fsum[i]=fib[i+2]-1$

欧拉定理及其扩展

$a^n≡a^{n\mod φ(p)}$ $mod$ $p$

扩展(p不一定为质数)：$a^n≡a^{n \mod φ(p)+φ(p)}$ $mod$ $p$ $(n>=φ(p))$

 

更相减损(辗转相除的基础)

$gcd(a,b)=gcd(a,a-b)$

裴蜀定理

若$a,b$是整数,且$gcd(a,b)=d$，那么对于任意的整数$x,y$,$ax+by$都一定是$d$的倍数。同时一定存在整数$x',y'$,使$ax+by=d$成立。

裴蜀定理的扩展

设$a_1,a_2......a_n$为n个整数，$d$是它们的最大公约数，那么一定存在整数$x_1,x_2,x_3......x_n$，使得$x_1*a_1+x_2*a_2+...x_n*a_n=d$。
特别地，如果$a_1,a_2,a_3...a_n$互质，那么一定存在整数$x_1,x_2......x_n$使得$x_1*a1_+x_2*a_2+...x_n*a_n=1$。

 

威尔逊定理

$(p-2)! \equiv 1(mod$ $p)$(p为质数)

 

不知是啥

一个b进制最简分数是有限循环小数当且仅当其分母没有与b不同的质因子