模板汇总2.5_图论5
1.轻重链剖分
先放个祖传轻重链剖大佬communist的讲解(感谢提供图片)
①轻重链剖分是什么
一种树上统计的方法,可以处理链的修改和查询。
准备对这棵树进行轻重链剖分↓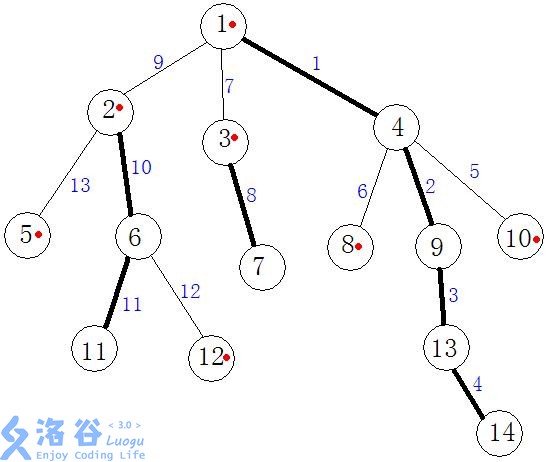
②轻重链剖分的原理
首先明确两个定义:重儿子和轻儿子。重儿子指一个节点所有儿子中所有子树最大的儿子,剩下的节点自然是轻儿子了(上图中标有红点的是轻儿子,没标的是重儿子)
有了这个定义我们可以再引出重边和轻边的定义:连有重儿子的边叫重边,其余的边叫轻边。进一步的,我们定义重边连成的路径叫重链。特别的,我们认为叶节点自己是一条重链。
然后我们先DFS一通搞出一些基本的信息,同时求出每个点的重儿子
然后引入一个$top$数组,表示每个点所在重链的“顶端”(深度最小的节点),再DFS一遍求出每个点的$top$,具体实现是先走重儿子(参见上面的讲解和重儿子的定义),然后如果还有儿子就说明这个儿子就是它下面一条重链的$top$,再走一下
现在考虑如何维护/查询了
做法是让两点中深度较大的直接跳到当前重链的$top$,同时修改跳的这一段,再沿着当前$top$上面的这一条轻边走到下一条重链上,最终两个点处在一条重链上时直接修改,同理可以求LCA
那么复杂度为什么对呢?因为从一个点出发向根节点跳经过的重链和轻边都不超过$\log n$
证明:因为轻儿子对应的子树大小小于父节点对应的子树大小的一半,所以沿着一条轻边跳到下一条重链时,所在节点的子树大小至少翻倍,那么轻边就是$\log n$级别的;又因为重链是被轻边连起来的,所以重链也是$\log n$级别的。
③轻重链剖分的时间复杂度与所需空间
时间复杂度:预处理$O(n)$,查询(线段树维护)$O(\log^2$ $n)$
④轻重链剖分的具体实现

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=100005; 6 int p[N],noww[2*N],goal[2*N]; 7 int anc[N],siz[N],dep[N],top[N],imp[N],dfn[N]; 8 long long num[N],nmb[N],val[4*N],laz[4*N]; 9 int n,m,r,t1,t2,typ,cnt,tot; 10 long long mod,t3; 11 void link(int f,int t) 12 { 13 noww[++cnt]=p[f]; 14 goal[cnt]=t,p[f]=cnt; 15 } 16 void DFS(int nde,int fth,int dth) 17 { 18 int tmp=0; 19 siz[nde]=1,anc[nde]=fth,dep[nde]=dth; 20 for(int i=p[nde];i;i=noww[i]) 21 if(goal[i]!=fth) 22 { 23 DFS(goal[i],nde,dth+1); 24 siz[nde]+=siz[goal[i]]; 25 if(siz[goal[i]]>tmp) 26 tmp=siz[goal[i]],imp[nde]=goal[i]; 27 } 28 } 29 void mark(int nde,int tpp) 30 { 31 top[nde]=tpp,dfn[nde]=++tot,nmb[tot]=num[nde]; 32 if(imp[nde]) 33 { 34 mark(imp[nde],tpp); 35 for(int i=p[nde];i;i=noww[i]) 36 if(goal[i]!=anc[nde]&&goal[i]!=imp[nde]) 37 mark(goal[i],goal[i]); 38 } 39 } 40 void model(int nde) 41 { 42 val[nde]%=mod,laz[nde]%=mod; 43 } 44 void create(int nde,int l,int r) 45 { 46 if(l==r) 47 val[nde]=nmb[l]; 48 else 49 { 50 int mid=(l+r)/2,ls=2*nde,rs=2*nde+1; 51 create(ls,l,mid),create(rs,mid+1,r); 52 val[nde]=(val[ls]+val[rs])%mod; 53 } 54 } 55 void release(int nde,int l,int r) 56 { 57 if(laz[nde]) 58 { 59 int mid=(l+r)/2,ls=2*nde,rs=2*nde+1; 60 laz[ls]+=laz[nde],laz[rs]+=laz[nde]; 61 val[ls]+=laz[nde]*(mid-l+1),val[rs]+=laz[nde]*(r-mid); 62 model(ls),model(rs),laz[nde]=0; 63 } 64 } 65 void add(int nde,int l,int r,int nl,int nr,long long task) 66 { 67 if(l>nr||r<nl) 68 return ; 69 else if(l>=nl&&r<=nr) 70 val[nde]+=task*(r-l+1)%mod,laz[nde]+=task,model(nde); 71 else 72 { 73 int mid=(l+r)/2,ls=2*nde,rs=2*nde+1; release(nde,l,r); 74 add(ls,l,mid,nl,nr,task),add(rs,mid+1,r,nl,nr,task); 75 val[nde]=(val[ls]+val[rs])%mod; 76 } 77 } 78 long long query(int nde,int l,int r,int nl,int nr) 79 { 80 if(l>nr||r<nl) 81 return 0; 82 else if(l>=nl&&r<=nr) 83 return val[nde]; 84 else 85 { 86 int mid=(l+r)/2,ls=2*nde,rs=2*nde+1; release(nde,l,r); 87 return (query(ls,l,mid,nl,nr)+query(rs,mid+1,r,nl,nr))%mod; 88 } 89 } 90 void chain_add(int x,int y,int v) 91 { 92 while(top[x]!=top[y]) 93 { 94 if(dep[top[x]]<dep[top[y]]) swap(x,y); 95 add(1,1,n,dfn[top[x]],dfn[x],v); x=anc[top[x]]; 96 } 97 if(dep[x]>dep[y]) swap(x,y); 98 add(1,1,n,dfn[x],dfn[y],v); return ; 99 } 100 long long chain_query(int x,int y) 101 { 102 long long ret=0; 103 while(top[x]!=top[y]) 104 { 105 if(dep[top[x]]<dep[top[y]]) swap(x,y); 106 ret+=query(1,1,n,dfn[top[x]],dfn[x]),ret%=mod,x=anc[top[x]]; 107 } 108 if(dep[x]>dep[y]) swap(x,y); 109 return (ret+query(1,1,n,dfn[x],dfn[y]))%mod; 110 } 111 void tree_add(int x,int v) 112 { 113 add(1,1,n,dfn[x],dfn[x]+siz[x]-1,v); 114 } 115 long long tree_query(int x) 116 { 117 return query(1,1,n,dfn[x],dfn[x]+siz[x]-1); 118 } 119 int main () 120 { 121 scanf("%d%d%d%lld",&n,&m,&r,&mod); 122 for(int i=1;i<=n;i++) 123 scanf("%lld",&num[i]),num[i]%=mod; 124 for(int i=1;i<n;i++) 125 { 126 scanf("%d%d",&t1,&t2); 127 link(t1,t2),link(t2,t1); 128 } 129 DFS(r,0,1); mark(r,r); create(1,1,n); 130 while(m--) 131 { 132 scanf("%d",&typ); 133 if(typ==1) 134 scanf("%d%d%lld",&t1,&t2,&t3),chain_add(t1,t2,t3%mod); 135 else if(typ==2) 136 scanf("%d%d",&t1,&t2),printf("%lld\n",chain_query(t1,t2)); 137 else if(typ==3) 138 scanf("%d%lld",&t2,&t3),tree_add(t2,t3%mod); 139 else if(typ==4) 140 scanf("%d",&t2),printf("%lld\n",tree_query(t2)); 141 } 142 return 0; 143 }
-----------------普通的修改/查询↑-------------------LCA↓

1 int LCA(int x,int y) 2 { 3 while(top[x]!=top[y]) 4 { 5 if(dep[top[x]]<dep[top[y]]) 6 swap(x,y); x=anc[top[x]]; 7 } 8 return dep[x]<dep[y]?x:y; 9 }
⑤轻重链剖分的拓展
dsu on tree(CF原文),或者叫树上启发式合并(因为感觉和dsu关系不大),可以在$O(nlog$ $n)$时间内解决子树统计的问题
暴力的做法是走到一个点就把子树DFS修改一遍,然后再DFS一遍撤回修改,再往儿子走
如何优化
对每个点先一个个递归统计轻儿子(然后删掉),之后沿着重儿子往下统计(保留影响),最后把轻儿子的答案加进来
复杂度证明:因为每个节点到根的路径上最多有$\log n$条轻边,所以最多会被暴力$\log n$遍

1 //fafafa? 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=100005; 7 long long xnt[N],ans[N]; 8 int p[N],noww[2*N],goal[2*N]; 9 int val[N],siz[N],imp[N],vis[N]; 10 int n,m,t1,t2,cnt; 11 long long maxx,sum; 12 void link(int f,int t) 13 { 14 noww[++cnt]=p[f]; 15 goal[cnt]=t,p[f]=cnt; 16 } 17 void DFS(int nde,int fth) 18 { 19 int tmp=0; siz[nde]=1; 20 for(int i=p[nde];i;i=noww[i]) 21 if(goal[i]!=fth) 22 { 23 DFS(goal[i],nde); 24 siz[nde]+=siz[goal[i]]; 25 if(siz[goal[i]]>tmp) 26 tmp=siz[goal[i]],imp[nde]=goal[i]; 27 } 28 } 29 void Change(int nde,int fth,int tsk) 30 { 31 int v=val[nde]; xnt[v]+=tsk; 32 if(xnt[v]>=maxx) 33 (xnt[v]>maxx)?maxx=xnt[v],sum=v:sum+=v; 34 for(int i=p[nde];i;i=noww[i]) 35 if(goal[i]!=fth&&!vis[goal[i]]) 36 Change(goal[i],nde,tsk); 37 } 38 void Solve(int nde,int fth,int usd) 39 { 40 for(int i=p[nde];i;i=noww[i]) 41 if(goal[i]!=fth&&goal[i]!=imp[nde]) 42 Solve(goal[i],nde,0); 43 if(imp[nde]) 44 Solve(imp[nde],nde,1),vis[imp[nde]]=true; 45 Change(nde,fth,1),ans[nde]=sum; 46 if(imp[nde]) vis[imp[nde]]=false; 47 if(!usd) Change(nde,fth,-1),maxx=sum=0; 48 } 49 int main() 50 { 51 scanf("%d",&n); 52 for(int i=1;i<=n;i++) 53 scanf("%d",&val[i]); 54 for(int i=1;i<n;i++) 55 { 56 scanf("%d%d",&t1,&t2); 57 link(t1,t2),link(t2,t1); 58 } 59 DFS(1,0); Solve(1,0,0); 60 for(int i=1;i<=n;i++) 61 printf("%lld ",ans[i]); 62 return 0; 63 }
2.长链剖分
①长链剖分是什么
一种树上统计的方法,可以$O(n)$完成一棵子树中以深度为标准的统计
②长链剖分的原理
类似轻重链剖分的,我们定义长链表示从某个点出发到达最深的点的路径,然后一个点在长链的儿子就叫长儿子,其余的儿子叫短儿子
(为什么一说长儿子都觉得很奇怪啊=。=???)
显然长链们互不相交,且恰好覆盖了整棵树
那么考虑如何在一个点的子树中快速进行以深度为标准的统计,其实我说都是暴力你信吗=。=
方法是递归统计每个短儿子,然后直接统计长儿子的信息(这不就是暴力吗=。=)
特别的是我们发现统计长儿子时这些信息的深度恰好都加了$1$,所以直接用指针就可以$O(1)$完成统计
这样下来复杂度就是$O(\sum$ 链长$)$的,即$O(n)$的
当然我估计现在大部分人都没用过指针(也可能只有我没用过,不过自己看博客+玩一玩应该基本的操作还是会的
③长链剖分的复杂度
以深度为下标进行统计时间复杂度$O(n)$,另外还有一个操作是$O(nlog$ $n)$预处理+$O(1)$回答第$k$级祖先,但我觉得没啥用(都有一个$log$了直接倍增大概也差不了多少)
④长链剖分的具体实现
模板题:洛谷3899 谈笑风生

1 #include<cstdio> 2 #include<vector> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=300005; 7 struct a{int id,ds;}; 8 vector<a> qry[N]; 9 int p[N],noww[2*N],goal[2*N]; 10 int siz[N],anc[N],dep[N],imp[N],maxd[N]; 11 long long tmp[N],ans[N]; long long *poi=tmp,*pts[N]; 12 int n,q,t1,t2,cnt; 13 void link(int f,int t) 14 { 15 noww[++cnt]=p[f]; 16 goal[cnt]=t,p[f]=cnt; 17 } 18 void DFS(int nde,int fth) 19 { 20 int tmp=0; 21 siz[nde]=1,anc[nde]=fth; 22 maxd[nde]=dep[nde]=dep[fth]+1; 23 for(int i=p[nde];i;i=noww[i]) 24 if(goal[i]!=fth) 25 { 26 DFS(goal[i],nde); 27 siz[nde]+=siz[goal[i]]; 28 if(maxd[goal[i]]>tmp) 29 tmp=maxd[goal[i]],imp[nde]=goal[i]; 30 } 31 if(imp[nde]) 32 maxd[nde]=maxd[imp[nde]]; 33 } 34 void Getans(int nde) 35 { 36 pts[nde][0]=siz[nde]-1; 37 if(imp[nde]) 38 { 39 pts[imp[nde]]=pts[nde]+1; 40 Getans(imp[nde]); 41 pts[nde][0]+=pts[imp[nde]][0]; 42 } 43 for(int i=p[nde];i;i=noww[i]) 44 if(goal[i]!=anc[nde]&&goal[i]!=imp[nde]) 45 { 46 int tmp=maxd[goal[i]]-dep[goal[i]]+1; 47 pts[goal[i]]=poi,poi+=tmp,Getans(goal[i]); 48 for(int j=1;j<=tmp;j++) 49 pts[nde][j]+=pts[goal[i]][j-1]; 50 pts[nde][0]+=pts[goal[i]][0]; 51 } 52 for(int i=qry[nde].size()-1;~i;i--) 53 { 54 a tmp=qry[nde][i]; 55 long long dis=tmp.ds;int idx=tmp.id; 56 ans[idx]+=min(1ll*dep[nde]-1,dis)*(siz[nde]-1); 57 ans[idx]+=pts[nde][0]-siz[nde]+1; 58 if(dis<maxd[nde]-dep[nde]) ans[idx]-=pts[nde][dis+1]; 59 } 60 } 61 int main() 62 { 63 scanf("%d%d",&n,&q); 64 for(int i=1;i<n;i++) 65 { 66 scanf("%d%d",&t1,&t2); 67 link(t1,t2),link(t2,t1); 68 } 69 for(int i=1;i<=q;i++) 70 { 71 scanf("%d%d",&t1,&t2); 72 qry[t1].push_back((a){i,t2}); 73 } 74 DFS(1,0),pts[1]=poi,poi+=maxd[1],Getans(1); 75 for(int i=1;i<=q;i++) 76 printf("%lld\n",ans[i]); 77 return 0; 78 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号