模板汇总2.3_图论3
1.匈牙利算法
①匈牙利算法能干啥
当然是求二分图最大匹配咯(大雾),不过问题来了——什么是二分图,什么是二分图的匹配,什么又是二分图的最大匹配?我们一个个慢慢写。
(1)什么是二分图
二分图是一种特殊的图。对于一张无向图,如果它的顶点们可分割为两个不相交的子集$S1$和$S2$,并且图中的每条边$(node1,node2)$所关联的两个顶点分别属于这两个不同的顶点集,这张图就是一张二分图。
简单说来,如果你能够把一张无向图里的顶点分成两坨,每一坨中间没有相连的边,这张图就是二分图了。
(2)什么是二分图的(最大)匹配
先普及一些(不管用到用不到的)定义:
1.覆盖:①点覆盖:图$G$的一个点集$v$,使得每一条边至少有一个端点属于$v$。②边覆盖:图$G$的边集的一个子集$e$,使得每一个点都与$e$中的至少一条边关联。
在二分图上,最小点覆盖等于最大匹配,最小边覆盖等于总点数-最大匹配
普遍的,最小/大点覆盖等于全集-最大/小点独立集
2.支配集(一般指点支配集):在一张图$G$的的一个点集$v$里,若这个点集的每个点所有邻点的并恰为这个点集的补集,则称这个点集是图$G$的一个点支配集。
3.独立集:①点独立集:在一张图$G$的的一个点集$v$里,若点集中任两个点间都没有边,则称这个点集是图$G$的一个点独立集。②边独立集:即常说的“匹配”,在图$G$的一个子图$g$里,
若子图$g$中没有任何顶点连接了两条边(亦即没有任何两条边有公共的顶点),则称这张子图$g$是图$G$的一个匹配。
在二分图上,最大独立集等于点数减最大匹配
所有匹配中边数最大的匹配称二分图的最大匹配,每个顶点都和图中某条边相关联的匹配,称二分图的完备匹配。
5.团:图$G$的一个子图$v$,且$v$是一个完全图
最大团等于补图的最大独立集
6.反链:图$G$的一个点集$v$,其中的点两两不可达
Dilworth定理告诉我们,最长/短反链=最小/大链覆盖
②匈牙利算法的原理
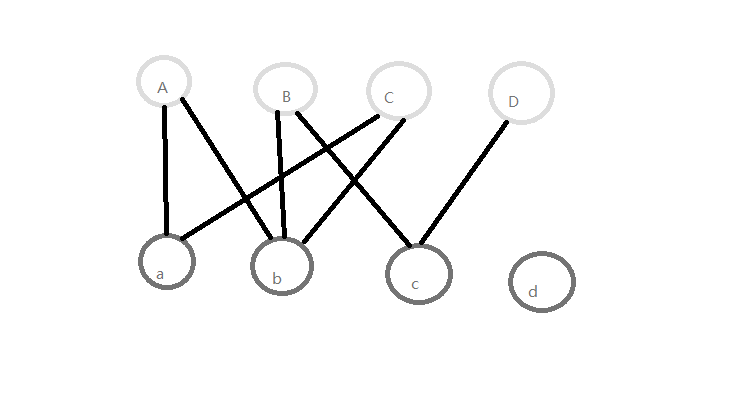
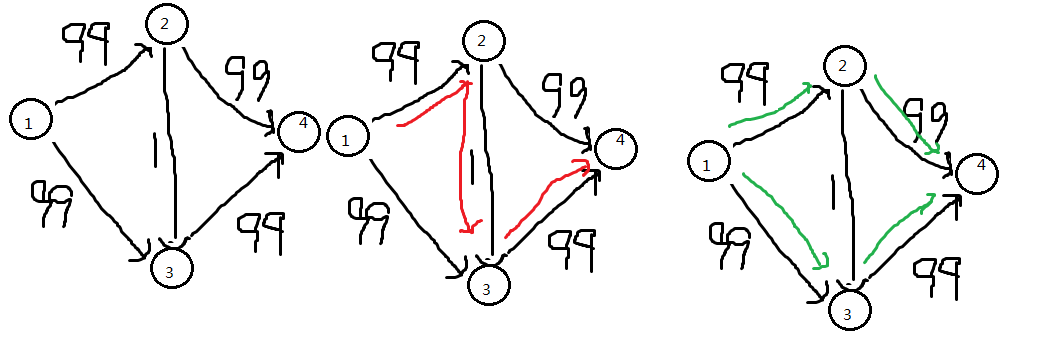
先抓来一张二分图↑(边已经标出)
我们开始尝试寻找最大匹配,按照从左到右的顺序来,我们首先把A与a配对,然后是B与b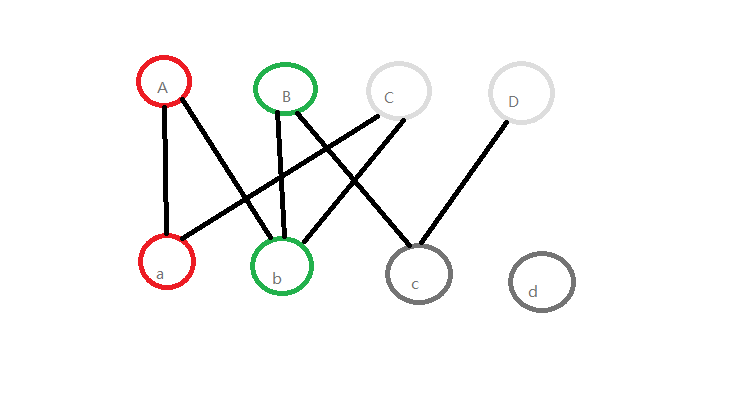
该轮到C了,但是我们发现和C相连的a与b都已经连过了,为了尽可能的满足更♂多的要求,仍然按照顺序,我们先把A与a拆开,尝试给A连下一个(即b),然而b已经和B连上了,于是我们继续把B与b拆开(emmm),发现B可以去和c连,这样一来A与C也就都能配对了,不错。
在代码中,我们用递归实现上述过程:如果一个点还未配对,就让当前点和他配对;如果这个点已经配对,那么如果本来和他配对的点还能找到另一个没人要的点配对,就把这个点给当前点去配对,让原来和他配对的点去和没人要的点配对,而如果本来和他配对的点找不到没人要的点,那就算了。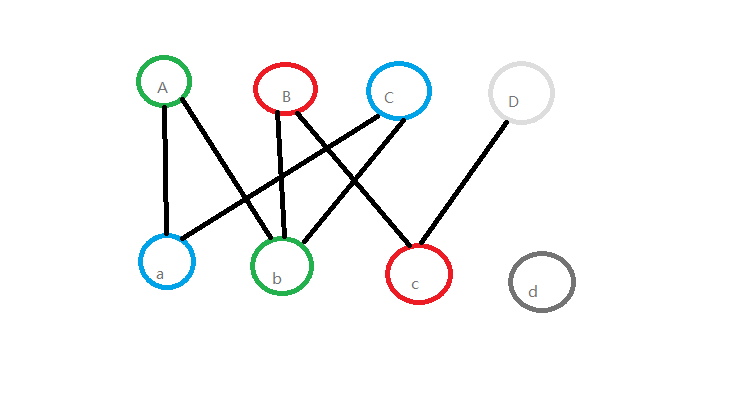
拆开已配对的点尝试为C找配对点↑
重新配对完成↓
最后轮到了D,怎么拆也多不了了,匈牙利算法结束。
③匈牙利算法的时间复杂度
时间复杂度:$O(nm)$
④匈牙利算法的具体实现

1 #include<cstdio> 2 #include<cstring> 3 const int N=1005; 4 bool paired[N][N],judge[N];//邻接矩阵和标记数组 5 int n,m,e,t1,t2,cnt; 6 int match[N];//记录配对 7 bool HM_BGM(int now)//当前尝试为now进行配对 8 { 9 for(int i=1;i<=m;i++)//循环为now找配对 10 if(paired[now][i]&&!judge[i])//这个点和now可以连边且这个点还未被配对 11 { 12 judge[i]=true;//记录这个点被配对 13 if(!match[i]||HM_BGM(match[i]))//如上所述 14 { 15 match[i]=now;//配对 16 return true;//找到了 17 } 18 } 19 return false;//没找到 20 } 21 int main() 22 { 23 scanf("%d%d%d",&n,&m,&e); 24 for(int i=1;i<=e;i++) 25 { 26 scanf("%d%d",&t1,&t2); 27 if(t1<=n&&t2<=m) 28 paired[t1][t2]=true;//邻接矩阵 29 } 30 for(int i=1;i<=n;i++) 31 { 32 memset(judge,false,sizeof judge); 33 cnt+=HM_BGM(i);//记录 34 } 35 printf("%d",cnt); 36 return 0; 37 }
2A.网络最大流之Dinic算法
①什么是网络最大流
还记得$Tarjan$那里说过的流图吗?现在完善一下定义就是了。
一个网络流图是一张满足如下性质的流图
0.每条边有一个最大容量$mf$和当前流量$nf$,你可以把每条边看做一根水管,就是那个字面意思quq
1.一条边的当前流量不能超过它的最大容量,即对于所有的边$edg$有$nf[edg]<=mf[edg]$,这被称为“容量限制”
2.这个可以理解为从一个节点$n1$向另一个节点$n2$流$k$的流量等价于从$n2$向$n1$流$-k$的流量(也许现在看起来这没啥用233),这被称为“反对称性”
3.除了源点和汇点外,对于所有其他节点,入流等于出流。即总流量不会凭空增加或减少,这被称为“流守恒”
网络最大流就是指使得从源点到汇点流量最大的方案
②Dinic求网络最大流的原理
先想朴素做法,我们要引入一个概念:增广路,通俗来说就是一条还能流的路,当不再存在增广路时,则意味着已经找到了最大流,这就是增广路定理
于是我们找出增广路,找到了就流过去$^{*_1}$...
(*1:具体的“找”和“流”一会有详细解释,我们先假设我们能做到这两件事)
就错了。。。因为可能这条路径堵住了其他更好的方案,我们要给算法一个“反悔”的机会,就像匈牙利算法那样$^{*_2}$。怎么反悔呢?我们要连一条容量为$0$的反向边,容量为$0$是为了保证只是反悔而不凭空增大流量。然后每次流的时候在反向边上退流(加上流量)
(*2:事实上Dinic最大流通过适当的建图可以跑二分图匹配,同时效率还高于匈牙利算法)
那连完反向边之后呢?我们该找增广路了,但是因为有流量限制,我们怎么知道每次从源点放多少流出去呢?于是乎我们每次BFS一遍找出路径上最小的流量不为零的边,用它增广一遍,然后再来一遍,再增广一遍......直到搜不到了就找到最大流— —分析一下复杂度:我们最多增广$nm$次,每次增广需要BFS一次$O(n+m)$,总复杂度是$O(nm^2)$,这就是EK算法
好像效率有点低,怎么破呢?Dinic算法利用分层图来进行优化:每次从源点依据残余网络跑BFS,统计每个点的深度。然后进行在增广时严格保证每次由$depth=k$的点流向$depth=k+1$的点。这样去除了同层以及低向高的流之后,不断地BFS分层->DFS增广就能找到最大流,复杂度就变成了我不会证的$O(n^2m)$(=。=???)
③Dinic求网络最大流的时间复杂度
时间复杂度:$O(n^2m)$
④Dinic求网络最大流的具体实现
(下为luogu p2774 方格取数的代码)

1 #include<queue> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=105,inf=233333333; 7 int p[N*N],noww[10*N*N],goal[10*N*N],flow[10*N*N]; 8 int mapp[N][N],dep[N*N]; 9 int n,m,cnt=1,all,tot,maxx,S,T; 10 queue<int> qs; 11 int tonum(int xx,int yy) 12 { 13 return (xx-1)*m+yy; 14 } 15 void link(int f,int t,int v) 16 { 17 noww[++cnt]=p[f],p[f]=cnt,goal[cnt]=t,flow[cnt]=v; 18 noww[++cnt]=p[t],p[t]=cnt,goal[cnt]=f,flow[cnt]=0; 19 } 20 bool layer(int s,int t) 21 { 22 memset(dep,0,sizeof dep); 23 dep[s]=1,qs.push(s); 24 while(!qs.empty()) 25 { 26 int tn=qs.front(); qs.pop(); 27 for(int i=p[tn];i;i=noww[i]) 28 if(!dep[goal[i]]&&flow[i]) 29 dep[goal[i]]=dep[tn]+1,qs.push(goal[i]); 30 } 31 return dep[t]; 32 } 33 int augment(int x,int t,int d) 34 { 35 int tmp; if(x==t) return d; 36 for(int i=p[x];i;i=noww[i]) 37 if(dep[goal[i]]==dep[x]+1&&flow[i]) 38 if(tmp=augment(goal[i],t,min(d,flow[i]))) 39 {flow[i]-=tmp,flow[i^1]+=tmp; return tmp;} 40 return 0; 41 } 42 void Dinic(int s,int t) 43 { 44 int tmp=0; 45 while(layer(s,t)) 46 while(true) 47 { 48 tmp=augment(s,t,inf); 49 if(!tmp) break; maxx+=tmp; 50 } 51 } 52 int main () 53 { 54 scanf("%d%d",&n,&m); 55 T=n*m+1; 56 for(int i=1;i<=n;i++) 57 for(int j=1;j<=m;j++) 58 scanf("%d",&mapp[i][j]),tot+=mapp[i][j]; 59 for(int i=1;i<=n;i++) 60 for(int j=1;j<=m;j++) 61 if(!((i^j)&1)) 62 { 63 link(S,tonum(i,j),mapp[i][j]); 64 if(i>1) link(tonum(i,j),tonum(i-1,j),inf); 65 if(i<n) link(tonum(i,j),tonum(i+1,j),inf); 66 if(j>1) link(tonum(i,j),tonum(i,j-1),inf); 67 if(j<m) link(tonum(i,j),tonum(i,j+1),inf); 68 } 69 else link(tonum(i,j),T,mapp[i][j]); 70 Dinic(S,T); printf("%d",tot-maxx); 71 return 0; 72 }
⑤网络流(含费用流)的一些技巧
先说建图,建图才是网络流题目的核心嘛=。=
基本的建图思想:流量代表可行性,费用代表代价(意会一下)
可以先暴力建图,然后再考虑优化,常见的优化建图:“超级点”,等价替代
拆点是个很有用的技巧,记得想想
二分图是非常有用的性质,如果能保证这个性质就可以分左右部点,然后一般题就做完了(甚至还有四染色的题目)
注意利用网络流本身的性质,比如费用流是先保证满流可以用来保证合法,可以用流量作为选取的限制等
然后是对应的一些问题
下凸函数可以跑费用流,因为两者都是越多越大(意会两下)
需要取舍的问题考虑最小割
⑥各种各样的网络流经典问题/模型(各种各样的)
最小割
等于最大流,经常搭配一个东西:平面图最小割等于其对偶图最短路,再具体一些的可以看论文
对偶图的起点终点怎么分?从原源点到原汇点连一条边,然后外部被分开的两半就是对偶图的起点和终点
最大权闭合子图
源点向所有正权点连边,所有负权点向汇点连边,这两个流量是点权绝对值。对于每条边$(x,y)$从$x$向$y$连边,流量为正无穷。答案是正点权和-最小割。
无源汇上下界可行流
要对每个点保证入流等于出流
先假装所有边都流了下限满足下界这个限制,然后用上界-下界构造出残量网络
现在可能流量不守恒,开始修流。设$dif[i]=\sum$入流下界-$\sum$出流下界,新建源点和汇点搞出一张新图,对于$dif[i]>0$的点从源点向$i$连$dif[i]$的边,$dif[i]<0$的点向汇点连$abs(dif[i])$的边,然后看是否满流
有源汇上下界可行流
为了转化为上面那个问题,先从汇点向源点连一条流量为$(0,inf)$的边,于是变成了无源汇上下界可行流
这篇博客写的挺好的
费用如何处理?
把每条边的下界乘费用先加进去,然后在新图上跑最小费用最大流
一个技巧:如何只让一段$l->r$的流量增大?
从$r$连回$l$即可
有源汇上下界最大流
有源汇上下界可行流的基础上删掉新加的源汇点和原汇点到原源点的边,再在残量网络上跑一遍最大流,最终的答案再加上这个新增广出来的流量即可
有源汇上下界最小流
有源汇上下界可行流的基础上不加汇点到源点的边,先跑一次新源点到新汇点的最大流,再加上汇点到源点的边$(0,inf)$再跑一次新源点到新汇点的最大流,这时汇点到源点的流量就是答案
放一道有源汇上下界最小费用可行流的代码
虽然因为年代久远,编题人不负责等等原因有很多锅,但是有些题还是很不错的
还有这个东西全名是网络流与线性规划24题
把这两个东西放在一起是因为很多时候网络流都能解线性规划,但是有些时候其他算法也可以解决线性规划
说在前面:拆点能解决很多问题
①餐巾计划
拆点网络流好题 Good Blog
然而如果你脑补一下(显然可以一开始把所有要买的餐巾全买了):餐巾太少不够用,餐巾太多会浪费,于是你瞎猜这是个单峰函数,写个三分+check就过了
(你妈的,为什么
②CTSC1999 家园
拆点网络流给题,按阶段建图 建图相当暴力......Good Blog
③飞行员配对
一般通过二分图匹配
④软件补丁
状压+BellmanFord转移
⑤试题库
一般通过网络流建图
⑥太空飞行计划
一般通过最大权闭合子图
⑦最小路径覆盖
一般通过二分图匹配(原因可以看上面的二分图那里有写)
⑧魔术球
暴力尝试个数,每次把相加能构成完全平方数的数从小到大连边
也可以找规律+贪心,但是这个贪心的正确性不显然,这里就不放链接了(虽然确实这个做法更优秀)
⑨最长不降子序列
拼合题
先DP,然后从长度为s的最长不降子序列的开头结尾分别连到源汇点,按大小关系再从前往后连边,为了限制总数再加一对超级源汇
⑩航空路线
一般通过拆点网络流(拆点限制流量)
⑪方格取数
一般通过棋盘二分图模型+最小割
⑫机器人路径规划
只有猫老师在15年给出了一个n^6的DP做法,可以上网搜
⑬圆桌
一般通过网络流建图
同时被贪心踩
⑭骑士共存
BZOJ4808马 的 弱弱化版
一般通过二分图匹配(因为是求最大独立集,原因可以看上面的二分图那里)
⑮火星探险
先让一个最多,其次再让一个最多,费用流√
限制次数,拆点√
输出方案,DFS√
做得渐渐有了套路了
⑯区间k覆盖
前几天,考板子,我不会,被吊打
(离散化不提)
把点从头到尾串起来,每个点向右边的点连容量k费用零的边,每个区间的左端点向右端点连容量1费用负长度的边,跑最小费用最大流
⑰平面线段k覆盖
因为有竖着的直线,不能直接抄上面那个
拆点,每个点拆成前后两个点应付上面那种情况
⑱汽车加油行驶
分层图最短路
⑲孤岛营救
状压钥匙,跑BFS
⑳深海机器人
火星探险弱化版
(21)数字梯形
一般通过套路题(指拆点限流)
(22)分配
一般通过费用流
(23)运输
一般通过费用流
(24)负载平衡
抱歉这个完全没有费用流的意义,直接贪心搞中位数就好
3.费用流
①这是啥
给你张流图,每条边再多一个费用$f$,表示每单位的流量花费$f$,求最小花费下的最大流
②怎么做
把EK的BFS换成最短路算法,因为一般是有负权边的我们一般用SPFA,没有负权边当然上Dijkstra+堆优化(Dijkstra通过某种科技也可以用来跑有负权边的费用流,但是蒟蒻博主不会),然后每次记录一下前驱节点和边,跑到汇点就一路反着增广回去
③时间复杂度
$O(n^2m^2)$
④具体实现

1 #include<queue> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=10005,M=100005,inf=1e9; 7 int n,m,s,t,t1,t2,t3,t4,id,cnt,maxf,minc; 8 int noww[2*M],goal[2*M],flow[2*M],cost[2*M]; 9 int p[N],mflw[N],mcst[N],queu[N],pren[N],pree[N]; 10 queue<int> qs; 11 void link(int f,int t,int v,int c) 12 { 13 noww[++cnt]=p[f],p[f]=cnt; 14 goal[cnt]=t,flow[cnt]=v,cost[cnt]=c; 15 } 16 void Init(int st,int ed) 17 { 18 memset(mflw,0x3f,sizeof mflw); 19 memset(mcst,0x3f,sizeof mcst); 20 memset(queu,0,sizeof queu),pren[ed]=-1; 21 qs.push(st),queu[st]=true,mcst[st]=0; 22 } 23 bool SP(int st,int ed) 24 { 25 Init(st,ed); 26 while(!qs.empty()) 27 { 28 int tn=qs.front(); 29 qs.pop(); queu[tn]=false; 30 for(int i=p[tn],g;i;i=noww[i]) 31 if(mcst[g=goal[i]]>mcst[tn]+cost[i]&&flow[i]) 32 { 33 pren[g]=tn,pree[g]=i; 34 mcst[g]=mcst[tn]+cost[i]; 35 mflw[g]=min(mflw[tn],flow[i]); 36 if(!queu[g]) qs.push(g),queu[g]=true; 37 } 38 } 39 return ~pren[ed]; 40 } 41 void MCMF(int st,int ed) 42 { 43 while(SP(st,ed)) 44 { 45 maxf+=mflw[ed],id=ed; 46 minc+=mflw[ed]*mcst[ed]; 47 while(id!=st) 48 { 49 flow[pree[id]]-=mflw[ed]; 50 flow[pree[id]^1]+=mflw[ed]; 51 id=pren[id]; 52 } 53 } 54 } 55 int main () 56 { 57 scanf("%d%d%d%d",&n,&m,&s,&t),cnt=1; 58 for(int i=1;i<=m;i++) 59 { 60 scanf("%d%d%d%d",&t1,&t2,&t3,&t4); 61 link(t1,t2,t3,t4),link(t2,t1,0,-t4); 62 } 63 MCMF(s,t),printf("%d %d",maxf,minc); 64 return 0; 65 }
⑤从上面接下来的扩展
有源汇上下界费用流
有源汇上下界可行流的基础上把原图中的边费用*下界先统计起来,费用不变,其他边费用为零,最后从新源点到新汇点正常跑费用流
4.最小割树
①什么是最小鸽割树
最小割们形成的一棵树,允许你(在$O(n*$网络流$)$)的预处理之后$O(1)$回答两点间最小割
(说实话感觉非常不普适
②怎么建最小割树
分治
任取两点作为源汇点,跑一次最小割,把源汇点以最小割加入最小割树。
在原点开始在不越过满流边的前提下遍历当前的图,这样图会被割集分裂成两个部分,递归这两个部分
注意每次的最小割都是针对整张图跑出来的
最终两点间的最小割就是最小割树上两点路径上的最小值
③建最小割树的时间复杂度
如果你使用一般的网络流算法(指Dinic或ISAP)复杂度上界是$O(n^3m)$,当然网络流都跑不满(笑
④具体实现

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=1000,M=20000,inf=1e9; 6 int pp[N],dep[N],que[N],bel[N],mem[N],ans[N][N]; 7 int p[N],noww[M],goal[M],flow[M],flw[M]; 8 int P[N],Noww[M],Goal[M],Val[M],vis[N]; 9 int n,m,f,b,T,t1,t2,t3,nw,cnt,Cnt,tot; 10 void Link(int f,int t,int v) 11 { 12 noww[++cnt]=p[f],p[f]=cnt; 13 goal[cnt]=t,flow[cnt]=v; 14 noww[++cnt]=p[t],p[t]=cnt; 15 goal[cnt]=f,flow[cnt]=v; 16 } 17 void Linka(int f,int t,int v) 18 { 19 Noww[++Cnt]=P[f],P[f]=Cnt; 20 Goal[Cnt]=t,Val[Cnt]=v; 21 Noww[++Cnt]=P[t],P[t]=Cnt; 22 Goal[Cnt]=f,Val[Cnt]=v; 23 } 24 void Init(int st) 25 { 26 for(int i=1;i<=n;i++) pp[i]=p[i]; 27 memset(dep,-1,sizeof dep); 28 que[f=b=0]=st,dep[st]=0; 29 } 30 bool Layering(int st,int ed) 31 { 32 Init(st); 33 while(f<=b) 34 { 35 int tn=que[f++]; 36 for(int i=pp[tn];i;i=noww[i]) 37 if(dep[goal[i]]==-1&&flow[i]) 38 dep[goal[i]]=dep[tn]+1,que[++b]=goal[i]; 39 } 40 return ~dep[ed]; 41 } 42 int Augmenting(int nd,int ed,int mn) 43 { 44 if(nd==ed||!mn) return mn; 45 int tmp,tep=0; 46 for(int i=pp[nd];i;i=noww[i]) 47 { 48 pp[nd]=i; 49 if(dep[goal[i]]==dep[nd]+1) 50 if(tmp=Augmenting(goal[i],ed,min(mn,flow[i]))) 51 { 52 flow[i]-=tmp,mn-=tmp; 53 flow[i^1]+=tmp,tep+=tmp; 54 if(!mn) break; 55 } 56 } 57 return tep; 58 } 59 int Dinic_Maxflow(int st,int ed) 60 { 61 int ret=0; 62 for(int i=2;i<=cnt;i++) 63 flow[i]=flw[i]; 64 while(Layering(st,ed)) 65 ret+=Augmenting(st,ed,inf); 66 return ret; 67 } 68 void DFS(int nde) 69 { 70 vis[nde]=tot; 71 for(int i=p[nde];i;i=noww[i]) 72 if(vis[goal[i]]!=tot&&flow[i]) DFS(goal[i]); 73 } 74 void Create(int l,int r) 75 { 76 if(l>=r) return ; 77 int xx=bel[l],yy=bel[l+1]; 78 int minc=Dinic_Maxflow(xx,yy); 79 Linka(xx,yy,minc),tot++,DFS(xx); 80 int lp=l,rp=r; 81 for(int i=l;i<=r;i++) 82 (vis[bel[i]]==tot)? 83 mem[lp++]=bel[i]:mem[rp--]=bel[i]; 84 for(int i=l;i<=r;i++) bel[i]=mem[i]; 85 Create(l,lp-1),Create(rp+1,r); 86 } 87 void Getcut(int nde,int fth) 88 { 89 for(int i=P[nde];i;i=Noww[i]) 90 if(Goal[i]!=fth) 91 ans[nw][Goal[i]]=min(ans[nw][nde],Val[i]),Getcut(Goal[i],nde); 92 } 93 int main() 94 { 95 scanf("%d%d",&n,&m),cnt=1; 96 for(int i=1;i<=m;i++) 97 { 98 scanf("%d%d%d",&t1,&t2,&t3); 99 flw[cnt+1]=flw[cnt+2]=t3,Link(t1,t2,t3); 100 } 101 for(int i=1;i<=n;i++) bel[i]=i; Create(1,n); 102 for(int i=1;i<=n;i++) nw=i,ans[nw][nw]=inf,Getcut(i,0); 103 scanf("%d",&T); 104 while(T--) 105 { 106 scanf("%d%d",&t1,&t2); 107 printf("%d\n",ans[t1][t2]); 108 } 109 return 0; 110 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号