模板汇总2.2_图论2
1.Tarjan_SCC[强连通分量(+缩点)]
special:什么是Tarjan?
说“什么是Tarjan”不好,Tarjan全名Robert Tarjan,是一位计算机学家,发明/提出了许多(神奇)的算法和数据结构,比如LCA(最近公共祖先),SCC(Strongly Connected Component,即强连通分量,下文用Tarjan_SCC代替标题),还有LCT(Link Cut Tree,动态树),斐波那契堆等。

--------------------------------Robert Tarjan(老爷爷是40后)---------------------------------
①强连通分量是啥
说到强连通分量要先说强连通图。对于一张有向图,若其中任意两个节点$node1$和$node2$间既存在从$node1$到$node2$的路径,也存在$node2$到$node1$的路径,我们就称这张图是一张“强连通图”,同时我们称一张有向图的极大强连通子图为强连通分量。
②Tarjan算法求强连通分量的原理
说到这个要先说两个定义:流图和流图的搜索树。(淦)
什么是流图?对于一张有向图,若从一点出发能到达这张图中的所有点,则称这张图是一张流图,这个点称流图的源点。类似的,若从任意一点出发都能到达一点,称这个点为流图的汇点。(先给网络流打个基础)
(引自lyd前辈的蓝书)从一张流图的源点进行深度优先遍历,过程中各点间第一次访问所经的边会构成一棵以源点为根的搜索树,这就是流图的搜索树,我们将构成流图的边($x->y$)分为四种:树枝边,前向边,后向边和横叉边。
树枝边:搜索树中的边,即$x$是$y$的爸爸
前向边:$x$是$y$的祖宗
后向边:$y$是$x$的祖宗
横叉边:除了上面三种边都是横叉边**(显然它们满足$dfn[y]<dfn[x]$)**
然后问题来了:$dfn$又是啥
我们在深度优先遍历中,按照每个节点第一次被访问的时间顺序,将$1->N$的整数标记赋给这些点,这些标记就是$dfn$,时间戳。
回到Tarjan_SCC的原理,我们~~胡乱~~分析,很容易发现每个环都是一张强连通图,因此,Tarjan_SCC的基本思路就是对于每个节点寻找能与它构成环的所有节点。
对于构成一个环,后向边显然十分有用,横叉边也可能有贡献。我们维护一个栈,将每个节点$n$的祖宗$fa(n)$和已经被访问且能到达$fa(n)$的点扔进去。若$fn$是$n$的祖宗之一,且$n->fn$有一条后向边,$n$和$fn$显然在一个环里;若$nfn$能到达$fn$,且$n->nfn$有一条横叉边,$n,fn,nfn$显然在一个环里。由此我们又引入一个叫回溯值$low$的东西
放张图压压惊↑
回溯值$low[n]$的定义是:一个在栈中且被一条搜索树中的边指向的点n的最小时间戳,我们先说如何计算$low[n]$。
一个节点$n$被首次访问时,把它丢进栈里,令$low[n]=dfn[n]$。接下来扫描从$n$出发的边,对于每个$goal[i]$分类讨论,由$low$的定义有:
(1)$goal[i]$被访问过而且还在栈里歇着呢,则显然有
$low[n]=min(low[n],dfn[goal[i]]$ (或$low[goal[i]]$*))
(2)goal[i]还没被访问过,于是搜索树会扩展出一条树枝边,先递归到Tarjan_SCC(goal[i]),最后再返回$low[n]=min(low[n],low[goal[i]])$
(* :经实践和理论证明,这两种写法在求SCC时等价,在此不赘述~~其实是懒~~,但在Tarjan求割点时另有不同,下面有写)
最后是喜闻乐见的结论了:对于一个节点n,若有$dfn[n]==low[n]$,则栈中从x往上的所有节点构成一个强连通分量。我们向上看:
“横叉边:除了上面三种边都是横叉边**(显然它们满足$dfn[y]<dfn[x]$)** ”
因此这些节点不会指向未到达的节点。又根据$dfn$和$low$的定义,它们构成一个强连通分量
③Tarjan算法求强连通分量的时间复杂度
时间复杂度:$O(n+m)$
④Tarjan算法求强连通分量的具体实现
上面讲的差不多了叭

1 #include<stack> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=100005,M=200005; 7 int dfn[N],low[N],col[N]; 8 int noww[M],goal[M],p[N]; 9 int n,m,cnt,tot,c,t1,t2; 10 stack<int> st; 11 bool ins[N]; 12 void link(int f,int t) 13 { 14 noww[++cnt]=p[f]; 15 goal[cnt]=t,p[f]=cnt; 16 } 17 void Tarjan_SCC(int nde) 18 { 19 dfn[nde]=low[nde]=++tot; 20 st.push(nde);ins[nde]=true; 21 for(int i=p[nde];i;i=noww[i]) 22 if(!dfn[goal[i]]) 23 Tarjan_SCC(goal[i]),low[nde]=min(low[nde],low[goal[i]]); 24 else if(ins[goal[i]]) 25 low[nde]=min(low[nde],low[goal[i]]); 26 if(dfn[nde]==low[nde]) 27 { 28 int tmp;c++; 29 do 30 { 31 tmp=st.top(),st.pop(); 32 ins[tmp]=false,col[tmp]=c; 33 }while(nde!=tmp); 34 } 35 } 36 int main () 37 { 38 scanf("%d%d",&n,&m); 39 for(int i=1;i<=m;i++) 40 { 41 scanf("%d%d",&t1,&t2); 42 link(t1,t2); 43 } 44 for(int i=1;i<=n;i++) 45 if(!dfn[i]) Tarjan_SCC(i); 46 return 0; 47 }
1*.基于Tarjan_SCC求割点(或一并求点双联通分量)/割边(或一并求边双联通分量)
①原理及时间复杂度
两个算法都基本与Tarjan_SCC相同,不过它们都是无向图上的算法,主要变化是在扩展搜索树时进行判断。我们重新定义回溯值$low$为满足如下描述的节点的时间戳的最小值:
1.节点在搜索树中
或
2.由此节点经一条非搜索树边能到达搜索树
由此,割点$c$与割边$(u,v)$的判定法则分别为:
割点:当且仅当搜索树上存在一个$c$的儿子$soc$,满足$dfn[c]<=low[soc]$
特别的,在$c$为根节点时,有至少两个$soc$满足上述条件时才可判定$c$为割点
割边:$u,v$都是搜索树上的点,且$v$是$u$的儿子,并满足$dfn[u]<low[v]$
(注意两者的边界条件)
感性证明一波:
以割点为例,满足该条件说明从$soc$出发不经过不经过$c$无法到达比$c$更早被搜到的节点,所以去除$c$则会使$soc$所在的一块与$c$所在的一块断成两个联通块,emmm大概就是这样
时间复杂度 $O(n+m)$
我们还要说一说点双联通分量(PBC,Point Biconnected Component)和边双联通分量(EBC,Edge Biconnected Component),它们的定义分别是这样的:
对于一张无向图,若其中任意一个节点都可以经过点/边不重复的两条路径到达任意另一个节点,就称这张图是一个点/边双联通的图,一张无向图的极大点/边双连通子图称为点/边双联通分量
根据定义可以看出边双联通分量是“包含”于点双联通分量的(点双一定是边双,反过来就不一定了),我们经常通过“8”字图判断题目要求的是点双还是边双,就像这样:
(“8”字图是边双而不是点双)
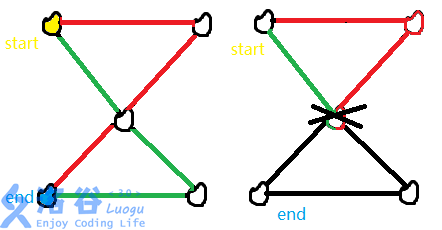
它们都可以在求割点/边时顺带求出来
②求割点/边的具体实现
(Upd on 2019.2.15:边双一定修
割点+点双+圆方树:

1 #include<queue> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=200005,M=400005; 7 int n,m,r,c,t1,t2,cnt,Cnt,tot,top; 8 int dfn[N],low[N],col[N],isc[N],stk[N]; 9 int p[N],noww[M],goal[M],P[N],Noww[M],Goal[M]; 10 vector<int> ve[N]; vector<int> ::iterator it; 11 void Link(int f,int t) 12 { 13 noww[++cnt]=p[f]; 14 goal[cnt]=t,p[f]=cnt; 15 noww[++cnt]=p[t]; 16 goal[cnt]=f,p[t]=cnt; 17 } 18 void Linka(int f,int t) 19 { 20 Noww[++Cnt]=P[f]; 21 Goal[Cnt]=t,P[f]=Cnt; 22 Noww[++Cnt]=P[t]; 23 Goal[Cnt]=f,P[t]=Cnt; 24 } 25 void Tarjan_PBC(int nde) 26 { 27 int tep=0; stk[++top]=nde; 28 dfn[nde]=low[nde]=++tot; 29 for(int i=p[nde];i;i=noww[i]) 30 if(!dfn[goal[i]]) 31 { 32 Tarjan_PBC(goal[i]); 33 low[nde]=min(low[nde],low[goal[i]]); 34 if(dfn[nde]<=low[goal[i]]) 35 { 36 if(nde!=r||++tep>1) isc[nde]=true; 37 int tmp; c++; 38 do 39 { 40 tmp=stk[top--],col[tmp]=c; 41 ve[c].push_back(tmp); 42 }while(tmp!=goal[i]); 43 ve[c].push_back(nde); 44 } 45 } 46 else low[nde]=min(low[nde],dfn[goal[i]]); 47 } 48 int main() 49 { 50 scanf("%d%d",&n,&m); 51 for(int i=1;i<=m;i++) 52 scanf("%d%d",&t1,&t2),Link(t1,t2); 53 for(int i=1;i<=n;i++) 54 if(!dfn[i]) r=i,Tarjan_PBC(i); 55 for(int i=1;i<=c;i++) 56 for(it=ve[i].begin();it!=ve[i].end();it++) 57 Linka(n+i,*it); 58 return 0; 59 }
割边+边双:

1 #include<cstdio> 2 #include<vector> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=100005,M=1000005; 7 int dfn[N],low[N],col[N],isc[M]; 8 int p[N],noww[M],goal[M]; 9 int n,m,t1,t2,cnt,tot,dcc; 10 vector<int> DCC[N]; 11 void Link(int f,int t) 12 { 13 noww[++cnt]=p[f]; 14 goal[cnt]=t,p[f]=cnt; 15 noww[++cnt]=p[t]; 16 goal[cnt]=f,p[t]=cnt; 17 } 18 void Tarjan_DCC(int nde,int edg) 19 { 20 dfn[nde]=low[nde]=++tot; 21 for(int i=p[nde];i;i=noww[i]) 22 { 23 if(!dfn[goal[i]]) 24 { 25 Tarjan_DCC(goal[i],i); 26 low[nde]=min(low[nde],low[goal[i]]); 27 if(low[goal[i]]>dfn[nde]) 28 isc[i]=isc[i^1]=true; 29 } 30 else if(i!=(edg^1)) 31 low[nde]=min(low[nde],dfn[goal[i]]); 32 } 33 } 34 void DFS(int nde) 35 { 36 col[nde]=dcc; 37 for(int i=p[nde];i;i=noww[i]) 38 if(!isc[i]&&!col[goal[i]]) DFS(goal[i]); 39 } 40 int main() 41 { 42 scanf("%d%d",&n,&m),cnt=1; 43 for(int i=1;i<=m;i++) 44 scanf("%d%d",&t1,&t2),Link(t1,t2); 45 for(int i=1;i<=n;i++) 46 if(!dfn[i]) Tarjan_DCC(i,0); 47 for(int i=1;i<=n;i++) 48 if(!col[i]) dcc++,DFS(i); 49 return 0; 50 }
③一些更高级的东西
上面说的那个圆方树是什么?
我们把图中原有的点看做圆点,然后每个点双新建一个方点在新图中把点双中的点连过去
一些性质:1.树上不存在“圆圆边”和“方方边” 2.每一个方点对应一个点双联通分量 3.方点的点度是点双联通分量的大小。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号