模板汇总1.2_数据结构2
1.平衡树-树堆与无旋树堆
①平衡树是啥,树堆和无旋树堆又是啥?
平衡树,顾名思义就是长得“平衡”的树,即期望树高在log级别的二叉搜索树(这样每次操作才是log的)
Treap是一种平衡树,叫做“树堆”(tree-heap)。Treap的每个节点会随机分配一个优先级,再根据这个优先级建立一个满足堆性质的平衡树。支持插入/删除(若有多个相同的数,只会删除一个)一个数,查询一个数或它的 排名/前驱/后继
不幸的是Treap的形态随每个点的随机优先级而固定,很不灵活,基本只能作为一棵高效的查找树而无法更灵活地维护信息(下文会详细地说一说)
于是便有了无旋树堆
②两者的原理
我们一开头说了平衡树是“期望树高在log级别的二叉搜索树”,很容易想到为什么平衡树会诞生:普通的二叉搜索树(直接按照定义插入/查找)会被轻松地卡到单次操作O(n)(不停地让你往一边加儿子)。那平衡树如何维持平衡?我见过的主要有两类(当然很可能还有我没见过的,毕竟博主是个鶸嘛=。=):旋转与重构
旋转,就是以某种规则调整节点间的关系以达到平衡,典型的例子有普通树堆和Splay Tree(伸展树)
重构,就是通过把树的一部分重新构造维持平衡,典型的例子有无旋树堆和Scapegoat Tree(替罪羊树)
上文提到,确定了各节点优先级之后,Treap的形态就确定了。所以对于插入一个点,分配优先级之后就考虑用旋转来维护Treap的性质。rotate分为左旋和右旋,我们用图来表示一下rotate。
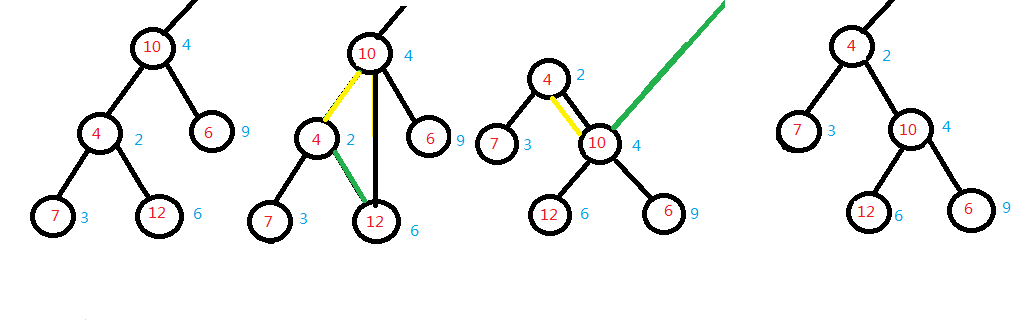
以左旋为例↑
我的写法(其实好久没写了XD,原因下面就知道了)rotate传节点编号和当前节点的左/右儿子(来确定是左旋还是右旋)。定义s为当前节点的l/rs(左/右儿子),我们先把s的与l/rs相反的儿子(即$son[s][l/rson$^1$]$)转给s,再把当前节点转给$son[s][l/rs$^$1]$当儿子。然后更新各节点的size,把s赋给nde传回即可。(手动模拟+图可更好理解,算了我觉得第一次见这个根本不好理解)
1 void rotate(int &nde,int typ) 2 { 3 int tmp=son[nde][typ]; 4 son[nde][typ]=son[tmp][typ^1],son[tmp][typ^1]=nde; 5 siz[nde]=siz[son[nde][0]]+siz[son[nde][1]]+1; nde=tmp; 6 }
有了rotate操作,其他操作就好做多了— —
对于插入一个数,根据二叉搜索树的定义插,然后用旋转维护优先级的堆性质
对于删除一个数,先根据二叉搜索树的定义找到它,然后把它一路旋到叶子级别,删掉,注意更新size
查询就按题意做就好了
然后我们发现Treap的rotate就完全是为了维护其优先级的堆的性质,这也就是其维护平衡的策略,可以证明的是这样的期望树高就是$\log n$的(我怎么会证=。=)
好了又回到了开始的那个问题:Treap的形态被限制死了,根本动不了。假如现在我们要把某个节点拉出来接在另一个节点上,对不起,做不了,Treap就只能让你插/删个数然后查一查
人们一看那不行啊,于是有了两群人(开始扯淡)
一群人说rotate这么灵活的东西全用来维护优先级的堆性质太浪费了,我们不要它维护优先级了,我们就单纯地用rotate来维护平衡— —于是有了Splay(它通过一个叫做“双旋”的操作来维护平衡,但是我觉得写起来太麻烦了,于是有了今天要讲的第二个平衡树)
另一群人说优先级的堆性质能让树高达到期望log干嘛说不用就不用了,我们改进改进方法来维护— —于是有了无旋树堆,我们今天的主角
(扯淡结束)
无旋树堆仍然为每个节点分配一个随机值,不同的是现在维护树形态的方法变成了两个函数:合并与分裂
合并操作用来维护优先级的堆性质,它会将两个节点的子树按照优先级维护成一个堆,具体来说是将一个树作为根,把另一棵树接在某个节点上,这时树高期望是log的,所以复杂度就是log的(即找到那个节点),注意合并操作只负责维护堆的性质,因此在合并时两棵子树必须符合二叉搜索树(或者你想要的)的顺序
分裂操作会将树在某个节点以一个标准断成两棵树,一棵树里的所有节点都满足标准的一侧,另一棵树的所有节点都满足标准的另一侧,因为树高期望是log的,所以找到那个分界点的复杂度就是log的
好了我觉得应该没人听懂,还是讲点好理解的吧=。=
你可以这样理解两个操作:
分裂:按照一个“分界线”把树断成两棵树,比如说我从以$nde$为根的树中拉出来所有不超过$tsk$的的数,就这样写:
1 void Split(int nde,int &x,int &y,int tsk) 2 { 3 if(!nde) x=y=0; 4 else 5 { 6 if(val[nde]<=tsk) 7 x=nde,Split(son[nde][1],son[nde][1],y,tsk); 8 else 9 y=nde,Split(son[nde][0],x,son[nde][0],tsk); 10 Pushup(nde); 11 } 12 }
(pushup是维护size的,然后x,y注意传址)
合并:把两棵树按照优先级的堆的性质并起来,这样树还是平衡的
1 int Merge(int x,int y) 2 { 3 if(!x||!y) return x+y; 4 else if(rnk[x]<=rnk[y]) 5 { 6 son[x][1]=Merge(son[x][1],y); 7 Pushup(x); return x; 8 } 9 else 10 { 11 son[y][0]=Merge(x,son[y][0]); 12 Pushup(y); return y; 13 } 14 }
挺短的吧,这两个操作已经足够了,我们举俩例子
插入一个数$tsk$:首先以$tsk$为标准裂出所有不超过$tsk$的数和所有大于$tsk$的数,然后把$tsk$插在中间,最后依次合起来
1 void Insert(int tsk) 2 { 3 Split(root,x,y,tsk); 4 root=Merge(Merge(x,Create(tsk)),y); 5 }
删除一个数:裂出所有不超过$tsk$的数和所有大于$tsk$的数,在前面那半里再裂出所有不超过$tsk-1$的数,剩下那块就是$tsk$,然后你想删一个数就把剩下那块的堆顶丢掉,想删一种数就丢掉剩下那一整块,最后还是依次合并起来
1 void Delete(int tsk) 2 { 3 Split(root,x,z,tsk),Split(x,x,y,tsk-1); 4 y=Merge(son[y][0],son[y][1]),root=Merge(Merge(x,y),z); 5 }
剩下的看代码吧,都写出来太长了=。=
Merge和Split是无旋树堆的核心操作,也是其所有操作之基础,一定要理解(我觉得是挺好理解的=。=),然后灵活运用这两个操作就够了
③复杂度
时间复杂度每次操作均摊$O(\log n)$
空间在$n$级别
④两者的具体实现

1 #include<cstdio> 2 #include<cstring> 3 #include<cstdlib> 4 #include<algorithm> 5 using namespace std; 6 int val[n],siz[n],son[n][2],rnk[n]; 7 int n,s,t,R,typ,cnt; 8 void rotate(int &nde,int lrs)//最重要的旋转操作 9 { 10 int s=son[nde][lrs];//定儿子 11 son[nde][lrs]=son[s][lrs^1];//“反转” 12 son[s][lrs^1]=nde; 13 siz[nde]=siz[son[nde][0]]+siz[son[nde][1]]+1;//更新siz 14 siz[s]=siz[son[s][0]]+siz[son[s][1]]+1; 15 nde=s;//向下转 16 } 17 void insert_(int &nde,int num)//插入 18 { 19 if(!nde)//建节点 20 { 21 nde=++cnt; 22 siz[nde]=1; 23 val[nde]=num; 24 rnk[nde]=rand(); 25 return ; 26 } 27 siz[nde]++;//别忘了 28 if(num<=val[nde])//根据二叉搜索树性质 29 { 30 insert_(son[nde][0],num); 31 if(rnk[nde]>rnk[son[nde][0]])//维护优先级的堆结构 32 rotate(nde,0); 33 } 34 else 35 { 36 insert_(son[nde][1],num); 37 if(rnk[nde]>rnk[son[nde][1]]) 38 rotate(nde,1); 39 } 40 } 41 void delete_(int &nde,int num)//删除 42 { 43 if(num==val[nde])//找到了 44 if(!(son[nde][0]&&son[nde][1]))//不是“左右双全” 45 { 46 nde=son[nde][0]+son[nde][1];//更新成儿子 47 return; 48 } 49 else if(rnk[son[nde][0]]<=rnk[son[nde][1]])//“左右双全”,根据优先级堆性质,旋转并递归删除 50 { 51 rotate(nde,0); 52 delete_(son[nde][1],num); 53 } 54 else 55 { 56 rotate(nde,1); 57 delete_(son[nde][0],num); 58 } 59 else if(num<val[nde])//二叉搜索树性质 60 delete_(son[nde][0],num); 61 else 62 delete_(son[nde][1],num); 63 siz[nde]=siz[son[nde][0]]+siz[son[nde][1]]+1;//记得更新 64 } 65 int rank_query(int nde,int num)//查询排名 66 { 67 if(!nde)//叶子 68 return 1; 69 if(num<=val[nde])//二叉搜索树性质 70 return rank_query(son[nde][0],num); 71 else 72 return rank_query(son[nde][1],num)+siz[son[nde][0]]+1;//注意size 73 } 74 int num_query(int nde,int num)//对应排名查询数 75 { 76 if(num==siz[son[nde][0]]+1)//没啥可说的 77 return val[nde]; 78 else if(num<=siz[son[nde][0]]) 79 return num_query(son[nde][0],num); 80 else 81 return num_query(son[nde][1],num-siz[son[nde][0]]-1); 82 } 83 int pre_query(int nde,int num)//查询前驱 84 { 85 if(!nde) 86 return -233333333; 87 else if(num<=val[nde])//二叉搜索树性质 88 return pre_query(son[nde][0],num); 89 else 90 return max(val[nde],pre_query(son[nde][1],num)); 91 } 92 int nxt_query(int nde,int num)//查询后继 93 { 94 if(!nde) 95 return 233333333; 96 else if(num>=val[nde])//二叉搜索树性质 97 return nxt_query(son[nde][1],num); 98 else 99 return min(val[nde],nxt_query(son[nde][0],num)); 100 } 101 int main () 102 { 103 srand(20020513);//好像不用srand? 104 scanf("%d",&n); 105 for(int i=1;i<=n;i++) 106 { 107 scanf("%d%d",&typ,&t); 108 if(typ==1) 109 insert_(R,t); 110 else if(typ==2) 111 delete_(R,t); 112 else if(typ==3) 113 printf("%d\n",rank_query(R,t)); 114 else if(typ==4) 115 printf("%d\n",num_query(R,t)); 116 else if(typ==5) 117 printf("%d\n",pre_query(R,t)); 118 else if(typ==6) 119 printf("%d\n",nxt_query(R,t)); 120 } 121 return 0; 122 }

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=100005; 6 int val[N],siz[N],son[N][2],rnk[N]; 7 int n,x,y,z,t1,t2,tot,root; 8 void Pushup(int nde) 9 { 10 siz[nde]=siz[son[nde][0]]+siz[son[nde][1]]+1; 11 } 12 int Create(int tsk) 13 { 14 siz[++tot]=1; 15 val[tot]=tsk; 16 rnk[tot]=rand(); 17 return tot; 18 } 19 int Merge(int x,int y) 20 { 21 if(!x||!y) 22 return x+y; 23 else if(rnk[x]<=rnk[y]) 24 { 25 son[x][1]=Merge(son[x][1],y); 26 Pushup(x); return x; 27 } 28 else 29 { 30 son[y][0]=Merge(x,son[y][0]); 31 Pushup(y); return y; 32 } 33 } 34 void Split(int nde,int &x,int &y,int tsk) 35 { 36 if(!nde) x=y=0; 37 else 38 { 39 if(val[nde]<=tsk) 40 x=nde,Split(son[nde][1],son[nde][1],y,tsk); 41 else 42 y=nde,Split(son[nde][0],x,son[nde][0],tsk); 43 Pushup(nde); 44 } 45 } 46 int Query(int nde,int tsk) 47 { 48 if(tsk<=siz[son[nde][0]]) return Query(son[nde][0],tsk); 49 else if(tsk==siz[son[nde][0]]+1) return nde; 50 else return Query(son[nde][1],tsk-siz[son[nde][0]]-1); 51 } 52 void Insert(int tsk) 53 { 54 Split(root,x,y,tsk); 55 root=Merge(Merge(x,Create(tsk)),y); 56 } 57 void Delete(int tsk) 58 { 59 Split(root,x,z,tsk),Split(x,x,y,tsk-1); 60 y=Merge(son[y][0],son[y][1]),root=Merge(Merge(x,y),z); 61 } 62 int rnk_query(int tsk) 63 { 64 Split(root,x,y,tsk-1); 65 int ret=siz[x]+1; 66 root=Merge(x,y); return ret; 67 } 68 int num_query(int tsk) 69 { 70 return val[Query(root,tsk)]; 71 } 72 int pre_query(int tsk) 73 { 74 Split(root,x,y,tsk-1); 75 int ret=val[Query(x,siz[x])]; 76 root=Merge(x,y); return ret; 77 } 78 int nxt_query(int tsk) 79 { 80 Split(root,x,y,tsk); 81 int ret=val[Query(y,1)]; 82 root=Merge(x,y); return ret; 83 } 84 int main () 85 { 86 srand(20020513); 87 scanf("%d",&n); 88 for(int i=1;i<=n;i++) 89 { 90 scanf("%d%d",&t1,&t2); 91 if(t1==1) Insert(t2); 92 else if(t1==2) Delete(t2); 93 else if(t1==3) printf("%d\n",rnk_query(t2)); 94 else if(t1==4) printf("%d\n",num_query(t2)); 95 else if(t1==5) printf("%d\n",pre_query(t2)); 96 else if(t1==6) printf("%d\n",nxt_query(t2)); 97 } 98 return 0; 99 }
⑤Treap的性质(引自lx大佬的课件)
1.Treap的深度期望为$O(log$ $n)$
2.Treap单次插入引起的旋转次数是期望 $O(1)$
⑥无旋树堆的一些常见操作
还记得(我扯的)那两群人吗,现在说说无旋树堆是怎么维护序列的,其实没啥可说的,就是按size分裂呗,然后树的中序遍历就是原序列。
维护序列很可能需要在裂出的那段区间上打标记,注意在合并和分裂中往儿子走的时候下放标记
然后如何在序列中查找一个数?
按出现次数分配一个权值,然后每次在树上查这个权值的DFS序,具体来说一路走到树根,然后是父亲的右儿子时就加上父亲的左儿子(和父亲),注意自己的左儿子和自己,别漏了
2.可持久化线段树
①可持久化是什么意思
就是“支持查询历史版本”的意思(都是字面意思)
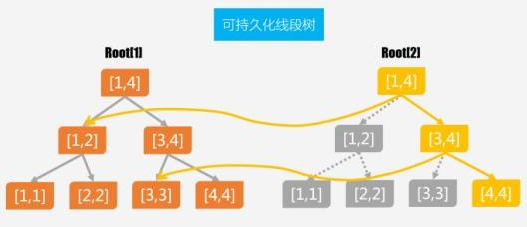
(↑from 百度图片,侵删)
②实现可持久化
因为沙茶博主最近主要在BFS学习,所以不会讲得很深,主要就说说点修的做法
每次修改都重新建一棵
我们以线段树为例,可以发现每次修改涉及到的节点只有log级别,其他的都和之前一样
那么我们不妨动态建立线段树,每次修改后能沿用旧的就沿用,只动态建立新的log级别的节点(以洛谷模板为例)
1 int Insert(int pre,int l,int r,int task) 2 { 3 int nde=++tot; 4 son[nde][0]=son[pre][0]; 5 son[nde][1]=son[pre][1]; 6 cnt[nde]=cnt[pre]+1; 7 if(l<r) 8 { 9 int mid=(l+r)/2; 10 if(task<=mid) 11 son[nde][0]=Insert(son[pre][0],l,mid,task); 12 else 13 son[nde][1]=Insert(son[pre][1],mid+1,r,task); 14 } 15 return nde; 16 }
我们对每个版本保存一个根节点,然后每层插入都是先从上一级那里继承然后向更新的那一侧插入(更新那一侧的节点)
然后就真的没啥了=。=
③复杂度
时间复杂度每次插入$O(\log n)$
空间大概$4*n+2*m\log n$,也可能没这么多?($m$为插入次数)
④具体实现(洛谷模板:可持久化线段树)

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=200005; 6 int n,m,t1,t2,t3,len,tot; 7 int num[N],uni[N],root[N]; 8 int cnt[N*40],son[N*40][2]; 9 int Create(int l,int r) 10 { 11 int nde=++tot; 12 if(l<r) 13 { 14 int mid=(l+r)/2; 15 son[nde][0]=Create(l,mid); 16 son[nde][1]=Create(mid+1,r); 17 } 18 return nde; 19 } 20 int Insert(int pre,int l,int r,int task) 21 { 22 int nde=++tot; 23 son[nde][0]=son[pre][0]; 24 son[nde][1]=son[pre][1]; 25 cnt[nde]=cnt[pre]+1; 26 if(l<r) 27 { 28 int mid=(l+r)/2; 29 if(task<=mid) 30 son[nde][0]=Insert(son[pre][0],l,mid,task); 31 else 32 son[nde][1]=Insert(son[pre][1],mid+1,r,task); 33 } 34 return nde; 35 } 36 int Query(int l,int r,int nl,int nr,int task) 37 { 38 if(l==r) return l; 39 int mid=(l+r)/2,tmp=cnt[son[nr][0]]-cnt[son[nl][0]]; 40 if(task<=tmp) return Query(l,mid,son[nl][0],son[nr][0],task); 41 else return Query(mid+1,r,son[nl][1],son[nr][1],task-tmp); 42 } 43 int main() 44 { 45 scanf("%d%d",&n,&m); 46 for(int i=1;i<=n;i++) 47 scanf("%d",&num[i]),uni[i]=num[i]; 48 sort(uni+1,uni+1+n),len=unique(uni+1,uni+1+n)-uni-1; 49 for(int i=1;i<=n;i++) 50 num[i]=lower_bound(uni+1,uni+1+len,num[i])-uni; 51 root[0]=Create(1,len); 52 for(int i=1;i<=n;i++) 53 root[i]=Insert(root[i-1],1,len,num[i]); 54 while(m--) 55 { 56 scanf("%d%d%d",&t1,&t2,&t3); 57 printf("%d\n",uni[Query(1,len,root[t1-1],root[t2],t3)]); 58 } 59 return 0; 60 }
3.动态树(LCT)
①动态树能干啥
用来维护森林,支持(全部是在线的)删/加边,换根,查询/修改链上信息等操作
②原理
用实链剖分把森林里的每棵树树拆成若干个条链,然后对于每条链用平衡树维护序列
目前只有按深度用Splay维护被Tarjan证明是$O(n\log n)$的复杂度,其他平衡树维护是$O(n\log ^2n)$的。猫老师写过一个跑的和Splay相差无几的FHQ_Treap维护的LCT,是用子树大小做种子维护的,但尚未证明复杂度低于$O(n\log ^2n)$
来看具体操作,下面注意分清这个节点所在的“真实的树”和这个节点所在的Splay
首先是三个“基本函数”,都是(函数名的)字面意思
1 void Pushup(int nde) 2 { 3 xrr[nde]=xrr[son[nde][0]]^xrr[son[nde][1]]^val[nde]; 4 } 5 void Release(int nde) 6 { 7 int &lson=son[nde][0],&rson=son[nde][1]; 8 if(rev[nde]) 9 { 10 rev[lson]^=1,rev[rson]^=1; 11 swap(lson,rson),rev[nde]=0; 12 } 13 } 14 bool Nottop(int nde) 15 { 16 int fa=fth[nde]; 17 return son[fa][0]==nde||son[fa][1]==nde; 18 }
其中$Nottop(nde)$表示判断$nde$是不是不是其所在$Splay$的根节点(雾 ,这仨函数没啥可说的。另外Splay的操作就是在往父节点的父节点上接的时候注意一下有没有这个节点,然后Splay的时候把到当前Splay根节点的标记先下放掉— —用栈实现,这里就不放Splay的部分了。来看LCT的核心操作$Access$,这是LCT所有操作的基础(请不要在意蒟蒻的制杖的嘤文注释)
1 void Access(int nde)//Let the path from the node to real-root be linked 2 { 3 int lst=0,mem=nde;//Important:Rotate the "mem" at last 4 while(nde)//While the node is not the total-root 5 { 6 Splay(nde),son[nde][1]=lst;//Splay it and let the last node be its right-son 7 Pushup(nde),lst=nde,nde=fth[nde];//Pushup the node and jump up to its father 8 } 9 Splay(mem);//Don't forget this 10 }
$Access(nde)$表示将$nde$到当前树的根的路径连成一棵$Splay$,做法是在Splay上不断往上跳,边跳边Splay当前节点同时把上一个节点接在右儿子上,同时要维护好信息。最后再Splay一次这个节点(注意最后这次Splay是一开始记录的节点编号,不然你会得到一个Splay(0)这样的东西)
但是只有$Access$并不能支持链上的操作,因为LCT的Splay是按深度维护的,于是有了LCT的一个重要操作(功能):换根(将节点置为当前树的根),代码很短
1 void Turnroot(int nde) 2 { 3 Access(nde),rev[nde]^=1; 4 }
连到根节点之后左右儿子一翻转整个树的深度就翻转了,很妙
还有另一个重要操作:找(树中的)根,$Access$之后不断跳右儿子,注意找完之后必须Splay保证复杂度
1 int Getroot(int nde) 2 { 3 Access(nde); 4 while(son[nde][0]) 5 nde=son[nde][0]; 6 Splay(nde); 7 return nde; 8 }
于是就能很方便地实现一个有用的操作$Split(x,y)$了,将$x-y$变成一棵Splay,代码也很短(其实都挺短的=。=)
1 void Split(int x,int y) 2 { 3 Turnroot(x),Access(y); 4 }
别的操作都是基于这些操作实现的,看代码吧
③动态树的时间复杂度
一般操作都是$O(\log n)$的
④动态树的具体实现

1 //*你妈的,为什么* (指学了假的LCT) 2 #include<cstdio> 3 #include<cctype> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 const int N=300005; 8 int fth[N],son[N][2],xrr[N]; 9 int val[N],rev[N],stk[N]; 10 int n,m,t1,t2,t3,top;int read() 11 { 12 int ret=0; 13 char ch=getchar(); 14 while(!isdigit(ch)) 15 ch=getchar(); 16 while(isdigit(ch)) 17 ret=(ret<<3)+(ret<<1)+(ch^48),ch=getchar(); 18 return ret; 19 } 20 void write(int x) 21 { 22 if(x>9) write(x/10); 23 putchar(x%10^48); 24 } 25 void Pushup(int nde) 26 { 27 xrr[nde]=xrr[son[nde][0]]^xrr[son[nde][1]]^val[nde]; 28 } 29 void Release(int nde) 30 { 31 if(rev[nde]) 32 { 33 int &lson=son[nde][0],&rson=son[nde][1]; 34 rev[lson]^=1,rev[rson]^=1,rev[nde]^=1; 35 swap(lson,rson); 36 } 37 } 38 bool Nottop(int nde) 39 { 40 int fa=fth[nde]; 41 return son[fa][0]==nde||son[fa][1]==nde; 42 } 43 void Rotate(int nde) 44 { 45 int fa=fth[nde],gr=fth[fa],isl=nde==son[fa][0]; 46 if(Nottop(fa)) son[gr][fa==son[gr][1]]=nde; 47 fth[nde]=gr,fth[fa]=nde,fth[son[nde][isl]]=fa; 48 son[fa][isl^1]=son[nde][isl],son[nde][isl]=fa; 49 Pushup(fa),Pushup(nde); 50 } 51 void Splay(int nde) 52 { 53 stk[top=1]=nde; 54 for(int i=nde;Nottop(i);i=fth[i]) 55 stk[++top]=fth[i]; 56 while(top) Release(stk[top--]); 57 while(Nottop(nde)) 58 { 59 int fa=fth[nde],gr=fth[fa]; 60 if(Nottop(fa)) 61 Rotate(((son[fa][0]==nde)==(son[gr][0]==fa))?fa:nde); 62 Rotate(nde); 63 } 64 Pushup(nde); 65 } 66 void Access(int nde) 67 { 68 int lst=0,mem=nde; 69 while(nde) 70 { 71 Splay(nde),son[nde][1]=lst; 72 Pushup(nde),lst=nde,nde=fth[nde]; 73 } 74 Splay(mem); 75 } 76 void Turnroot(int nde) 77 { 78 Access(nde),rev[nde]^=1; 79 } 80 int Getroot(int nde) 81 { 82 Access(nde); 83 while(son[nde][0]) 84 nde=son[nde][0]; 85 Splay(nde); 86 return nde; 87 } 88 void Split(int x,int y) 89 { 90 Turnroot(x),Access(y); 91 } 92 int Query(int x,int y) 93 { 94 Split(x,y); 95 return xrr[y]; 96 } 97 void Link(int x,int y) 98 { 99 Split(x,y); 100 if(Getroot(y)!=x) fth[x]=y; 101 } 102 void Cut(int x,int y) 103 { 104 Split(x,y); 105 if(son[y][0]==x&&!son[x][1]) 106 fth[x]=son[y][0]=0,Pushup(y); 107 } 108 void Change(int nde,int tsk) 109 { 110 Splay(nde),val[nde]=tsk,Pushup(nde); 111 } 112 int main() 113 { 114 n=read(),m=read(); 115 for(int i=1;i<=n;i++) 116 val[i]=read(),xrr[i]=val[i]; 117 while(m--) 118 { 119 t1=read(),t2=read(),t3=read(); 120 if(!t1) write(Query(t2,t3)),puts(""); 121 else if(t1==1) Link(t2,t3); 122 else if(t1==2) Cut(t2,t3); 123 else Change(t2,t3); 124 } 125 return 0; 126 }
⑤动态树的扩展应用
LCT维护子树信息:记录一个所有轻儿子的信息合并进去,具体来说要改改Access和Link

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=100005,inf=1e9; 6 int fth[N],son[N][2],siz[N],rev[N]; 7 int val[N],aset[N],sizz[N],stk[N]; 8 int n,m,t1,t2,top,xrr; 9 char op[5]; 10 int Finda(int x) 11 { 12 return x==aset[x]?x:aset[x]=Finda(aset[x]); 13 } 14 void Pushup(int nde) 15 { 16 int lson=son[nde][0],rson=son[nde][1]; 17 siz[nde]=siz[lson]+siz[rson]+sizz[nde]+1; 18 } 19 void Release(int nde) 20 { 21 if(rev[nde]) 22 { 23 int &lson=son[nde][0],&rson=son[nde][1]; 24 swap(lson,rson),rev[lson]^=1,rev[rson]^=1,rev[nde]^=1; 25 } 26 } 27 bool Nottop(int nde) 28 { 29 int fa=fth[nde]; 30 return son[fa][0]==nde||son[fa][1]==nde; 31 } 32 void Rotate(int nde) 33 { 34 int fa=fth[nde],gr=fth[fa],isl=nde==son[fa][0]; 35 if(Nottop(fa)) son[gr][fa==son[gr][1]]=nde; 36 fth[nde]=gr,fth[fa]=nde,fth[son[nde][isl]]=fa; 37 son[fa][isl^1]=son[nde][isl],son[nde][isl]=fa; 38 Pushup(fa),Pushup(nde); 39 } 40 void Splay(int nde) 41 { 42 stk[top=1]=nde; 43 for(int i=nde;Nottop(i);i=fth[i]) 44 stk[++top]=fth[i]; 45 while(top) Release(stk[top--]); 46 while(Nottop(nde)) 47 { 48 int fa=fth[nde],gr=fth[fa]; 49 if(Nottop(fa)) 50 Rotate(((son[fa][0]==nde)==(son[gr][0]==fa))?fa:nde); 51 Rotate(nde); 52 } 53 } 54 void Access(int nde) 55 { 56 int mem=nde,lst=0; 57 while(nde) 58 { 59 Splay(nde),sizz[nde]+=siz[son[nde][1]]-siz[lst]; 60 son[nde][1]=lst,Pushup(nde),lst=nde,nde=fth[nde]; 61 } 62 Splay(mem); 63 } 64 void Turnroot(int nde) 65 { 66 Access(nde),rev[nde]^=1; 67 } 68 int Getroot(int nde) 69 { 70 Access(nde); 71 while(son[nde][0]) 72 nde=son[nde][0]; 73 return nde; 74 } 75 void Split(int x,int y) 76 { 77 Turnroot(x),Access(y); 78 } 79 void Link(int x,int y) 80 { 81 Turnroot(x); 82 if(Getroot(y)!=x) 83 sizz[y]+=siz[x],fth[x]=y,Pushup(y); 84 } 85 int Change(int nde) 86 { 87 int sum1=0,sum2=0,ret=inf,oe=siz[nde]%2,haf=siz[nde]/2; 88 while(nde) 89 { 90 Release(nde); 91 int lson=son[nde][0],rson=son[nde][1]; 92 int nsm1=sum1+siz[lson],nsm2=sum2+siz[rson]; 93 if(nsm1<=haf&&nsm2<=haf) 94 { 95 if(oe) {ret=nde; break;} 96 else ret=min(ret,nde); 97 } 98 if(nsm1<=nsm2) sum1+=siz[lson]+sizz[nde]+1,nde=rson; 99 else sum2+=siz[rson]+sizz[nde]+1,nde=lson; 100 } 101 Splay(ret); 102 return ret; 103 } 104 void Linka(int x,int y) 105 { 106 int fx=Finda(x),fy=Finda(y); 107 Link(x,y),Split(fx,fy); int newc=Change(fy); 108 aset[fx]=aset[fy]=aset[newc]=newc,xrr^=fx^fy^newc; 109 } 110 int main() 111 { 112 scanf("%d%d",&n,&m); 113 for(int i=1;i<=n;i++) 114 xrr^=i,aset[i]=i; 115 while(m--) 116 { 117 scanf("%s",op); 118 if(op[0]=='X') 119 printf("%d\n",xrr); 120 else if(op[0]=='A') 121 scanf("%d%d",&t1,&t2),Linka(t1,t2); 122 else 123 { 124 scanf("%d",&t1); 125 printf("%d\n",Finda(t1)); 126 } 127 } 128 return 0; 129 }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号