洛谷P1073 最优贸易

传送门

Solution:

有一种显然的做法——缩点之后在DAG上dp。
对于一个强连通分量，假设在它当中的某个结点买入，另外一个结点卖出，那么对于该强连通分量内能获得的最大收益是$\max \{a[u]\}-\min \{a[u]\}$ ($u$为结点编号)
那么可以缩点，缩点之后变成DAG，想到可以在DAG上dp？设f[u]表示从$1$号点到$u$号点所经历的点中的水晶球价格的最小值，然后对于每个点用该点价格减去最小值，并与答案$ans$取个最大值。发现可行，因为没有后效性。

坑点：
题目要求从$1$号点到$N$号点，所以拓扑排序初始入队的结点只能为$1$号点。还需要dfs一遍判断某个点能否到达$N$号点。注意这里，调了9h的问题：

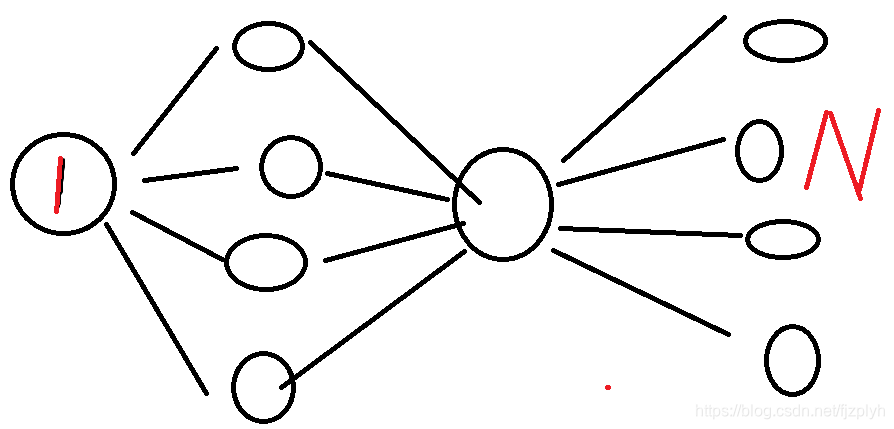
比如上面这张图片。从$1$号点开始遍历，第二列的每一个点将遍历到第四列的每一个点。那么假设第二列有$49999$个点，第四列有$49999$个点，则遍历的点大致有$50000^2$个。会超时。

解决办法是建反图从$N$号点开始遍历，建立vis数组判断一个点是否有遍历过。如果遍历过就不必再往下遍历——接下来的点肯定被遍历过了，肯定都能从$N$号点到达。

（图片忘记画方向了，脑补一下qwq）

code:

#include <iostream>
//#include <windows.h>
#include <cstdio>
#include <queue>
using namespace std;

const int MAXN = 1000007;
const int INF = 99999999;
int N, M, totN;
int val[MAXN];
struct Edge {
	int u, v, nxt;
	Edge (int u = 0, int v = 0, int nxt = 0) : u(u), v(v), nxt(nxt) {}
}newe[MAXN], befe[MAXN], oppe[MAXN];
// new新图，bef最开始的图，opp为新图的反图。
int newfir[MAXN], beffir[MAXN], oppfir[MAXN], newtote, beftote, opptote, newinp[MAXN];
int dfn[MAXN], ti, sta[MAXN], to, low[MAXN], book[MAXN], Amin[MAXN], Amax[MAXN];
int f[MAXN]; 
queue <int> Q;
int ans = 0;
bool is_arr[MAXN];
int vis[MAXN];

void befaddedge(int x, int y) {
	befe[++beftote] = Edge(x, y, beffir[x]);
	beffir[x] = beftote;
}
void newaddedge(int x, int y) {
	newe[++newtote] = Edge(x, y, newfir[x]);
	newfir[x] = newtote;
	newinp[y]++;
}
void oppaddedge(int x, int y) {
	oppe[++opptote] = Edge(x, y, oppfir[x]);
	oppfir[x] = opptote;
}
void tarjan(int x) {
	dfn[x] = low[x] = ++ti;
	sta[++to] = x;
	for(int i = beffir[x]; i; i = befe[i].nxt) {
		int y = befe[i].v;
		if(!dfn[y]) {
			tarjan(y);
			low[x] = min(low[x], low[y]);
		} else if(!book[y])
			low[x] = min(low[x], dfn[y]);
	}
	if(dfn[x] == low[x]) {
		book[x] = ++totN;
		Amax[totN] = Amin[totN] = val[x];
		while(sta[to] != x) {
			int h = sta[to];
			book[h] = totN;
			Amax[totN] = max(Amax[totN], val[h]);
			Amin[totN] = min(Amin[totN], val[h]);
//			ans = max(ans, Amax[totN] - Amin[totN]);
			--to;
		}
		--to;
	}
}
void Cre() {
	for(int i = 1; i <= N; i++)
		for(int j = beffir[i]; j; j = befe[j].nxt) {
			int x = befe[j].u, y = befe[j].v;
			if(book[x] != book[y]) newaddedge(book[x], book[y]), oppaddedge(book[y], book[x]);
		}
}
void dfs(int x) {
	is_arr[x] = true;
	for(int i = oppfir[x]; i; i = oppe[i].nxt) {
		int y = oppe[i].v;
		if(is_arr[y]) continue;
		dfs(y);
	}
}
void toposort() {
	for(int i = 1; i <= totN; i++) f[i] = INF;
//	for(int i = 1; i <= totN; i++) if(!newinp[i]) Q.push(i), f[i] = Amin[i], ans = max(ans, Amax[i] - Amin[i]);
	Q.push(book[1]), f[book[1]] = Amin[book[1]], ans = max(ans, Amax[book[1]] - Amin[book[1]]);
//	for(int i = 1; i <= totN; i++) if(!newinp[i]) printf("%d ", i);
	if(book[N] == book[1]) return;
	
	while(!Q.empty()) {
		int h = Q.front(); Q.pop();
		for(int i = newfir[h]; i; i = newe[i].nxt) {
			int y = newe[i].v;
			f[y] = min(f[h], Amin[y]);
			if(is_arr[y])
				ans = max(ans, Amax[y] - f[y]);
			newinp[y]--;
			if(!newinp[y] && book[N] != h) Q.push(y);
		}
	}
}
int main() {
	#ifdef test
		freopen("test.txt", "r", stdin);
	#endif
	cin >> N >> M;
	int x, y, id;
	for(int i = 1; i <= N; i++) scanf("%d", &val[i]);
	for(int i = 1; i <= M; i++) {
		scanf("%d %d %d", &x, &y, &id);
		befaddedge(x, y); 
		if(id == 2)
			befaddedge(y, x);
	}
	
	for(int i = 1; i <= N; i++)
		if(!dfn[i])
			tarjan(i);
	Cre();
	dfs(book[N]);
	toposort();
	
	cout << ans;
	return 0;
}