小h枕着二向箔睡觉(csp)

小h枕着二向箔睡觉(csp)

题目背景

这次并不是 \(\texttt{ycx}\) 来写背景，而是 \(\texttt{zkx}\) 来写背景。

这就是 \(\texttt{zkx}\) 写的关于 \(\texttt{ycx}\) 和 \(\texttt{zkx}\) 写背景一事的背景。

另：本题的题目名称的 \(\texttt{csp}\) 指的是 \({\color{red}{\texttt C}}\texttt{ongruence}\ {\color{red}{\texttt S}}\texttt{hortest}\ {\color{red}{\texttt P}}\texttt{ath}\)（同余最短路）的缩写。

题目描述

第一分钟，\(\texttt{hkh}\) 说：“要符合题目名称。”
于是小h拥有了一个二向箔。

第二分钟，\(\texttt{ys}\) 说：“要在二向箔上放一张图。”
于是现在有了两个点与一条连接这两个点的边。

第三分钟，\(\texttt{wcr}\) 说：“要给这条边加上权值。”
于是这唯一一条边的权值为 \(0\)。

第四分钟，\(\texttt{zjj}\) 说：“要让这张图有趣起来。”
于是又加了一条路径。

第五分钟，\(\texttt{ycx}\) 说：“要把这道题变得难一点。”
于是定义 \(u,v\) 两点的距离为 \(d_{u,v}=f(p-w_{u,v})\times g(w_{u,v})\)，其中 \(p\) 为给定的质数，\(w_{u,v}\) 指边 \(u-v\) 的权值，且 \(f(x)=p^x,g(x)=A_{px}^{(p-1)x}\)。

第六分钟，\(\texttt{cyh}\) 说：“毛。”
于是便设原来的距离（即 \(1-2\)）为 \(d_1\)，后来的距离（即 \(1-3-4-5-2\)）为 \(d_2\)，因为要有最短路，所以有了 \(d_2\over d_1\)，因为还要有同余，所以设 \({d_2\over d_1}\equiv d\pmod p\)

第七分钟，\(\texttt{zkx}\) 说：“要有一个良心出题人。”
于是他给定了 \(p,d(0\le d\le p-1)\)，并且规定后来添加的权值（即数列 \(k\)）必须在 \([1,p]\) 中，且互不相同，另外后来添加的边权数 \(n\le\lfloor{p\over2}\rfloor\)。

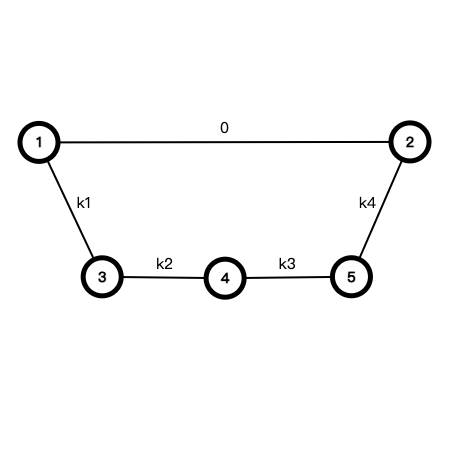
（图中的数据代表该边的权值）

你现在的任务即构造一组后来添加的边权（即数列 \(k\)），使得以上要求满足。

输入格式

一行两个整数 \(d,p\)。

输出格式

第一行一个整数 \(n\)，表示新增的边权数，即序列 \(k\) 的个数。

第二行为构造的序列 \(k\)，第 \(i\) 个数表示 \(k_i\)。

样例

样例输入 1

0 3

样例输出 1

0

样例输入 2

1 3

样例输出 2

1
2

样例输入 3

3 5

样例输出 3

2
1 3

样例输入 4

17 19

样例输出 4

8
1 4 7 9 10 13 16 19

数据范围与提示

样例解释1

\(d_1=f(3-0)\times g(0)=3^3\times A_{0}^{0}=27\)
不存在第二条路径，则 \(d_2=0\)
\({d_2\over d_1}={0\over 27}=0\equiv0\pmod 3\)

样例解释2

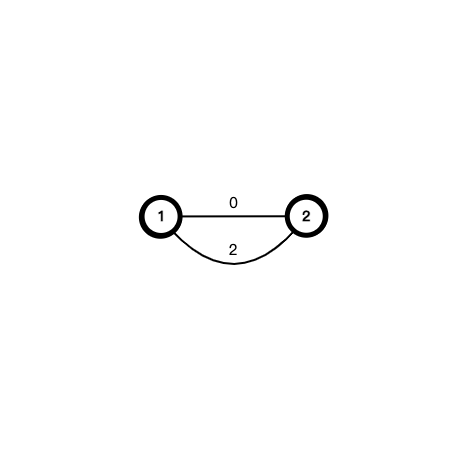
\(d_1=f(3-0)\times g(0)=3^3\times A_{0}^{0}=27\)
\(d_2=f(3-2)\times g(2)=3^1\times A_{6}^{4}=1080\)
\({d_2\over d_1}={1080\over 27}=40\equiv1\pmod 3\)

样例解释3

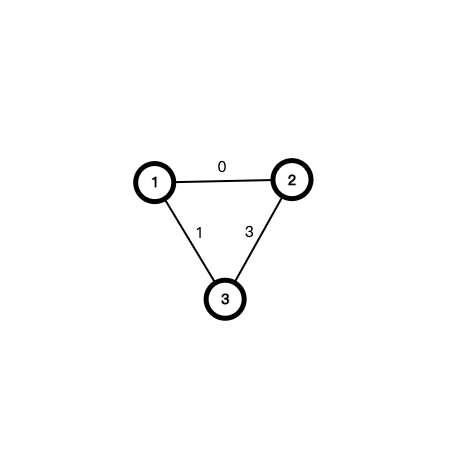
\(d_1=f(5-0)\times g(0)=5^5\times A_{0}^{0}=3125\)
\(d_2=f(5-1)\times g(1)+f(5-3)\times g(3)=5^4\times A_{5}^{4}+5^2\times A_{15}^{12}=75000+5448643200000=5448643275000\)
\({d_2\over d_1}={5448643275000\over 3125}=1743565848\equiv3\pmod 5\)

对于 \(100\%\) 的数据，\(2\le p\le 10^6+3,0\le d\le p-1\)，保证 \(p\) 为质数。

一句话题意

给定 \(d,p\)，保证 \(p\) 为质数，\(0\le d\le p-1\)。

你需要构造一个序列 \(k_i(1\le i\le n)\)，满足：

1. \(1\le n\le \lfloor\frac{p}{2}\rfloor\)

2. 对于任意的 \(i(1\le i\le n)\)，满足 \(1\le k_i\le p\)

3. 对于任意的 \(i,j(1\le i<j\le n)\)，满足 \(k_i\ne k_j\)

4. 满足 \({\displaystyle\sum_{i=1}^np^{p-k_i}\times A_{pk_i}^{(p-1)k_i}\over p^p}\equiv d\pmod p\)

solution

题解

\( \begin{align} \nonumber {\displaystyle\sum_{i=1}^np^{p-k_i}\times A_{pk_i}^{(p-1)k_i}\over p^p}&=\displaystyle\sum_{i=1}^n{p^{p-k_i}\times A_{pk_i}^{(p-1)k_i}\over p^p}\\ \nonumber &=\displaystyle\sum_{i=1}^n{A_{pk_i}^{(p-1)k_i}\over p^{k_i}}\\ \nonumber &=\displaystyle\sum_{i=1}^n{(pk_i)!\over k_i!p^{k_i}}\\ \nonumber &=\displaystyle\sum_{i=1}^n\displaystyle\prod_{i=1,p\nmid i}^{pk_i}i\\ \nonumber &\equiv \displaystyle\sum_{i=1}^n(p-1)!^{k_i}\pmod p \end{align} \)

由于 \(p\) 为质数，因此有威尔逊定理 \((p-1)!\equiv -1\pmod p\)

因此 \({\displaystyle\sum_{i=1}^np^{p-k_i}\times A_{pk_i}^{(p-1)k_i}\over p^p}\equiv \displaystyle\sum_{i=1}^n(-1)^{k_i}\pmod p\)

当 \(d\le\lfloor{p\over2}\rfloor\) 时，可以由 \(d\) 个偶数解决问题。

否则，当 \(d>\lfloor{p\over2}\rfloor\) 时，\(p-d\le\lfloor{p\over2}\rfloor\)，可以由 \(p-d\) 个奇数解决问题。

std

#include<iostream>
#include<cstdio>
using namespace std;
int d,p,f,n;
int main()
{
    scanf("%d%d",&d,&p);
    if(d<=p/2) f=0,n=d;
    else f=-1,n=p-d;
    printf("%d\n",n);
    for(int i=1;i<=n;i++) printf("%d ",2*i+f);
    printf("\n");
    return 0;
}

后话

吐槽

思维简单，代码好写，没有毒瘤的小清新题目。

总结

\(100\times 1+0\times 2=100\)

平均得分：\(33.33\)

大家看到数学式子都不想做了（确信）