noip模拟13 工业题 卡常题 玄学题
有史以来想法最接近正解的一次?
首次有两道数学的比赛,而且都想到了正解,但都写挂了。
两天挂三道数学的奇迹(
\(\color{white}{(5)}12\)的\(\mathrm{rank}\dots\)
都不重要(bushi
考场上顺序开题。
\(\mathrm{A.}\mathbb{工业题}\):数学

\(\mathrm{B.}\mathbb{卡常题}\):图论
\(\mathrm{C.}\mathbb{玄学题}\):还是TMD数学

都看完一遍后觉得这场比赛能上 \(200\)。(当时都不知道哪来的自信)
前 \(\mathrm{1h}\) 几乎都在推 \(\mathrm{A}\) 的式子,从最后一个挨个往前找,最终还是通过比较得当的方法找规律,推出了式子,连写带调大约又用了 \(\mathrm{1h}\),测了个大样例,觉得没什么问题就交了。
(隔壁dalao因为本地的玄学错误,调了 \(\mathrm{30min}\))
后面的时间几乎都在推 \(\mathrm{C}\),并且在距离比赛结束还有 \(\mathrm{1h}\) 的时候成功推出了式子。并且和正解一模一样。

在最后的几分钟里给 \(\mathrm{B}\) 写了个 \(\mathrm{rand}\),虽然 \(\mathrm{CE}\) 了,不过也没什么影响。
估分:\(100+0+100=200\)
实际:\(30+0+80=110\)

还是说正解吧(
A.工业题
一点都不工业。
这题考场上用很sb的方法一个一个往前推,推出来的式子竟然还没有完全错。
推对了一半的式子,得了不到一半的分。
正解
直接考虑求第 \(0\) 行和第 \(0\) 列的系数,然后对应相乘再相加即可。
设 \(d_{i,j}\) 表示第 \(i\) 行第 \(j\) 列格子的系数,显然有:
-
对于任意一个\(i\in[1,n]\),都有\(d_{i,0}=d_{i,1}\)
-
对于任意一个\(i\in[1,m]\),都有\(d_{0,i}=d_{1,i}\)
由这两个性质,就可以知道:
-
对于任意一个 \(i\in[1,n]\),\(d_{i,0}=(i,1)\) 走到 \((n,m)\) 的方案数 \(\times a^{\mathbb{向右走的步数}}\times b^{\mathbb{向下走的步数}}\)
-
对于任意一个 \(i\in[1,m]\),\(d_{0,i}=(1,i)\) 走到 \((n,m)\) 的方案数 \(\times a^{\mathbb{向右走的步数}}\times b^{\mathbb{向下走的步数}}\)
组合数与幂可以递推求解。
因此我们就能得到下面这张表。
\( \begin{array}{|c|c|} \hline &0&1&2&\cdots&j&\cdots&m\\\hline 0&0&C_{n+m-2}^{n-1}a^{m-1}b^n&C_{n+m-3}^{n-1}a^{m-2}b^n&\cdots&C_{n+m-j-1}^{n-1}a^{m-j}b^n&\cdots&C_{n-1}^{n-1}a^0b^n\\\hline 1&C_{n+m-2}^{m-1}a^mb^{n-1}&0&0&\cdots&0&\cdots&0\\\hline 2&C_{n+m-3}^{m-1}a^mb^{n-2}&0&0&\cdots&0&\cdots&0\\\hline \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\\hline i&C_{n+m-i-1}^{m-1}a^mb^{n-i}&0&0&\cdots&0&\cdots&0\\\hline \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\ddots&\vdots\\\hline n&C_{m-1}^{m-1}a^mb^0&0&0&\cdots&0&\cdots&0\\\hline \end{array} \)
code
#include<iostream>
#include<cstdio>
using namespace std;
const int N=3e5+5,mod=998244353;
int n,m;
long long a,b;
long long r[N],c[N];
long long mul=1,fac[N],invfac,inv[N];
long long power(long long b,long long p)
{
long long ans=1;
while(p)
{
if(p&1) ans=ans*b%mod;
p>>=1;
b=b*b%mod;
}
return ans;
}
long long ans;
int main()
{
scanf("%d%d%lld%lld",&n,&m,&a,&b);
a%=mod,b%=mod;
for(int i=1;i<=n;i++) scanf("%lld",&c[i]),c[i]%=mod;
for(int i=1;i<=m;i++) scanf("%lld",&r[i]),r[i]%=mod;
for(int i=1;i<=max(n,m)-1;i++) inv[i]=power(i,mod-2);
fac[0]=1;
for(int i=1;i<=max(n,m)-1;i++) fac[i]=fac[i-1]*i%mod;
mul=fac[m-1];
invfac=power(mul,mod-2);
long long powa=power(a,m),powb=power(b,n);
long long aa=1,bb=1;
for(int i=1;i<=n;i++)
{
ans=(ans+mul*c[n-i+1]%mod*invfac%mod*powa%mod*bb%mod)%mod;
mul=mul*inv[i]%mod*(m+i-1)%mod;
bb=b*bb%mod;
}
mul=fac[n-1];
invfac=power(mul,mod-2);
for(int i=1;i<=m;i++)
{
ans=(ans+mul*r[m-i+1]%mod*invfac%mod*powb%mod*aa%mod)%mod;
mul=mul*inv[i]%mod*(n+i-1)%mod;
aa=a*aa%mod;
}
printf("%lld\n",ans);
return 0;
}
B.卡常题
一点都不卡常
这题考场上看都没看,写了个 \(\mathrm{rand}\) 还 \(\mathrm{CE}\) 惹。
正解
看到 \(Y\) 方点的度数为 \(2\),因此我们可以很自然的想到把 \(Y\) 方点直接去掉,看作是一条连接两个 \(X\) 方点的边。
由于它保证连通,所以这道题就变成了一棵 \(n\) 个点 \(n\) 条边的基环数的最小点覆盖问题。
用并查集找到环,随便破一条边,并记录这条边的两个点,强制这两个点覆盖与他相连的那条边,从这两个点开始做类似这道题树形 \(\mathrm{dp}\)
答案即为 \(\min(f_{\mathrm{root1},1},f_{\mathrm{root2},1})\)
code
#include<iostream>
#include<cstring>
using namespace std;
int n,a,b;
const int N=1e6+5;
int head[N],sum[N],fa[N];
int f[N][2];
int cnt,ans;
int root1,root2;
struct Node
{
int to,nxt;
}e[N*2];
void add(int u,int v)
{
e[++cnt].to=v;
e[cnt].nxt=head[u];
head[u]=cnt;
}
int get(int x)
{
if(x==fa[x]) return x;
return fa[x]=get(fa[x]);
}
void merge(int x,int y)
{
fa[get(x)]=get(y);
}
void dp(int u,int fa)
{
f[u][0]=0;
int sumn=0;
for(int i=head[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(v==fa) continue;
dp(v,u);
sumn+=min(f[v][0],f[v][1]);
f[u][0]+=f[v][1];
}
f[u][1]=sum[u]+sumn;
}
int main()
{
cin>>n>>a>>b;
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=n;i++)
{
int x,y;
cin>>x>>y;
sum[x]+=a;
sum[y]+=b;
if(get(x)==get(y))
{
root1=x;
root2=y;
continue;
}
merge(x,y);
add(x,y);
add(y,x);
}
dp(root1,0);
ans=f[root1][1];
memset(f,0,sizeof(f));
dp(root2,0);
ans=min(ans,f[root2][1]);
cout<<ans<<endl;
return 0;
}
C.玄学题
这题确实很玄学
这题用了 \(\mathrm{1h}\) 来推式子,最后推出来了,但是因为多开了几个 \(\mathrm{long\ long}\) 而导致 \(100\) 挂成 \(80\)(悲)
正解

因此我们只需要预处理出 \(\mathrm{min}_i\) 即可。
正解应该是线性求,但我写的多了一个 \(\log\),因此会被卡掉 \(5\) 分,所以多交了几次。
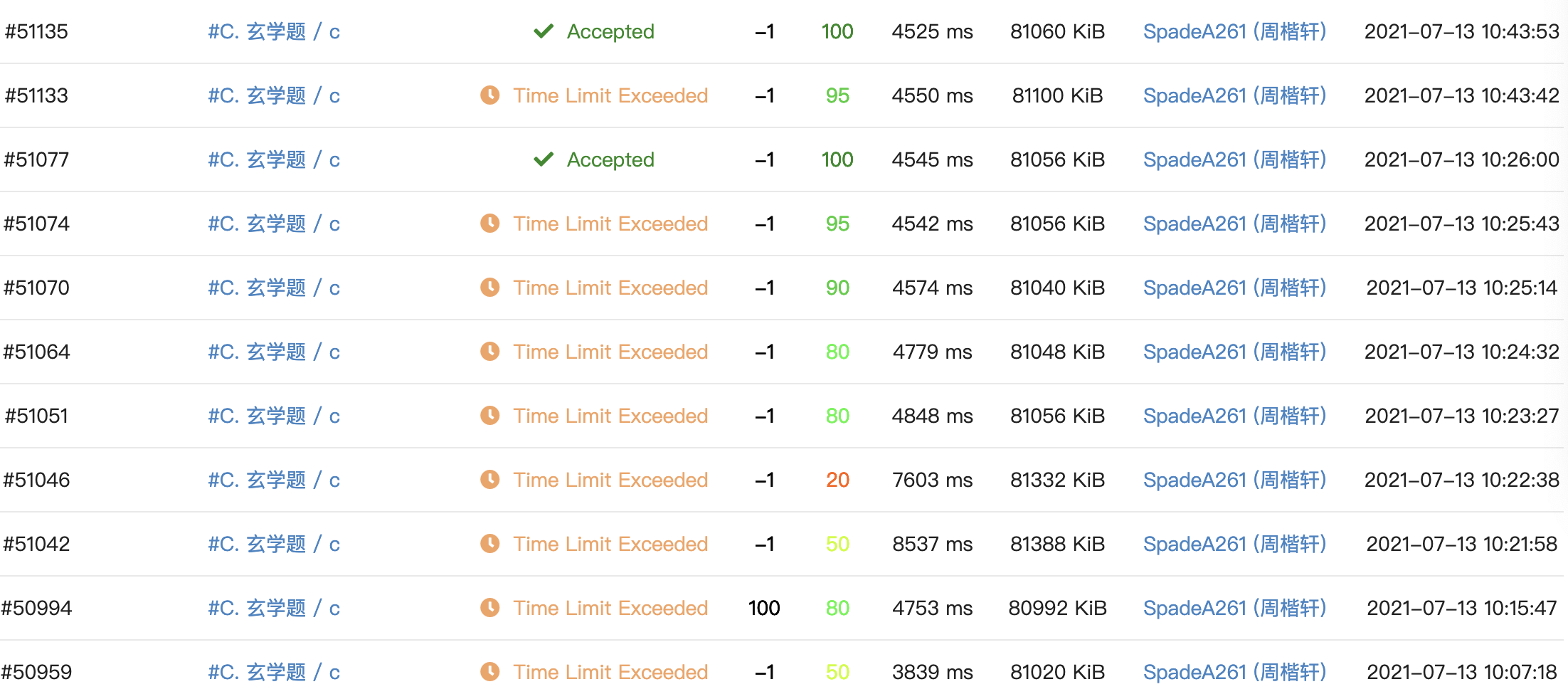
《论如何暴力艹标算》
想要看线性求的可以移步dalao的博客
code
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int N=1e7+5;
int n,p;
long long m;
int mn[N],ans;
int v[N],prime[N];
int gcd(int a,int b)
{
if(b==0) return a;
return gcd(b,a%b);
}
void primes(int n)
{
p=0;
mn[1]=1;
for(int i=2;i<=n;i++)
{
if(v[i]==0)
{
v[i]=i;
prime[++p]=i;
mn[i]=i;
}
for(int j=1;j<=p;j++)
{
if(prime[j]>v[i]||prime[j]>n/i) break;
v[i*prime[j]]=prime[j];
int d=gcd(mn[i],prime[j]);
mn[i*prime[j]]=mn[i]/d*prime[j]/d;
}
}
}
int main()
{
scanf("%d%lld",&n,&m);
primes(n);
for(int i=1;i<=n;i++)
{
int cnt=sqrt(m/mn[i]);
if(cnt&1) ans--;
else ans++;
}
printf("%d\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号