300IQ contest3 A Airplane Cliques&校内训练树上开花

题面

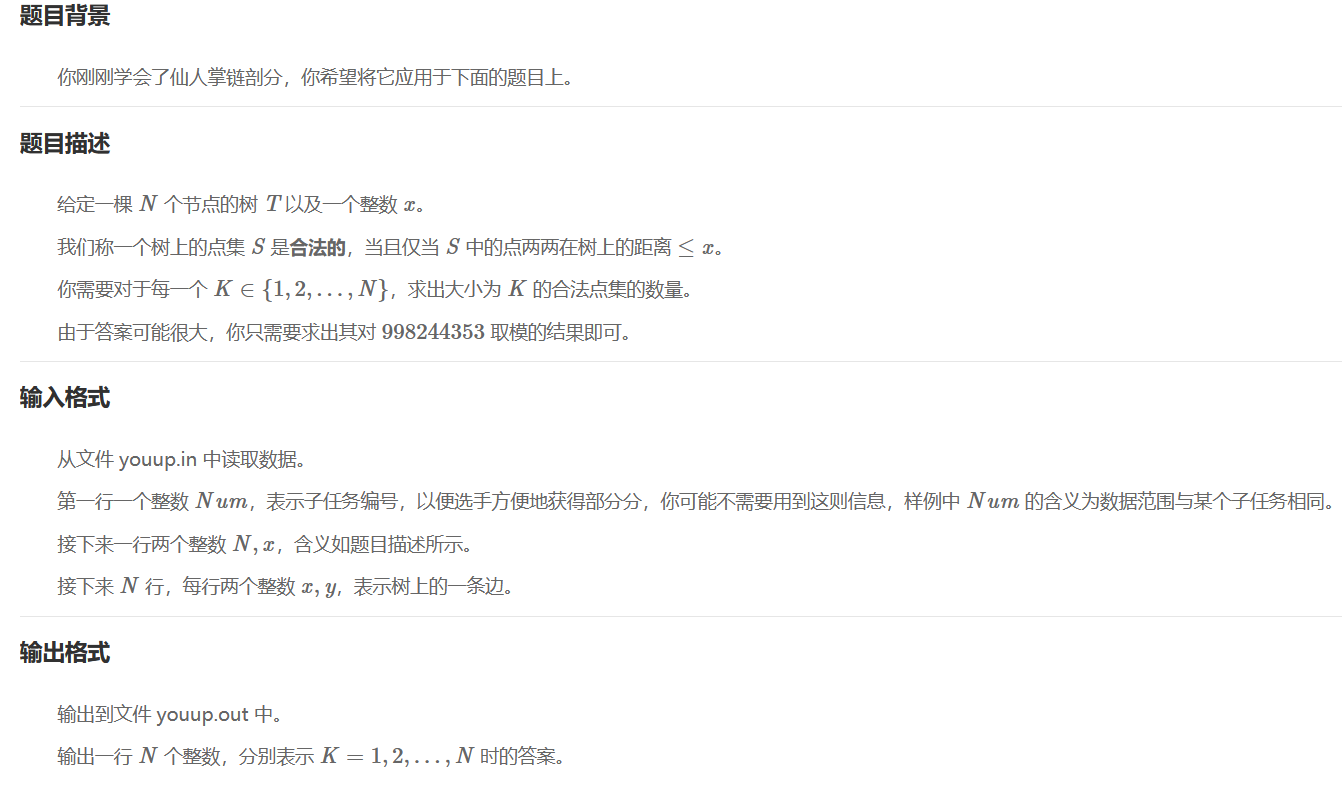
solution：
考虑在原树的每一条边处插入一个点，使得x变为偶数。
引理：集合 \(S\) 是合法的当且仅当存在点 \(p\) ， 满足 \(p\) 到 \(S\) 中各点距离均 \(\leqslant\) \(\frac {x} {2}\)
引理：：充分性显然。必要性的证明则是，\(p\) 为集合直径中点时合法。
并且，我们可以发现，对于一个合发几盒 \(S\) ，满足条件的 \(p\) 构成了树上的一个联通块。因此可以考虑使用“点数减边数”的方式对联通块进行容斥，计算答案。
我们希望对于树上的每一个点计算出 \(v_i\) 表示与其距离在 \(\frac {x} {2}\) 之内的点的个数。与此同时求出 \(e_i\) 表示两个端点距离均在 \(\frac {x} {2}\) 以内的点的个数。
则答案为
\(Ans_i = \Sigma_{j\in V} C_{v_j}^i\) - \(\Sigma_{j\in E} C_{e_j}^i\)
代码因为个人能力限制，暂时写不出来（