CF506E

CF506E

• 给定一个小写字符串 \(s\) 和一个正整数 \(n\)。
• 要求在 \(s\) 中插入恰好 \(n\) 个小写字符使其回文的方案数。
• \(|s| \le 200,n \le 10^9\)，答案对 \(10^4 + 7\) 取模。

Solution

我们先来考虑怎么样的一个字符串是可以被构成的。

• 其长度为 \(n+|s|\)。
• 其回文。
• 其存在一个子序列为 \(s\)

先假设 \(n+|s|\) 为偶数。

我们考虑条件 3 是否存在其他描述，我们发现由于回文，所以我们计数的时候只能对于其中的一半计数。

同样由于回文，我们发现一个回文串合法，当且仅当其从前匹配 \(s\) 可以到达 \(t_1\)，从后匹配 \(s\) 可以到达 \(t_2\)，如果 \(t_2+t_1>|s|\) 那么就合法。

然后可以设计状态来进行 dp 了，大概是 \(f_{i,j,k}\) 表示到了位置 \(i\) 从开头匹配了 \(j\) 位，结尾匹配了 \(k\) 位的方案数。

于是状态可以更新为 \(f_{i,j,k}\) 表示当前考虑到 \(T\) 的第 \(i\) 个字符， \(s\) 还剩余区间 \([j,k]\) 进行匹配的方案数。

转移根据 \(s_j\) 和 \(s_k\) 是否相等进行分类讨论，对于 \(j>k\) 的情况转移到 \(j>k\) （或者说 end 的状态）

暴力优化，复杂度 \(\mathcal O(|s|^6\log n)\)

我们发现事实上我们的转移是一个在有限自动机上匹配的过程：

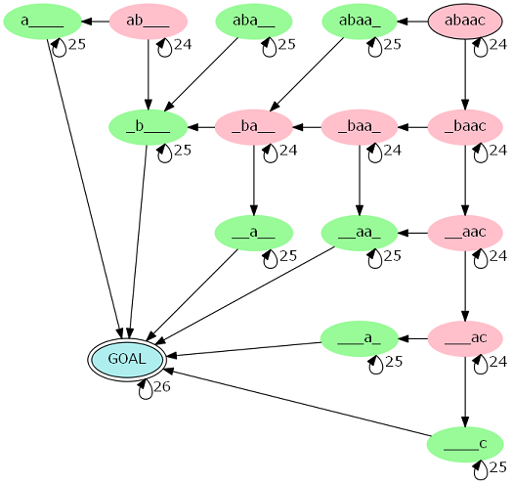
上图是对 abaac 建立的自动机的模型。

其中，我们令满足 \(s_j=s_k\) 的点为绿色点，转移至自己的系数为 \(25\)，满足 \(s_j\ne s_k\) 的点为红色点，转移至自己的系数为 \(24\)

这样我们可以基于一个这样的考虑，我们可以考虑先确定一条路线，再考虑有多少种方案经过了此路线：

假设这条路线经过了 \(m\) 个红色点，那么不难发现他一定经过了 \(\lceil\frac{|s|-m}{2}\rceil\) 个绿色点。

我们发现非自环的边只会走一次，这样我们可以考虑给每个点确定其自环的使用次数。

这样我们等价于分配一组系数 \(c_1,c_2...c_k,\rm{goal}\)，然后答案即为 \(24^{\sum c_l}\times 25^{\sum c_r}\times 26^{\rm{goal}}\)

于是不难看出每种经过红色点数相同的路径对答案的贡献都是相同的。

考虑确定了红色点和绿色点的数量 \(a\) 和 \(b\) 之后我们如何计算答案，不难发现我们本质上想要计算的是：

\[\bigg(\sum 24^ix^i\bigg)^a\times \bigg(\sum 25^ix^i\bigg)^b\times \bigg(\sum 26^i x^i\bigg)[x^n] \]

由于 \(n\) 非常大，我们考虑通过 dp 来计算答案，形如 \(f_{i,j}\) 表示处理到第 \(i\) 个多项式，\(x^{j}\) 前系数，转移形如 \(f_{i,j}=f_{i-1,j}+(24/25/26)f_{i-1,j-1}\)

当然可以矩阵快速幂加速，复杂度为 \(\mathcal O(|s|^4\log n)\)

事实上也可以当作是自动机上匹配的过程。

观察到 \(a\uparrow,b\downarrow\)，所以我们可以构建一个这样的自动机：

然后总点数就只有 \(\frac{3}{2}s\)，跑 \(\mathcal O(|s|^3\log n)\) 的 Dp 就 win 了。

然后如果 \(n+|s|\) 为奇数，我们就计算 \(n+|s|+1\) 情况下的矩阵，然后减去非法的情况即可，这些非法的情况即最终限制长度为 \(2\) 的绿点无法转移即可。（我们删去终点到终点的自环即可）

复杂度 \(\mathcal O(|s|^3\log n)\)

\(Code:\)

#include<bits/stdc++.h>
using namespace std ;
#define Next( i, x ) for( register int i = head[x]; i; i = e[i].next )
#define rep( i, s, t ) for( register int i = (s); i <= (t); ++ i )
#define drep( i, s, t ) for( register int i = (t); i >= (s); -- i )
#define re register
int gi() {
	char cc = getchar() ; int cn = 0, flus = 1 ;
	while( cc < '0' || cc > '9' ) {  if( cc == '-' ) flus = - flus ; cc = getchar() ; }
	while( cc >= '0' && cc <= '9' )  cn = cn * 10 + cc - '0', cc = getchar() ;
	return cn * flus ;
}
const int P = 1e4 + 7 ; 
const int N = 200 + 5 ;
const int M = 300 + 5 ;  
int n, m, lim, fl, Id[N][N], dp[N][N][N] ; 
char s[N] ; 
struct Mat {
	int a[M][M] ; 
	void init() { rep( i, 1, lim ) rep( j, 1, lim ) a[i][j] = 0 ; }
	void init2() { init() ; rep( i, 1, lim ) a[i][i] = 1 ; }
} A, f ; 
Mat operator * (Mat x, Mat y) {
	Mat ans ; ans.init() ;
	rep( k, 1, lim ) rep( i, 1, lim ) rep( j, 1, lim ) 
		ans.a[i][j] = (ans.a[i][j] + x.a[i][k] * y.a[k][j]) % P ; 
	return ans ; 
}
Mat fpow(Mat x, int k) {
	Mat ans, base = x ; ans.init2() ; 
	while(k) {
		if(k & 1) ans = ans * base ;
		base = base * base, k >>= 1 ; 
	} return ans ; 
}
void Dfs(int l, int r) {
	if( l > r ) return dp[l][r][0] = 1, void() ; 
	if( Id[l][r] ) return ; Id[l][r] = 1 ; 
	if(s[l] == s[r]) {
		Dfs(l + 1, r - 1) ; 
		rep(i, 0, m) dp[l][r][i] = dp[l + 1][r - 1][i] ; 
	}
	else {
		Dfs(l + 1, r), Dfs(l, r - 1) ; 
		rep(i, 1, m) dp[l][r][i] = (dp[l + 1][r][i - 1] + dp[l][r - 1][i - 1]) % P ; 
	}
}
void Dfs2(int l, int r) {
	if( Id[l][r] > 1 ) return ; Id[l][r] = 2 ; 
	rep( i, 0, m ) dp[l][r][i] = 0 ; 
	if( l > r ) return dp[l][r][0] = 1, void() ; 
	if(s[l] == s[r]) {
		if( r == l ) return ; 
		Dfs2(l + 1, r - 1) ; 
		rep(i, 0, m) dp[l][r][i] = dp[l + 1][r - 1][i] ; 
	} else {
		Dfs2(l + 1, r), Dfs2(l, r - 1) ; 
		rep(i, 1, m) dp[l][r][i] = (dp[l + 1][r][i - 1] + dp[l][r - 1][i - 1]) % P ; 
	}
}
signed main()
{
	scanf("%s", s + 1 ), m = strlen(s + 1) ;
	n = gi(), n += m ; if(n & 1) ++ n, fl = 1 ;
	Dfs(1, m) ; lim = m + ((m + 1) / 2) ; 
	rep( i, 1, m - 1 ) {
		f.a[i][i] = 24, f.a[i][i + 1] = (i != (m - 1)),
		f.a[i][lim - (m - i + 1) / 2] = dp[1][m][i] ; 
	} 
	for(re int i = m; i < lim; ++ i) 
		f.a[i][i + 1] = 1, f.a[i][i] = 25 ; 
	f.a[lim][lim] = 26, A = fpow(f, n / 2) ;
	int ans = 0 ; 
	if( m != 1 ) ans = A.a[1][lim] ;
	ans = (ans + A.a[m][lim] * dp[1][m][0] % P) % P ; 
	if( fl ) {
		memset( f.a, 0, sizeof(f.a) ), Dfs2(1, m) ; 
		rep( i, 1, m - 1 ) {
			f.a[i][i] = 24, f.a[i][i + 1] = (i != (m - 1)), 
			f.a[i][lim - (m - i + 1) / 2] = dp[1][m][i] ; 
		} 
		for(re int i = m; i < lim; ++ i) 
			f.a[i][i + 1] = 1, f.a[i][i] = 25 ; 
		A = fpow(f, n / 2) ;
		if(m != 1) ans = (ans - A.a[1][lim] + P) % P ;
		ans = (ans - A.a[m][lim] * dp[1][m][0] % P + P) % P ; 
	}
	cout << ans << endl ; 
	return 0 ; 
}