CF848D Shake It!
CF848D Shake It!
给定 \(n,m\),现在按照此规则生成无向图,初始我们有一张图 \(G\),仅包含两个节点 \(s,t\),以及连接 \(s\to t\) 的边。
每次你可以选择一条已经存在的边 \((u,v)\),然后将往图中加入节点 \(w\) 和边 \((u,w),(w,v)\),这样操作 \(n\) 次,我们将得到一张图 \(G'\)
定义 \(G'\) 合法,当且仅当 \(\min cut(s,t)=m\),即 \(s\to t\) 的最小割为 \(m\)
求本质不同的合法的图 \(G'\) 的数量,答案对 \(10^9+7\) 取模。
其中,两张图 \(G_1,G_2\) 不同,当且仅当不存在一种作用于点集的置换,使得边对应相同,同时 \(s,t\) 对应相同。
\(n,m\le 50\)
translated by EmptySoulist
Solution
方便起见,我们认为一次给 \((u,v)\) 加入 \(w\) 的操作为 "加点/添加节点" 操作,我们使用 \((u\to w\to v)\) 来描述此操作。
同时,不难通过观察发现加点有且仅有两种方向(Left and Right)。
请注意,此图上允许对一条边重复添加节点,这非常重要。
我们不难观察到这张图一定是平面图,平面图最小割等于对偶图最短路。
如果不考虑给一条边重复添加节点的情况,我们发现增加节点的过程在对偶图上非常类似于树的形态,考虑一棵树,儿子有 \(0,1\) 两种颜色( \(0\) 表示从左边加,\(1\) 表示右边加)每次增加节点的时候我们给其赋予一个颜色即可。
不难发现此时对偶图最短路即这棵树深度最小的儿子的深度。
接着我们再考虑,允许重复添加节点的情况,我们假设 \((u\to v)\) 的边被加入了两次 \((u\to w_1\to v,u\to w_2\to v)\),同时 \(u\to w_1\) 等边也被加入过点。
我们发现这张平面图上这些边的 内外 顺序是可以任意调控的,这间接使得我们想到,答案应该是只考虑 \(u\to w_1\to v\) 的边存在的情况和 \(u\to w_2\to v\) 存在的情况下答案的和。
通过简单的画图也可以说明这件事。下面将给出一个例子:

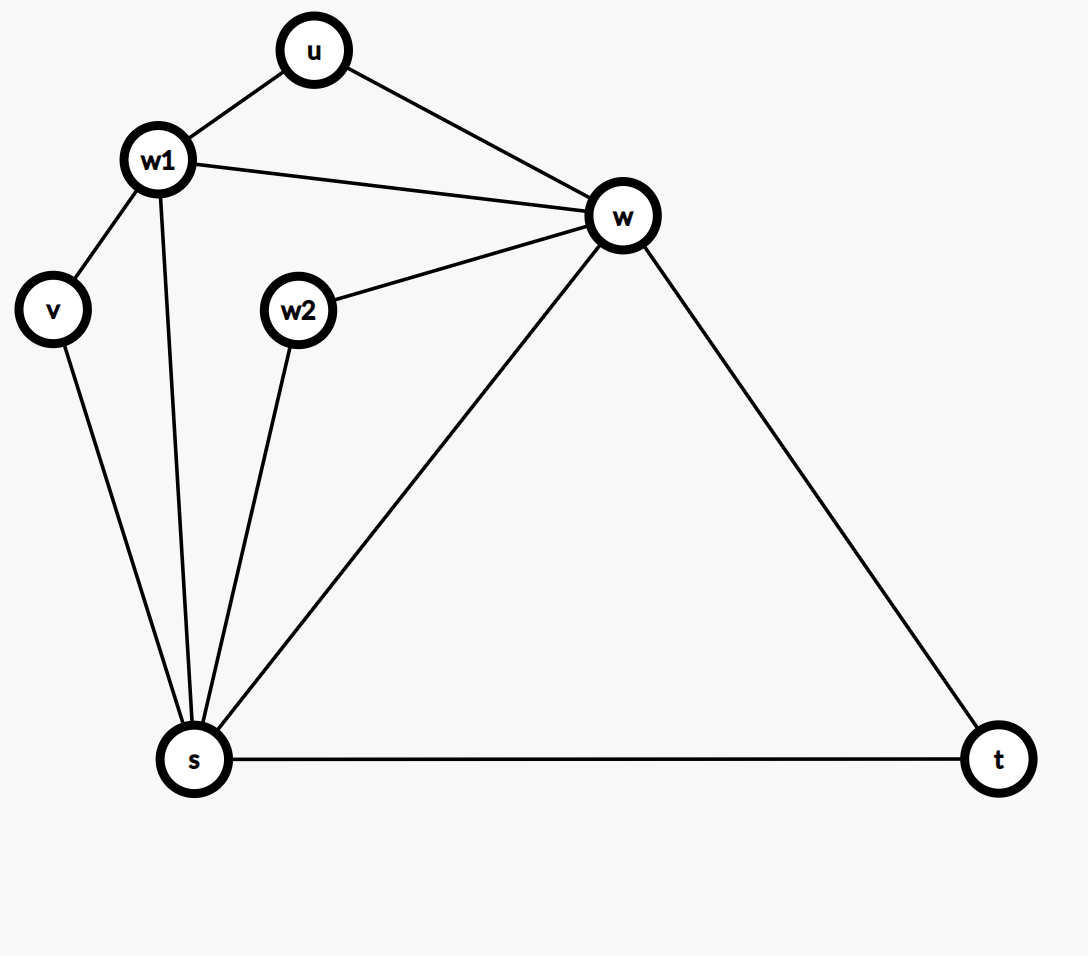
第二张图对应的对偶图形如如此:

(保留了 \(s\to t\) 的边方便观看)
其中 \(A\to G\) 的最短路即为答案。
进一步简化,两张图对应的对偶图分别为:
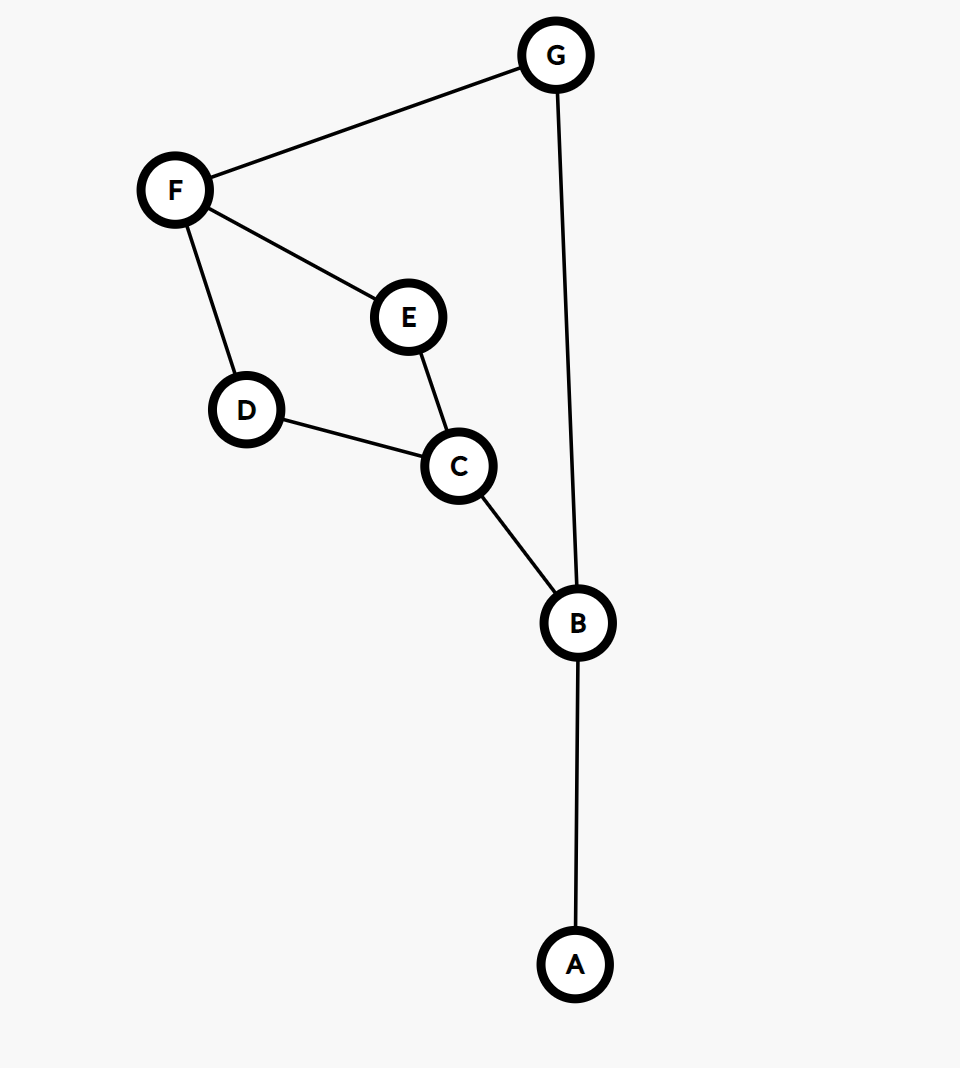
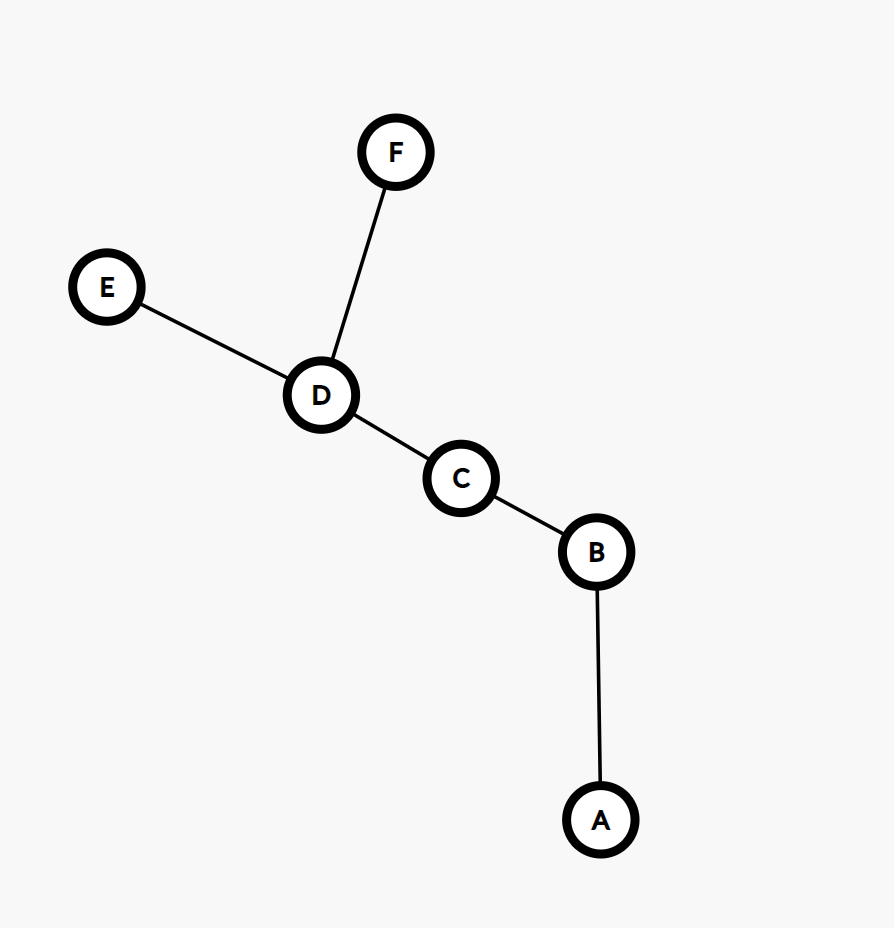
第二张图删去了与 \(G\) 的连边。
注意到这两张图本质上是相同的,也出于进一步的观察,我们不难发现我们可以对真实的对偶图进行一步简化,在初始建图中,假设某条边被操作了 \(k\) 次(且方向相同)我们可以类似于没有边被重复操作时的例子,直接建成树的形态,将这 \(k\) 条边同时挂在 \(u\to v\) 这条边对应的点之下,假设这些边的方向均为 Left,我们发现答案即为这些独立树的答案和!
证明的话画一下图就知道了(具体论证有点麻烦,我不太方便画图 TAT)。
假设 Left 为颜色 \(0\),Right 为颜色 \(1\),那么我们不难得到对一棵简化的树计算答案的方法:
由于初始根没有方向区分,所以我们只能将这张图建成森林,其贡献即为各棵子树根节点的 \(f\) 之和 \(+1\)
我们发现本质不同的图,等价于这样简化后的树不同。
那么考虑对树进行计数,我们设 \(g_{i,j}\) 表示 \(i\) 个节点的树,其根节点 \(f\) 值为 \(j\) 的树的方案数。
我们发现本质不同其实说明儿子任意交换对答案没有影响,那么这里类似于无排列规则的计数问题。比如两棵树形如 \(1,2,2\),那么 \(212,122,221\) 均被视为相同的排列。
于是我们对 left 和 right 分别进行转移,然后通过一次类似于卷积的形式合并答案即可。
其中,left 和 right 在转移的过程使用的数组相同,我们发现问题的核心点在于如何去重上了,我们使用 \(f\) 数组来表示我们需要的答案。
假设从小到大加入元素,此时 \(i\) 是我们最后加入的元素,对于 \(i,j\) 不同的元素,我们从小到大枚举 \(j\),这样我们保证了 \((i,j)\) 的对子是按照 \(i\) 为第一关键字,\(j\) 为第二关键字从小到大加入集合的。
对于 \((i,j)\) 相同的对子,我们发现问题等价于有 \(g_{i,j}\) 个数,每个数出现次数任意,如果所有数出现次数相同那么算同一种方案,求方案数。
假设 \(g_{i,j}\) 被使用了 \(k\) 次,那么不难发现贡献即 \(\binom{g_{i,j}+k-1}{k}\),即 \(\frac{1}{(1-x)^k}[x^{g_{i,j}}]\),是经典模型,这样的话我们需要枚举 \(k\)。
每次转移得到 \(f\) 之后,我们不难转移 \(g\)
\(g_{i,j}\leftarrow \sum_{u+v=i-1,\min(l,r)=j-1}f_{u,l}f_{v,r}\)
这样我们一边递推 \(g\),一遍递推 \(f\) 即可。
边界为 \(g_{1,1}=1\),同时不难发现我们需要的答案即为 \(f_{n,m-1}\)
复杂度为 \(\mathcal O(n^4\ln n)\)
枚举顺序上有一些坑,建议多想想后写。
\(Code:\)
#include<bits/stdc++.h>
using namespace std ;
#define rep( i, s, t ) for( register int i = (s); i <= (t); ++ i )
#define drep( i, s, t ) for( register int i = (t); i >= (s); -- i )
#define re register
#define int long long
int gi() {
char cc = getchar() ; int cn = 0, flus = 1 ;
while( cc < '0' || cc > '9' ) { if( cc == '-' ) flus = - flus ; cc = getchar() ; }
while( cc >= '0' && cc <= '9' ) cn = cn * 10 + cc - '0', cc = getchar() ;
return cn * flus ;
}
const int P = 1e9 + 7 ;
const int N = 50 + 5 ;
int n, m, g[N][N], f[N][N], fac[N], inv[N], D[N][N][N] ;
int fpow(int x, int k) {
int ans = 1, base = x ;
while(k) {
if(k & 1) ans = ans * base % P ;
base = base * base % P, k >>= 1 ;
} return ans ;
}
void inc(int &x, int y) {
((x += y) >= P) && (x -= P) ;
}
int C(int x, int y) {
int ans = 1 ;
rep( i, 1, y ) ans = ans * (x - i + 1) % P ;
return ans * inv[y] % P ;
}
signed main()
{
n = gi(), m = gi() ; fac[0] = inv[0] = 1 ;
rep( i, 1, n ) fac[i] = fac[i - 1] * i % P, inv[i] = fpow( fac[i], P - 2 ) ;
g[0][0] = f[0][0] = 1 ;
for(re int i = 1; i <= n; ++ i) {
for(re int u = 0; u < i; ++ u) {
int v = i - u - 1 ;
rep( l, 0, u ) rep( r, 0, v )
inc( g[i][min(l, r) + 1], f[u][l] * f[v][r] % P ) ;
}
rep( k, 1, n / i ) rep( j, 1, i ) D[k][i][j] = C(g[i][j] + k - 1, k) ;
rep( j, 1, i ) drep( x, i, n ) rep( k, 1, x / i ) {
int d = D[k][i][j] ;
rep( li, k * j, x ) inc( f[x][li], f[x - i * k][li - k * j] * d % P ) ;
}
}
cout << f[n][m - 1] << endl ;
return 0 ;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号