lecture4 : Generalized Linear Model and SoftMax regression

前面的逻辑回归和线性回归其实都可以归结为一类更加广泛的模型 ： Generalized Linear Model.

首先要了解指数族分布，它们满足如下的形式：

\[p(y;\eta) = b(y)exp(\eta ^TT(y) - a(\eta)) \]

在 GLM 中，\(T(y) = y\)

指数族分布的一些性质：

1. MLE at \(\eta\) is concave, which means Negative Log Likelihood is convex
2. \(E[y;\eta] = \frac{\partial a(\eta)}{\partial \eta}\)
3. \(Var[y;\eta] = \frac{\partial ^2a(\eta)}{\partial \eta^2}\)

GLM 的一些 assumption 和 design choice：

1. \(y|x;\theta\) ~ Exp Family\((\eta)\)
2. \(\eta = \theta^Tx, \theta \in \mathbb{R}^n, x \in \mathbb{R}^n\)
3. Test time: output \(E[y|x;\theta]\), 即 \(h(x) = E[y|x;\theta]\)

GLM 的大致思路可以用下图来概括：

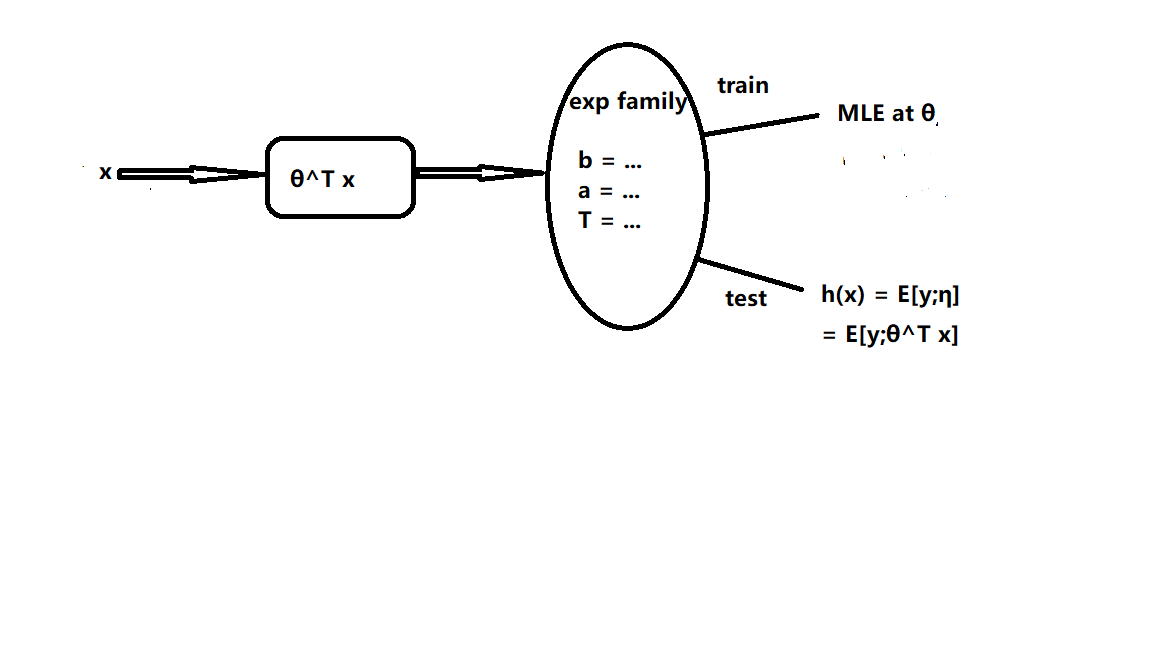
输入 \(x\) 得到 \(\eta\), 这确定了一个参数确定的指数族分布，再根据这个分布来进行预测。

线性回归和逻辑回归的 hypothesis 和 cost function 都可以由 GLM 很好地解释，分别采用正态分布和伯努利分布。

逻辑回归采用伯努利分布，可以处理二分类问题，如果待分类类别大于二，就要用到多项分布，相对应的逻辑回归的推广形式 Softmax 回归。

对于多分类问题，此时输出结果不再是一个数值，而是一个向量，第 i 个分量对应于第 i 个类别的概率。

即：

\[h(x) = \begin{bmatrix} P(y=1|x;\theta)\\ P(y = 2 | x;\theta)\\ ...\\ P(y = k|x;\theta) \end{bmatrix} = \frac{1}{\sum_{j=1}^k exp(\theta^{(j)T}x)} \begin{bmatrix} exp(\theta^{(1)T}x)\\ ...\\ exp(\theta^{(k)T}x) \end{bmatrix} \]

此处第二个等式后面提出来的系数是为了使得概率加起来为 1 的标准化因子。

\[\theta = \begin{bmatrix} \theta^{(1)} \quad \theta^{(2)} ...\quad \theta ^{(k)}\\ \end{bmatrix}, \theta^{(j)} \in \mathbb{R}^n \]

对于如何求得 \(\theta\), 和前面的线性回归和逻辑回归相同，先写出对数似然函数，然后做极大似然估计。

\[l(\theta) = \sum_{i = 1}^m log(p(y^{(i)}|x^{(i)};\theta))\\ = \sum_{i=1}^mlog(\prod_{l=1}^k \frac{exp(\theta^{(l)T}x)}{\sum_{j=1}^k exp(\theta^{(j)T}x)})^{1\{y^{(i) = l}\}}\\ = \sum_{i=1}^m \sum_{l=1}^k 1\{y^{(i)=l}\}log(\frac{exp(\theta^{(l)T}x}{\sum_{j=1}^k exp(\theta^{(j)T}x)})\\ J(\theta) = -l(\theta) \]

最优化可以使用梯度下降或者牛顿法完成。