Graph Theory - lecture_1 2021/5/6

Definition: Graph

An (undirected simple) graph is a pair \(G = (V,E)\), where \(V\) stands for the sets of vertices, and \(E\) stands for the edges set.

\( V = \{v_0,v_1,v_2,...,v_n\}\\ E \subseteq \{\{x,y\}| x,y \in V \land x != y\}\\ \)

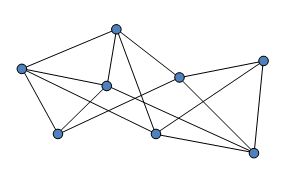
Definition : Walk,Trail and Path

Walk

Given a graph G, walk is a finite sequence of edges of the form \(\{v_0,v_1\},\{v_1,v_2\},...,\{v_{m-1},v_m\}\),here \(v_0\) is initial vertex, and \(v_m\) is called final vertex.

Trail

Trail is a walk, in which all edges are distinct, for example, in the picture above, C->B->D->B->A is a trail.(B->D and D->B we choose different edges)

Path

Path is a trail, in which all vertices are distinct, for example, in the picture above, C->A->D is a path.

Definition: Connected

A graph is connected iff \(\forall u,v \in V\), there exists a path from u to v.

Definition: Component

A component of a graph is a subgraph which is connected.

Complete

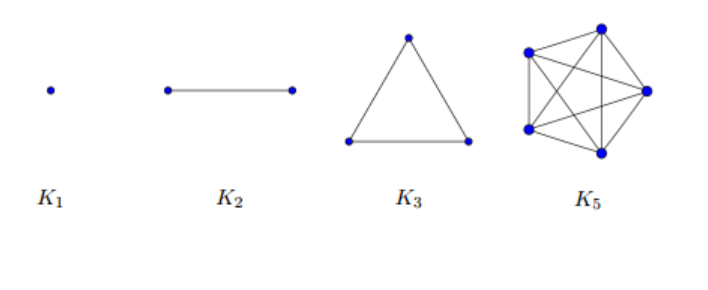
A graph is a complete graph if any two vertices in the graph are adjacent.

Definition: Closed and Cycle

Closed

If the initial vertex and the final vertex is the same in a walk, this walk is closed.

Cycle

If a path is closed, it is a cycle.

Definition: Degree

The degree of a vertex v is the number of edges whose end is v.

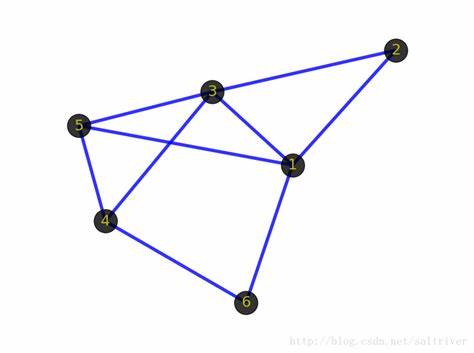
For instance, if the vertex whose label is 1 is called u, then \(deg(u) = 4\).

Definition: Eulerian Trail and Eulerian Circuit

If a trail contains all edges of a graph, the this trail is called Eulerian trail, if it is closed, then it is a Eulerian circuit.

A graph which has a Eulerian circuit is called Eulerian graph.
A graph which has a Eulerian trail but not a circuit is called semi-Eulerian graph.

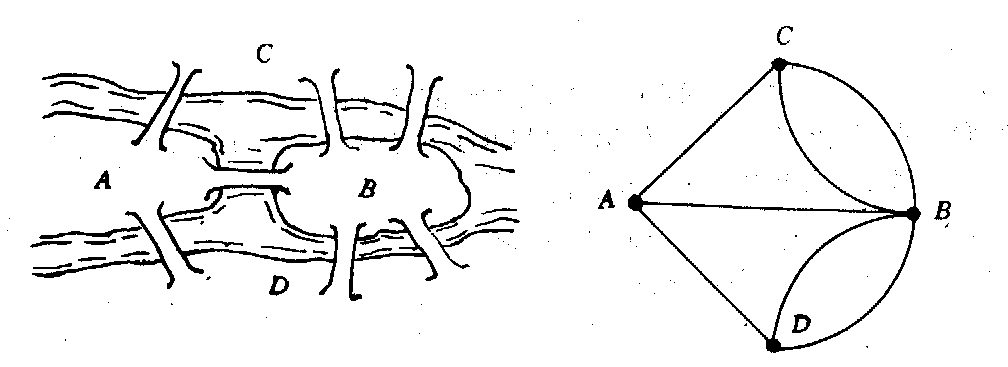
If we abstract the Seven Bridges Problem, we can find that in fact its goal is to find an Eulerian circuit.

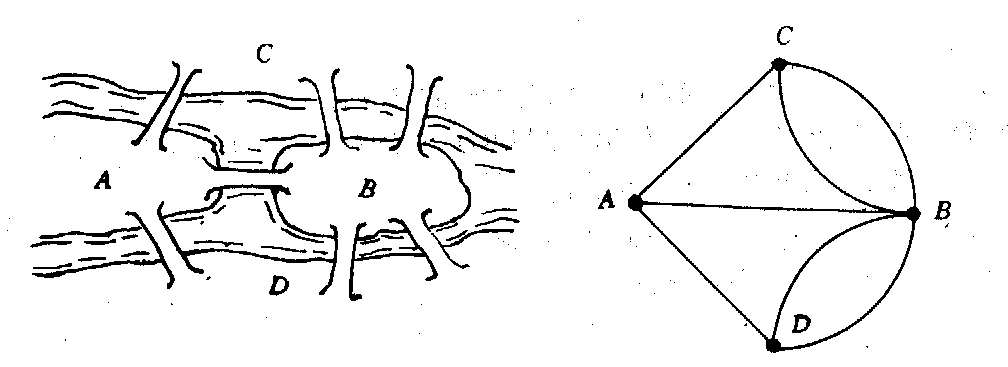
The solve of Seven Bridges Problem: Euler's Theorem

Theorem (Euler's Theorem)

A connected graph has a Eulerian circuit iff it contains no odd degree vertices. (If it contains only two odd degree vertices, it has a Eulerian trail.)

Proof:

Necessary:

if a graph has a Eulerian trail goes like this: \(v_0 -> v_1 -> ... ->v_i-> ... ->v_m\), for any \(v_i \not in\{v_0,v_m\},deg(v_i)\) is even, for it is not a start or end vertex, so is there is an edge coming in, there must be an edge going out. If \(v_0 = v_m\), then \(deg(v_i) \text{ is even}\forall v_i \in V\), otherwise, \(deg(v_0),deg(v_m)\) is odd, for they are start/end vertex.

Sufficient:

Lemma:
If all vertices of a graph has degree \(>= 2\), then there must exist a cycle in the graph.

Start Lemma Proof:

consider a maximal path: \(v_1->v_2->.....->v_k\), \(deg(v_1) >= 2\), and this is a maximal path, so there must exists at least one edge
between \(v_1\) and some \(v_i\), so there exists an cycle.

End Lemma Proof.

So we can construct an Eulerian like this.Starting from a vertex, say \(v_0\), go along with a cycle, if it contains all edges, then it is Eulerian cycle, called \(L_1\). Otherwise, delete \(L_1\), we get a subgraph G'. The original graph G is connected, so there must exist a intersection vertex of G' and \(L_1\),called \(v_i\).We start from this vertex, and continue to do the similar operation,until all edges are taken into account, getting several trails \(L_i\), then \(\bigcup L_i\) is the Eulerian cycle we want to find.

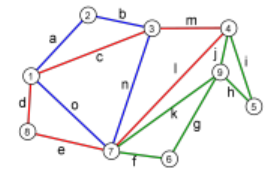
Definition: Hamiltonian Path and Hamilton Cycle

A Hamiltonian Path is a path which visits each vertex exactly once.

A Hamiltonian Cycle is a Hamiltonian Path that is a cycle.

A graph that has a Hamiltonian cycle is a Hamiltonian graph.

A graph that has a Hamiltonian path but not a cycle is a semi-Hamiltonian graph.

Remained unsolved: The Hamiltonian path/cycle problem is a NP-complete.

Typical Graph Examples

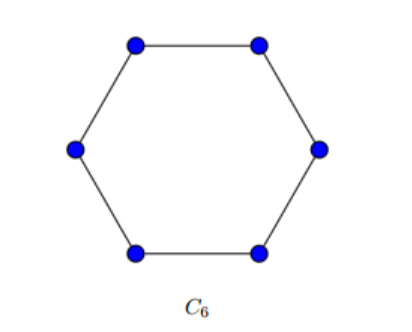
Every cycle is Hamiltonian.

A complete graph with |V| > 2 is Hamiltonian.

A complete bipartite graph \(K_{m,n}\) is Hamiltonian iff \(m = n >= 2\)

Definition: bipartite graph

A bipartite graph \(G = (U,V,E)\) is a graph whose vertices can be divided into two disjoint sets U and V such that each edge in V connects a vertex in U with one in V.

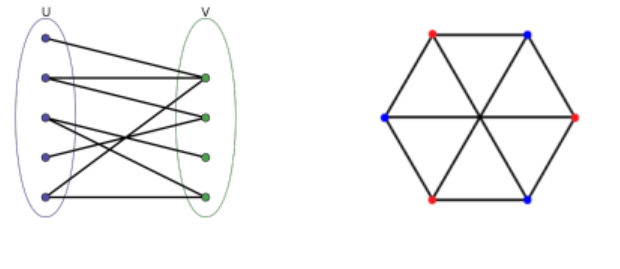
Complete bipartite graph

A complete bipartite graph is a bipartite graph in which every vertex of U is connected with every vertex of V.

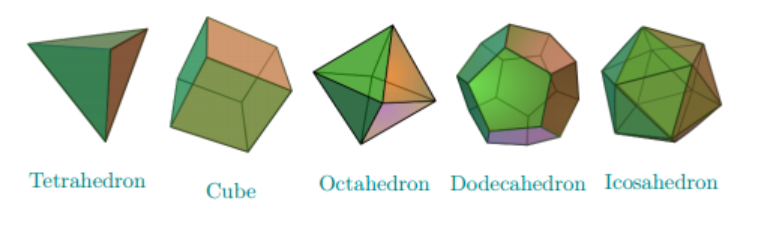
Every platonic solid considered as a graph is Hamiltonian.

A Petersen Graph is not Hamiltonian

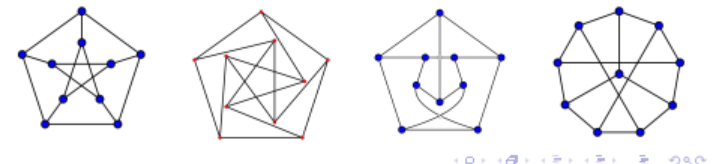
Hint: Prove by contradiction

Sufficient Condition for a Graph to be Hamiltonian:"Enough edges -> Hamiltonian"

Theorem(Ore's Theorem)

If G is a simple graph with n >= 3 vertices, then G is Hamiltonian if for each pair of non-adjacent vertices u and v, \(deg(u) + deg(v) >= n\).

Hint: Proved by contradiction and Extremality.

Theorem(Dirac's Theorem): a special case of Ore's Theorem

If G is a simple graph with n>= 3 vertices, then G is Hamiltonian if for every vertex v of G ,\(deg(v)>=n/2\).

\(δ（G）:= min\{deg(v)\}, Δ(G) := max\{deg(v)\},v \in V\)

Necessary Condition for a Graph to be Hamiltonian:"Not so connected -> Not Hamiltonian"

Theorem

If G = (V,E) is a Hamiltonian graph, S \(\subset\) G is a non-empty subset of G, then G-S has <=|S| components.

Proof:
Simply draw a graph, we can find that every component of G-S must have a edge go into it from S and a edge go out from it and go back to S, so each components at least correspond to a vertex in S, so the number of vertex is larger than that of the components.

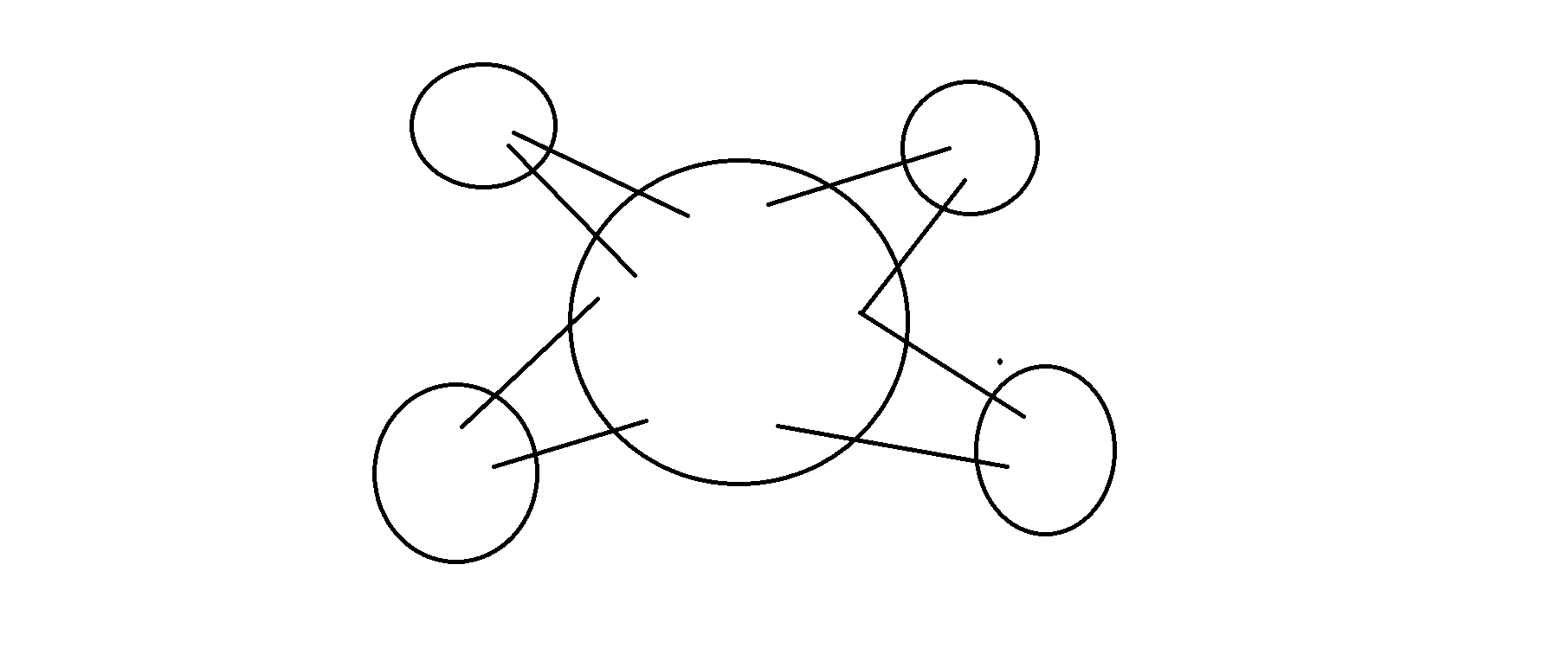
When a Hamiltonian cycle leaves a component of G-S, it can go only to a distinct vertex of S.

The condition is not sufficient, if you consider this graph.

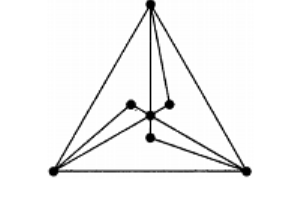
Hint:All edges incident to vertices of degree 2 must be used.

Examples of problems

Chessboard problem

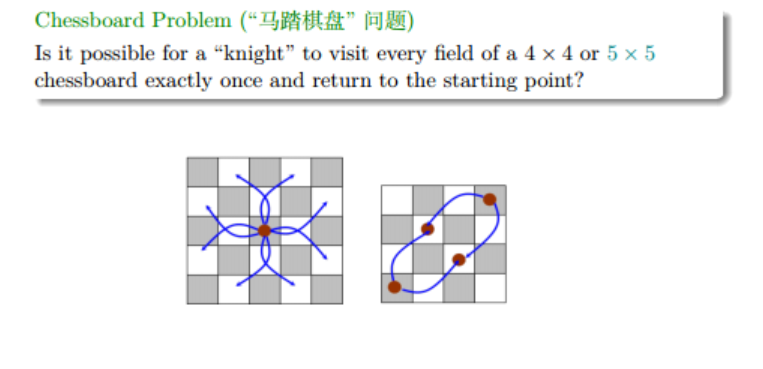
Hint: use the theorem in necessary condition.

more general version:

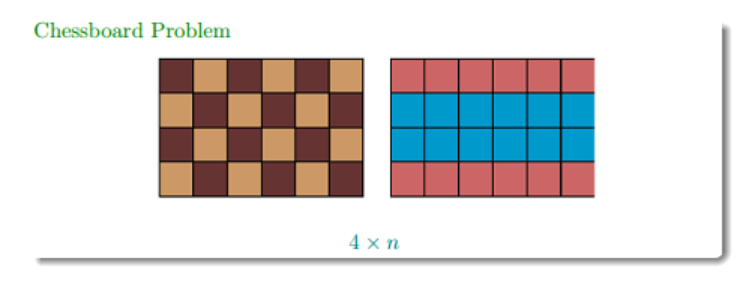
Traveling Salesman Problem

Summary

The most important things today: to examine whether a graph is Eulerian/Hamiltonian.

1. To decide whether a graph is Eulerian, use the Euler's Theorem, it is sufficient and necessary condition, just check the degree of the vertices.

2. To prove a graph is Hamiltonian, examine the sufficient condition, to prove it is not Hamiltonian, use the necessary condition.

3. Some useful proof tricks: Contradiction, induction and extremality.