Minimum Spanning Tree

Overview

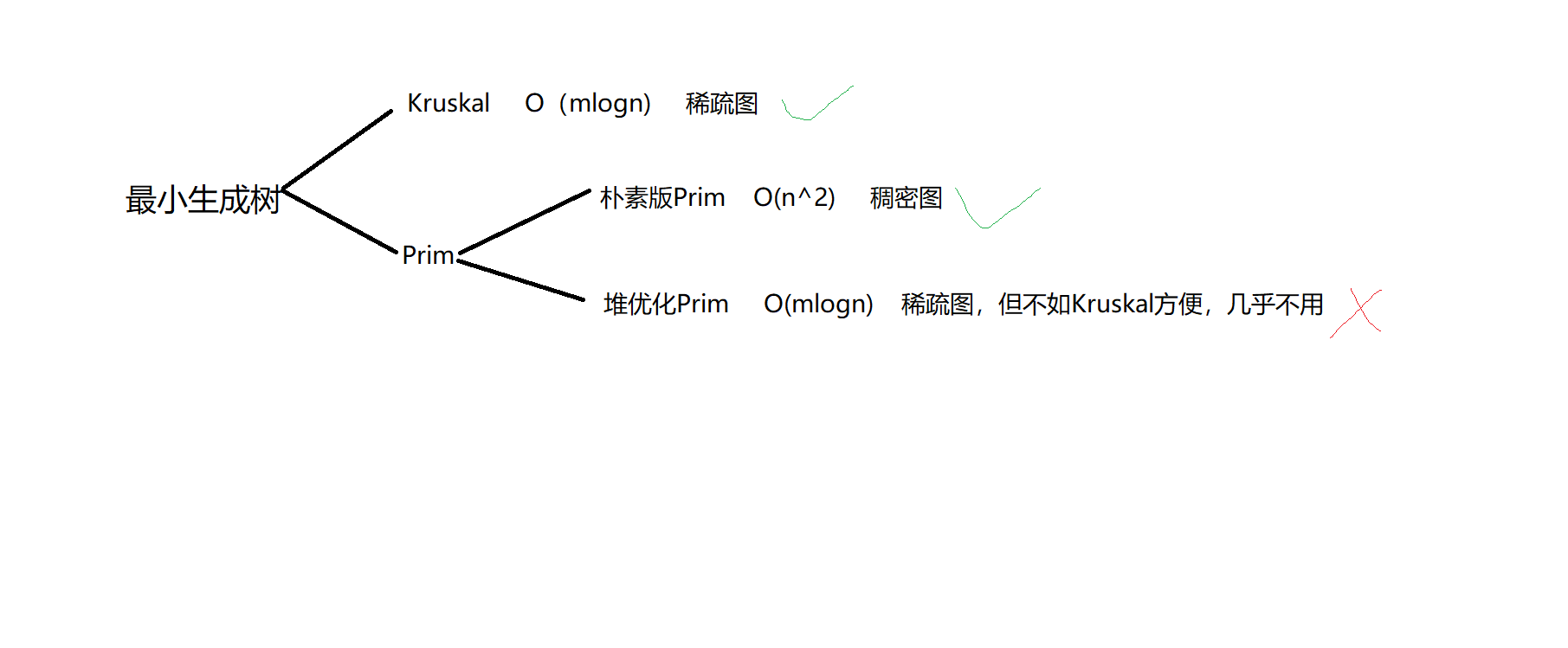
Prim's Algorithm

Prim' Algorithm 的主要思路就是维护两个集合 T, V-T，其中 V 是所有顶点组成的集合，T 是当前在正在形成的树的顶点的集合。

1. 先随便选一个点作为根节点。
2. 循环进行如下操作，直到 V = T.
   在连接 T 内顶点和 V-T 内顶点的边中选取权值最小的边 \((p_u,u)\) ,将其作为 MST 的边，并将 u 添加至 T。

代码

const int N = 120,INF = 0x3f3f3f3f;

int m[N][N],dist[N],n;//m[][]是邻接矩阵，dist[u]存的是 u 离 MST 的最近距离。

bool st[N];//标记某个点是否被加入了MST

int prim(){
    memset(dist,0x3f,sizeof dist);
    int res = 0;
    for(int i = 0; i < n ; i ++){
        //找到离当前MST最近的点
        int t = -1;
        for(int j = 1; j <= n; j ++){
            if(!st[j] && (t == -1 || dist[j] < dist[t]))t = j;
        }
        //找不到，说明不存在MST
        if(i && dist[t] == INF)return INF;
        //把这条边加入MST
        st[t] = true;
        //第一次加入点是没加入边的
        if(i) res += dist[t];
        //更新所有点到集合的距离
        for(int k = 1; k <= n ; k ++)dist[k] = min(dist[k],m[t][k]);
    }
    return res;
}

Kruskal's Algorithm

Kruskal's Algorithm 的主要思路是使用并查集来维护 MST 集合，每次寻找权最小，且加入之后不会产生回路的边。

struct Edge{
    int a,b,w;
}edges[M];

int p[N],n,m;

bool cmp(Edge u, Edge v){
    return u.w < v.w;
}
//union find 判断连通块
int find(int x){
    if(p[x] != x) p[x] = find(p[x]);

    return p[x];
}

int kruskal(){
    sort(edges,edges+m,cmp);
    int total = 0,cnt = 0;//total:sum of weight,cnt:sum of edges
    for(int i = 0; i < m ; i ++){
        int a = edges[i].a, b = edges[i].b,w = edges[i].w;

        int pa = find(a),pb = find(b);
        //说明此时两个点尚未连通，加上这条边不会成环
        if(pa != pb){
            p[pa] = pb;
            cnt++;
            total += w;
        }
    }

    if(cnt < n-1) return INF;

    return total;
}