AtCoder Beginner Contests 360~379
ABC360
E
题意
有 \(n-1\) 个白球和 \(1\) 个黑球。他们最初排成一行,黑球排在最左边。执行 \(k\) 次以下操作:
- 随机选择 2 个 \(1\) 到 \(n\) 之间的数,记为 \(a\) 和 \(b\)。如果 \(a\not=b\),把左边的第 \(a\) 个球和第 \(b\) 个球交换。
\(k\) 次操作后,黑球排在从左数的第 \(x\) 个。求 \(x\) 的期望值 \(\text{mod}\ 998244353\)。
分析
概率 DP。
设 \(f_i\) 为 \(i\) 次操作后黑球位置的期望。每次操作有 \(n^2\) 种选数的方法,其中有 \((n-1)^2+1\) 种方法不会改变黑球的位置,有 \(2n-2\) 种方法会改变黑球的位置,且黑球位置改变到其他每个位置上的概率相等。故
F
题意
有 \(N\) 个区间 \([L_i,R_i]\)。
定义满足 \(l_a<l_b<r_a<r_b\) 或 \(l_b<l_a<r_b<r_a\) 的两个区间 \([l_a,r_a]\) 和 \([l_b,r_b]\) 为交叉的。
定义 \(f(l,r)\) 为 \(N\) 个区间中,与 \([l,r]\) 交叉的区间的个数。
请求出满足 \(0\leq l<r\leq 10^9\) 的使 \(f(l,r)\) 最大的数对 \((l,r)\)。如果有多种答案,请输出 \(l\) 最小的一种。如果仍有多种答案,请输出 \(r\) 最小的一种。
分析
好题好题。(ABC346G 的加强版)
参考:https://atcoder.jp/contests/abc360/submissions/55089328
这思路太棒了。
由题意,如果 \([l,r]\) 要和 \([L,R]\) 交叉的话需满足 \(0\leq l< L\) 且 \(L<r<R\) 或 \(L<l<R\) 且 \(R<r\leq inf\)。
那么在平面直角坐标系中,有两个矩形,其中一个的顶点为 \((0,L+1)\) 和 \((L-1,R-1)\),另一个的顶点为 \((L+1,R+1)\) 和 \((R-1,inf)\),在这两个矩形之一中的任意一点 \((l,r)\) 都满足要求。如图。
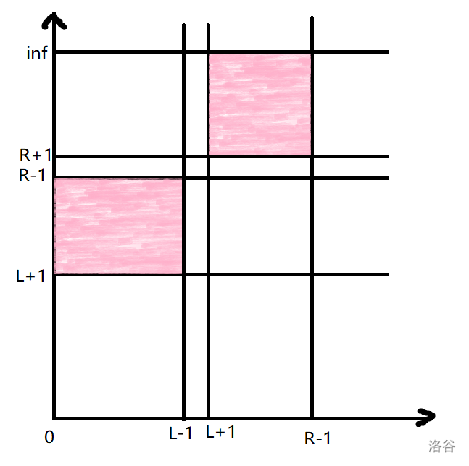
对于所有的 \(N\) 个区间 \([L_i,R_i]\),都可以产生这样的两个矩形,题目就转化成求一个点 \((l,r)\),覆盖它的矩形个数是最多的。
不是很记得扫描线怎么写了……
G
题意
有一个长度为 \(N\) 的数组 \(A\)。随机选取一个 \(1\) 到 \(N\) 之间的整数 \(x\),把 \(A_x\) 换为任意整数。求操作后 \(A\) 的最长上升子序列的最大长度。
分析
ABC365
E
题意
给你一个长度为 \(N\) 的整数序列 \(A=(A_1,\ldots,A_N)\)。求以下表达式的值:
\(\displaystyle \sum_{i=1}^{N-1}\sum_{j=i+1}^N (A_i \oplus A_{i+1}\oplus \ldots \oplus A_j)\)
分析
容易想到令 \(s_i\) 表示 \(A_1\) 到 \(A_i\) 的前缀异或和。则答案被转换为 \(\sum\limits_{i=1}^{N-1}\sum\limits_{j=i+1}^{N}s_j\oplus s_{i-1}\)。直接计算时间复杂度为 \(O(n^2)\)。
考虑每个 \(s_j\) 与前面的 \(s_{i-1}\) 对答案的贡献。两个数按位异或时,对于每一位,与自己当前位上相反会产生位权的贡献,与自己当前位上相同就不会产生贡献。那么可以开一个数组 \(cnt_{i,0/1}\) 表示有多少个数在第 \(i\) 位上为 0 或 1,每加入一个 \(s\) 就更新一次数组,同时计算答案,即把答案加上 \(\sum\limits 2^i\times cnt_{i,t_i\oplus 1}\),其中 \(t_i\) 表示 \(s\) 第 \(i\) 位上的数。
时间复杂度 \(O(n\log A)\)。
ABC366
E
题意
给你一个二维平面上的 \(N\) 点 \((x_1, y_1), (x_2, y_2), \dots, (x_N, y_N)\) 和一个非负整数 \(D\)。
求使得 \(\displaystyle \sum_{i=1}^N (|x-x_i|+|y-y_i|) \leq D\) 的整数对 \((x, y)\) 的个数。
分析
观察到 \(\sum\limits_{i=1}^{N}(|x-x_i|+|y-y_i|)\) 这个数的计算不需要依赖 \((x_i,y_i)\) 的对应关系,即可以转化成 \(\sum\limits_{i=1}^{N}|x-x_i|+\sum\limits_{i=1}^{N}|y-y_i|\)。设枚举范围的大小为 \(T\)。(\(T\) 与 \(N\) 同阶)
计算每个 \(x\) 对应的 \(\sum\limits_{i=1}^{N}|x-x_i|\) 可以从 \(O(N)\) 优化到 \(O(\log N)\)。先把所有点的横坐标排序,并求出前缀和 \(s\),对于每个 \(x\),二分找出它在横坐标中的位置,得到小于 \(x\) 的数的个数 \(t\),\(\sum\limits_{i=1}^{N}|x-x_i|=s_n-s_t-x(n-t)+xt-s_t\)。对于纵坐标同理。连同排序,预处理求出枚举范围中的每个 \(x\) 和 \(y\) 对应的贡献的时间复杂度 \(O(N\log N+N+T\log N)=O(N\log N)\)。
把上面求出的每个 \(x\) 的贡献排序,枚举 \(y\),二分求出有多少个 \(x\) 满足条件,相加即可。时间复杂度 \(O(N\log N)\)。
总时间复杂度 \(O(N\log N)\)。
注意:\(x\) 和 \(y\) 的枚举范围都是 \(-2\times 10^6\) 到 \(2\times 10^6\),存贡献的数组要开到 \(4\times 10^6\)。如果枚举范围只有 \(-10^6\) 到 \(10^6\) 会被极限数据卡掉。
F
题意
给你 \(N\) 个线性函数 \(f_1, f_2, \ldots, f_N\),其中 \(f_i(x) = A_i x + B_i\)。
求由 \(K\) 个介于 \(1\) 和 \(N\) 之间不同整数组成的序列 \(p = (p_1, p_2, \ldots, p_K)\) 的最大可能值 \(f_{p_1}(f_{p_2}(\ldots f_{p_K}(1) \ldots ))\)。
分析
套路化地,先来考虑 \(f_i(f_j(x))>f_j(f_i(x))\) 需要满足什么条件。
故使得 \(f_{p_1}(f_{p_2}(\ldots f_{p_K}(1) \ldots ))\) 最大的序列 \(p\),一定满足 \(\frac{A_{p_1}-1}{B_{p_1}}\geq\frac{A_{p_2}-1}{B_{p_2}}\geq\dots\geq\frac{A_{p_K}-1}{B_{p_K}}\)。
先将原来的函数按 \(\frac{A_i-1}{B_i}\) 从大到小排序,那么问题就转化成了求一个贡献最大的 \(K\) 长子序列。这个问题可以用动态规划解决。
设 \(dp_{i,j}\) 选到第 \(i\) 个函数,总共选了 \(j\) 个函数的最大贡献。对一个函数只有选与不选两种情况,得到状转方程:
\(dp_{i,j}=\max(dp_{i-1,j},dp_{i-1,j-1}\times A_i+B_i)\)。时间复杂度 \(O(NK)\)。
注意函数在计算的时候是从内层往外算的,所以函数的排序实际上是按 \(\frac{A_i-1}{B_i}\) 小到大排序。
ABC368
E
题意
在 Atcoder 国家,有 \(N\) 座城市,编号为 \(1\) 至 \(N\),以及 \(M\) 列火车,编号为 \(1\) 至 \(M\)。\(i\) 次列车在 \(S_i\) 时从城市 \(A_i\) 出发,在 \(T_i\) 时到达城市 \(B_i\)。
给定一个正整数 \(X_1\),求一个满足下列条件的非负整数 \(X_2,\ldots,X_M\) 的最小值 \(X_2+\ldots+X_M\) 。
- 条件对于所有满足 \(1 \leq i,j \leq M\) 的一对 \((i,j)\),如果 \(B_i=A_j\) 和 \(T_i \leq S_j\),那么 \(T_i+X_i \leq S_j+X_j\) 。
- 换句话说,对于任何一对原本可以换乘的列车,即使将每趟列车 \(i\) 的出发和到达时间延迟 \(X_i\) ,仍然可以换乘。
可以证明,这种将 \(X_2,\ldots,X_M\) 设置为 \(X_2+\ldots+X_M\) 的最小值的方法是唯一的。
分析
贪心。每一辆从 \(s\) 站点出发的列车都要等到在它之前到 \(s\) 的列车全部到了再出发。
G
题意
给定两个长度为 \(N\) 由正整数组成的序列 \(A\) 和 \(B\),有以下 \(Q\) 个操作:
-
给定两个正整数 \(i,x\),把 \(A_i\) 修改为 \(x\);
-
给定两个正整数 \(i,x\),把 \(B_i\) 修改为 \(x\);
-
给定两个正整数 \(l,r\),求出以下问题的答案:
- 把 \(v\) 设为 \(0\)。按 \(i=l,l+1,\dots,r\) 的顺序,把 \(v\) 替换为 \(\max(v+A_i,v\times B_i)\)。求最终的 \(v\) 值。 保证答案不超过 \(10^{18}\)。
分析
因为 \(v\) 不超过 \(10^{18}<2^{60}\),所以对于每次查询,乘的次数一定不超过 \(60\) 次。并且如果乘的数为 \(1\),显然选择加比选择乘更优。所以把大于 \(1\) 的 \(B_i\) 的下标都放进一个 set 里,对于每次查询,把 \([l,r]\) 区间内的那些大于 \(1\) 的 \(B_i\) 都挑出来用乘法,其他的部分都用加法。还需要一个支持单点修改、区间查询的树状数组来维护 \(A_i\) 的区间和。时间复杂度 \(O(N\log^2 N)\)。
我有一个疑惑,就是为什么用 *st.lower_bound(l) 会比用 *lower_bound(st.begin(),st.end(),l) 要快很多?
ABC369
F
题意
有一个网格,网格中有 \(H\) 行和 \(W\) 列。让 \((i,j)\) 表示从上往下数第 \(i\) 行,从左往右数第 \(j\) 列的单元格。
在这个网格中有 \(N\) 枚硬币,通过 \((R_i,C_i)\) 单元格可以拾取第 \(i\) 枚硬币。
你的目标是从 \((1,1)\) 单元格开始,反复向下或向右移动一个单元格,到达 \((H,W)\) 单元格,同时尽可能多地拾取硬币。
请找出您能拾取的最大硬币数以及能达到最大值的路径之一。
分析
赛时打算冲一下 A 六题的,结果脑子短路了,没想到怎么记录答案。不过已经是历史最好成绩了。赛后感觉这题只有绿。
显然,对于每一行,把本行要取的硬币全部取完了才能取下面的,且下面取的硬币的 \(y\) 坐标都要大于等于本行最右一枚硬币的 \(y\) 坐标。容易想到把所有硬币按 \(x\) 坐标排序,\(x\) 坐标相同的按 \(y\) 坐标排序,求 \(y\) 坐标的最长不下降子序列。
重点是输出方案。只要确定了被选出的硬币,那么输出就是一件很简单的事情。设有两枚硬币 \(u,v\) 是在路径上相邻的,那么这两枚硬币之间的路径就是 \(|x_v-x_u|\) 个向下的移动和 \(|y_v-y_u|\) 个向右的移动。
都知道动态规划能轻松解决最长不下降子序列的长度,那么怎么确定被选出的硬币是哪些呢?这在我看来是本题最大的难点。赛时就是因为没想出来这个然后寄了。
开几个名为 \(pre,g,t,d,f\) 的数组。
\(pre_i\) 表示路径中第 \(i\) 个硬币的编号。输出要用。
\(g_i\) 表示硬币 \(i\) 的上一个硬币编号。\(t_p\) 表示长度为 \(p\) 的最长不下降子序列的最后一个硬币编号。这两个数组对于求出路径至关重要。
剩下的都是常规操作:
\(d_p\) 表示长度为 \(p\) 的最长不下降子序列的最后一个硬币的 \(y\) 坐标。
\(f_i\) 表示以硬币 \(i\) 结尾的最长不下降子序列的长度。
vector<int>pre;
void putpre(int x){
if(!x)return;
putpre(g[x]);
pre.push_back(x);
}
//---------------
int p;
for(int i=1;i<=n;i++){
p=upper_bound(d,d+len+1,b[i])-d;
if(p>len)len=p;
f[i]=p;
g[i]=t[p-1];
d[p]=b[i];
t[p]=i;
}
cout<<len<<endl;
pre.push_back(0);
for(int i=1;i<=n;i++){
if(f[i]==len){
putpre(i);
break;
}
}
完整代码:
const int N=200005;
int h,w,n;
struct node{
int r,c;
}a[N];
int b[N];
bool cmp(node x,node y){
if(x.r!=y.r)return x.r<y.r;
return x.c<y.c;
}
int len,d[N],t[N],f[N],g[N];
void print(int x,int y){
for(int i=1;i<=a[y].c-a[x].c;i++)cout<<"R";
for(int i=1;i<=a[y].r-a[x].r;i++)cout<<"D";
}
vector<int>pre;
void putpre(int x){
if(!x)return;
putpre(g[x]);
pre.push_back(x);
}
int main(){
cin>>h>>w>>n;
for(int i=1;i<=n;i++){
cin>>a[i].r>>a[i].c;
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++)b[i]=a[i].c;
int p;
for(int i=1;i<=n;i++){
p=upper_bound(d,d+len+1,b[i])-d;
if(p>len)len=p;
f[i]=p;
g[i]=t[p-1];
d[p]=b[i];
t[p]=i;
}
cout<<len<<endl;
pre.push_back(0);
for(int i=1;i<=n;i++){
if(f[i]==len){
putpre(i);
break;
}
}
for(int i=1;i<=a[pre[1]].c-1;i++)cout<<"R";
for(int i=1;i<=a[pre[1]].r-1;i++)cout<<"D";
for(int i=1;i<len;i++){
print(pre[i],pre[i+1]);
}
for(int i=1;i<=w-a[pre[len]].c;i++)cout<<"R";
for(int i=1;i<=h-a[pre[len]].r;i++)cout<<"D";
return 0;
}
ABC370
D
题意
有 \(H\times W\) 的网格,初始时每个网格都是黑色。给定 \(Q\) 个操作,第 \(i\) 个操作有两个数 \(R_i,C_i\),如果 \((R_i,C_i)\) 是黑色的,就把它涂成白色。否则将其上下左右的第一个黑色格子涂成白色。
分析
本来想从 D 开题,看到这个题目就赶紧跑了。切完 ABC 回来发现题面纯纯诈骗。算了反正 ABC 题目就这个风格。
看到题第一反应是并查集,但我不太会写。然后就写了链表,写了两遍发现都假掉了,因为链表无法维护删除之后的点的邻接元素。最终用 set+二分过了。说实话并不难想。
E
题意
给定一个长度为 \(N\) 的序列 \(A=(A_1,A_2,A_3,\dots,A_N)\) 和一个整数 \(K\)。求把它分成若干个连续子序列的方案中,每一个子序列内部元素的和都不等于 \(K\) 的方案数。对 \(998244353\) 取模。
分析
赛时想出 DP 方程,但看到所剩时间不多了,就摆了,也没怎么去想优化。赛后发现比上次那道 E 还简单。
设 \(dp_n\) 为选到第 \(n\) 个数的方案数。\(dp_n=\sum\limits_{0\leq m< n}dp_m[\sum\limits_{i=m+1}^{n}A_i\not=K]\)。
前缀和优化一下:\(dp_n=\sum\limits_{0\leq m< n}dp_m[S_n-S_m\not=K]\)。
再优化一下:\(dp_n=\sum\limits_{0\leq m< n}dp_m-\sum\limits_{0\leq m< n}dp_m[S_m=S_n-K]\)。
设 \(B_k\) 为满足 \(S_i=k\) 的 \(dp_i\) 总和。可用 map 维护。
\(dp_n=\sum\limits_{0\leq m< n}dp_m-B_{S_n-K}\)。
ABC371
E
题意
给定一个长度为 \(N\) 的数列 \(A=(A_1,A_2,\dots,A_N)\)。定义 \(f(i,j)\) 为 \((A_i,A_{i+1},\dots,A_j)\) 中不同元素的种类数。求 \(\sum\limits_{i=1}^{N}\sum\limits_{j=i}^{N}f(i,j)\)。
分析
I Hate Sigma Problems.
最近的 E 好像一次比一次简单了。
考虑枚举右端点。记 \(lst_{i}\) 为 \(i\) 这个数最后一次出现的位置。每次在右端加入一个数,对前面所有左端点的影响:对 \(1\) 到 \(lst_i\) 的位置没有影响,对 \(lst_{i}+1\) 到当前位置有影响。然后我就写了线段树,其实没必要。 统计答案并更新 \(lst_i\)。
F
题意
在数轴上有 \(N\) 个人,每个人的坐标为 \(X_i\)。
你可以执行以下操作任意次:
- 选择一个人。如果目的地没有其他人,将这个人向左或向右移动 \(1\) 米。
有 \(Q\) 个任务,每个任务内容如下:
- 将第 \(T_i\) 个人移动到位置 \(G_i\)。
你需要按顺序完成所有任务,求最少进行多少次操作。
分析
联合省选 2025 D2T1 原题。
观察样例可知,移动一个人时,可能把移动方向上的连续的几个人一起移动。移动后的人的位置形成了公差为 \(1\) 的等差数列。
一个 trick:把第 \(i\) 个人的位置减去 \(i\),等差数列中的数就变成了一段相同的数。这样位置的改变就转化成了区间赋值,可以用线段树维护。
对于每次移动,在线段树上二分出离这个人最近的不需要移动的人。设他的编号为 \(j\),当前位置为 \(p_j\),额外移动的人的个数为 \(num\)。以向左移动为例,有:
又因为 \(num=T_i-j-1\),
移项得
即
向右移动同样可得 $$G_i-T_i \leq p_j-j$$。
求出 \(j\) 后,可以算出移动的次数。
ABC373
E
题意
正在举行一次选举,有 \(N\) 名候选人,编号为 \(1,2,\ldots,N\)。一共有 \(K\) 票,现在已经统计了部分的票。
到目前为止,计票结果是 \(A_i\) 票投给了编号为 \(i\) 的候选人。
计票结束后, \(i\) 号候选人 \((1 \leq i \leq N)\) 将当选,当且仅当得票多于该候选人的候选人少于 \(M\)。可有一名以上候选人当选。
求每个候选人在剩余的 \(K-\sum_{i=1}^{N}A_i\) 选票中至少需要获得多少票才能一定当选。
分析
观察到答案具有单调性,二分该候选人接下来得到的票数,然后判断。
判断运用贪心,即尽量让该候选人无法当选。
如果这个候选人加上 \(mid\) 票后,比他得票多的人还大于等于 \(M\),那么肯定不行。
否则考虑把剩下的 \(K-mid-\sum_{i-1}^{N}A_i\) 分给在前 \(M\)(排除掉该候选人)但得票小于等于 \(A_i+mid\) 的人,让他们的票数都大于 \(A_i+mid\),让该候选人落选。把所需票数和实际剩余票数进行比较。
F
题意
有 \(N\) 类物品。其中 \(i\) 类物品的体积为 \(w_i\),价值为 \(v_i\)。每种类型都有 \(10^{10}\) 个可用物品。
高桥打算选择一些物品,把它们装进一个容量为 \(W\) 的袋子里。他将选择 \(k_i\) 个 \(i\) 类型的物品的快乐值定义为 \(k_i v_i - k_i^2\)。请计算他能获得的最大快乐值。
分析
因为体积为 \(w_i\) 的物品最多放 \(\left\lfloor\frac{W}{w_i}\right\rfloor\) 件,借鉴 ABC365E,考虑使用调和级数相关的做法。
把物品按体积分类,令 \(C_{i,j}\) 为体积为 \(i\) 的物品中选 \(j\) 件的最大快乐值,这个可以优先队列+贪心预处理。然后枚举体积和每种体积选的物品个数。时间复杂度 \(O(W^2\ln W)\)。
ABC375
E
题意
有 \(N\) 人分成三个小组。
人数编号为 \(1, 2, \ldots, N\),团队编号为 \(1, 2, 3\)。目前,\(i\) 属于 \(A_i\) 小组。
每个人都有一个名为强度的值,\(i\) 的强度为 \(B_i\)。一个团队的强度被定义为其成员强度的总和。
确定是否可能有零个或更多的人交换团队,从而使所有团队的实力相等。如果可能,求最少需要多少人换队才能达到这个目的。
除了 \(1\)、\(2\)、\(3\) 队之外,您不能创建新的队。
- \(3 \leq N \leq 100\)
- \(A_i \in \lbrace 1, 2, 3 \rbrace\)
- 每个 \(x \in \lbrace 1, 2, 3 \rbrace\) 都存在一些 \(i\) 满足 \(A_i = x\)
- \(1 \leq B_i\)
- \(\displaystyle\sum_{i = 1}^{N} B_i \leq 1500\)
- 所有输入值均为整数。
分析
赛后过来看一眼这不是 DP 大水题吗。这么说这场我其实每题都会做。为什么我赛时没切,后悔莫及。
看到数据范围,可以确定 \(B_i\) 能够写进 DP 状态。然后很容易想到状态 \(dp_{i,j,k}\),最终答案为 \(dp_{N,\frac{S}{3},\frac{S}{3}}\)。状态是啥就懒得写了,反正赛后一看就出来了。
G
题意
在 AtCoder 国家中,有 \(N\) 座城市,编号为 \(1\) 至 \(N\),以及 \(M\) 条道路,编号为 \(1\) 至 \(M\)。
道路 \(i\) 双向连接城市 \(A_i\) 和 \(B_i\),长度为 \(C_i\)。
对于每个 \(i = 1, \ldots, M\),判断下列两个值是否不同。
- 当所有道路都可以通行时,从城市 \(1\) 到城市 \(N\) 的最短距离
- 当除道路 \(i\) 之外的道路 \(M - 1\) 均可通行时,从城市 \(1\) 到城市 \(N\) 的最短距离
如果在其中一种情况下可以从城市 \(1\) 到达城市 \(N\),而在另一种情况下则不能,则这两个值被认为是不同的。
分析
首先建出最短路图。对于每一条边,检查它是否是最短路图的割边即可。
最短路图的建法:
对于无向图,从 \(1\) 和 \(N\) 号点分别跑一次最短路,对于每条边 \((u,v)\),若 \(dis_u+w+dis2_v=dis_n\) 或 \(dis_v+w+dis2_u=dis_n\),则这条边在最短路图上。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号