排序算法

排序算法

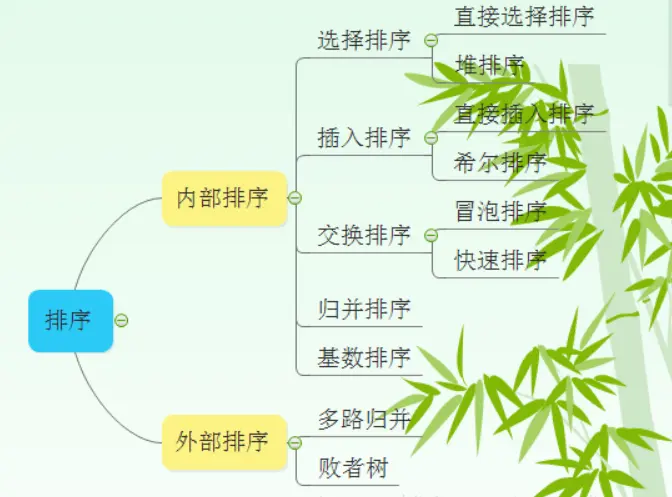
1. 排序的分类

• 内部排序

  指将需要处理的所有数据都加载到内部存储器中进行排序。

• 外部排序法

  数据量过大时，无法全部加载到内存中，需要借助外部存储进行排序。

2. 算法的时间复杂度

2.1 概述

一般情况下，算法中的基本操作语句的重复执行次数是问题规模n的某个函数，用T(n)来表示。若有某个辅助函数f(n)，可以使得当n趋近于无穷大时，使得T(n)/f(n)的极限值为不等于0的常数，则称f(n)是T(n)的同数量级函数。记作T(n) = O(f(n))，称O(f(n))为算法的渐进时间复杂度，简称时间复杂度。

2.2 估算方法

• 用常数1代替运行时间中的所有加法常数，也即常数项可忽略；eg.T(n) = 2n²+7n+6 => T(n) = 2n²+7n+1
• 修改后的运行次数函数中，只保留最高阶项，也即低次项可忽略；eg.T(n) = 2n²+7n+1 => T(n) = 2n²
• 去除最高阶项的系数，也即系数可忽略。eg.T(n) = 2n² => T(n) = n² => O(n²)

2.3 常见的时间复杂度

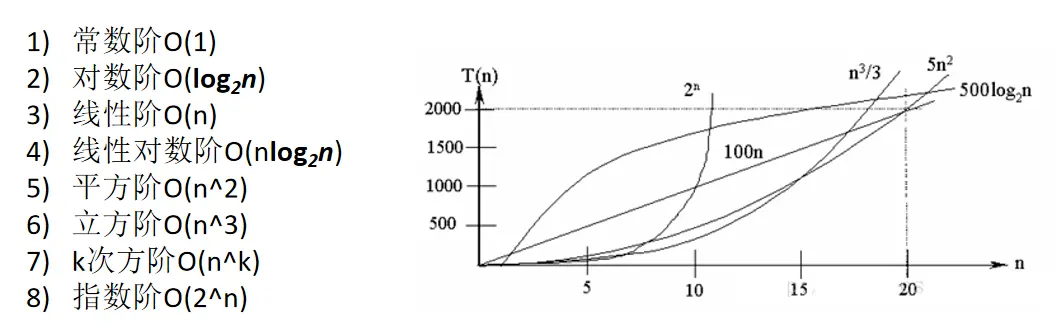
说明：常见的算法时间复杂度由小到大排序结果依次为上述的1-8的顺序，应当尽可能避免使用指数阶的算法。

2.4 平均时间复杂度和最坏时间复杂度

• 平均时间复杂度是指所有可能的输入实例均以等概率出现的情况下，该算法的运行时间；
• 最坏情况下的时间复杂度称为最坏时间复杂度。一般讨论的时间复杂度即为最坏时间复杂度；
• 平均时间复杂度和最坏时间复杂度是否一致与具体算法有关。