递归算法

递归算法

1. 何为递归

简而言之，就是方法自己调用自己，在每一次调用时传入不同的变量。递归有助于编程者在解决复杂问题的同时，让代码变得更加简洁。

2. 递归的应用场景

• 各种数学问题，eg.8皇后问题、汉诺塔、阶乘问题、迷宫问题、球和篮子的问题等；
• 各种算法中也经常用到递归的思想，eg.快排、归并排序、二分查找、分治算法等；
• 将用栈解决的问题，使用递归代码会比较简洁。

3. 递归需要遵守的重要规则

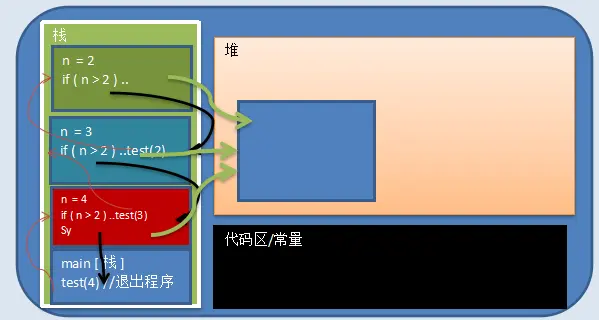
• 执行一个方法时，就创建一个新的受保护的独立空间（栈空间）；
• 每一个方法中的局部变量都是独立的，不会相互影响，eg.上图中的test方法中的变量n；
• 如果方法中使用的是引用类型变量（而非基本类型变量，eg.数组），就会共享该引用类型的数据（eg.上图堆中的变量/对象）;
• 递归必须向退出递归的条件逼近，否则就是无限递归，出现StackOverflowError，栈溢出；
• 当一个方法执行完毕，或者遇到return，就会返回。遵循谁调用，就将结果返回给谁，同时当方法执行完毕或返回时，该方法也即执行完毕；
• 需要注意的是，在设计递归算法时需要考虑以下几点：
  • 明确递归的终止条件；
  • 给出递归终止时的处理办法；

4. 迷宫回溯问题

4.1 分析

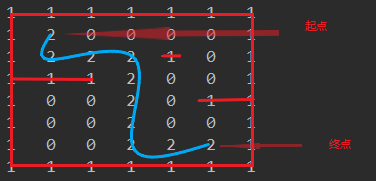
迷宫回溯问题是指在一个设置了障碍墙的迷宫中，能否找到一条到达指定目标位置的通路的问题。用二维数组表示迷宫，每个位置都有四种情况：0表示该点未走过，1表示该点为障碍墙，2表示该点可走通，3表示该点走过但走不通。

4.2 代码实现

package com.algorithm;

/**
 * @author SnkrGao
 * @create 2023-04-08 14:10
 */
public class MazeBackTracking {

    public static void main(String[] args) {
        int[][] maze = GenerateMaze.getMaze(8, 7);
        GenerateMaze.setBarriers(maze, 3, 1);
        GenerateMaze.setBarriers(maze, 3, 2);
        GenerateMaze.setBarriers(maze, 2, 4);
        GenerateMaze.setBarriers(maze, 4, 5);

        BackTracking.findWays(maze, 1, 1);
        BackTracking.iteratorAll(maze);

    }
}

class GenerateMaze {
    public static int[][] getMaze(int rows, int cols) {
        int[][] maze = new int[rows][cols];
        // 迷宫外围全置1，表示墙
        for (int i = 0; i < rows; i++) {
            maze[i][0] = 1;
            maze[i][cols - 1] = 1;
        }

        for (int i = 0; i < cols; i++) {
            maze[0][i] = 1;
            maze[rows - 1][i] = 1;
        }

        return maze;
    }

    public static void setBarriers(int[][] maze, int xBarrier, int yBarrier) {
        // 将maze[x][y]处设置为墙
        maze[xBarrier][yBarrier] = 1;
    }
}

class BackTracking {

    public static boolean findWays(int[][] maze, int curRow, int curCol) {
        if (maze[6][5] == 2) { // 递归终止条件，说明找到通路
            return true;
        } else {
            if (maze[curRow][curCol] == 0) { // 说明该位置还没走过
                maze[curRow][curCol] = 2; // 先假设该位置能走通
                // 设置策略为：下->右->上->左
                if (findWays(maze, curRow + 1, curCol)) {
                    return true;
                } else if (findWays(maze, curRow, curCol + 1)) {
                    return true;
                } else if (findWays(maze, curRow - 1, curCol)) {
                    return true;
                } else if (findWays(maze, curRow, curCol - 1)) {
                    return true;
                } else {
                    maze[curRow][curCol] = 3; // 表示该点走过但走不通
                    return false;
                }
            } else {
                return false;
            }
        }
    }

    public static void iteratorAll(int[][] maze) { // 打印迷宫
        for (int i = 0; i < maze.length; i++) {
            for (int j = 0; j < maze[i].length; j++) {
                System.out.print(maze[i][j] + "\t");
            }
            System.out.println();
        }
    }
}

4.3 运行结果分析