噪声相关笔记
噪声： 不期望接收到的信号（相对于期望接收到的信号）
白噪声： 功率谱密度为常数的随机信号或随机过程，功率谱密度在整个频域内均匀分布的噪声。此信号在各个频段上的功率是一样的。相对的，其它不具有这一性质的噪声信号（功率谱密度不均匀）被称为有色噪声。（频谱是一个常数）
高斯噪声： 是一种服从高斯分布的随机噪声。
高斯白噪声： 幅度统计规律服从高斯分布而功率谱为常数的噪声。仿真时经常采用高斯白噪声，这是因为实际系统（包括雷达和通信系统等大多数电子系统）中的主要噪声是热噪声，而热噪声是典型的高斯白噪声，高斯噪声下的理想系统都是线性系统
白噪声不必服从高斯分布，高斯分布的噪声不一定是白噪声
加性噪声： 一般指热噪声、散弹噪声等。它们与信号的关系是相加，不管有没有信号，噪声都存在。一般通信中把加性随机性看成是系统的背景噪声。
乘性噪声： 一般由信道不理想引起的。它们与信号的关系是相乘，信号在，噪声在；信号不在，噪声也就消失。乘性随机性看成是系统的时变性或者非线性造成的。乘性噪声普遍存在于现实世界的图像应用当中。
- 高斯噪声：是一种随机噪声，其时域内信号幅度（实数域是绝对值，复数域是模）的统计规律服从高斯分布
- 白噪声：白是指该信号的功率谱在整个频域内为常数的噪声，其傅里叶反变换是单位冲击函数，其自相关函数也是冲击函数（说明这种信号只与自己相关，与它的时延信号就不相关）
高斯白噪声和高斯有色噪声的区别：高斯有色噪声其分布是高斯的，但是它的频谱在整个频域内不是一个常数，或者说，对高斯信号采样的时候不是随机采样的，而是按照某种规律来采样的。理想的噪声时具有无限带宽，因而其能量是无限大，但是在现实世界是不可能存在的。一般的，只要一个噪声过程所具有的频谱宽度远远大于它所作用的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，就可以当做白噪声处理。一般将噪声当做白噪声，是因为一般生活中的噪声由热噪声产生，其为高斯白噪声。
时域特性与频域特性共同决定了噪声的特性。时域特性与频域特性相互独立，也即是说，时域特性由概率分布（高斯还是均匀分布还是其他分布）决定的，频域特性（白与不白）则由频带宽度决定的。
功率谱是功率谱密度的简称。
从统计角度出发：当这个随机变量（噪声），服从均值为0，方差为σ2的正态分布（即二阶中心矩），即为标准正态分布。
当均值为0时，二阶中心距等于二阶原点矩。而二阶原点矩就是一个信号的功率。
功率谱是功率的傅里叶变换。高斯白噪声的功率是σ2，变换前后分别是，时域的δ脉冲信号（脉冲的强度是σ2）和在频域的一条直线（即功率谱是常数）
功率谱密度相关方法的MATLAB实现（谱估计方法）
1.基本方法
周期图法是直接将信号的采样数据x(n)进行Fourier变换求取功率谱密度估计的方法。假定有限长随机信号序列为x(n)。它的Fourier变换和功率谱密度估计存在下面的关系：
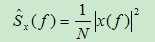，f=kΔf
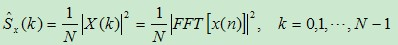
式中，N为随机信号序列x(n)的长度。
其中，FFT[x(n)]为对序列x(n)的Fourier变换，由于FFT[x(n)]的周期为N，求得的功率谱估计以N为周期，因此这种方法称为周期图法。下面用例子说明如何采用这种方法进行功率谱。（|X(k)|=FFT[x(n)]）
用有限长样本序列的Fourier变换来表示随机序列的功率谱，只是一种估计或近似，不可避免存在误差。为了减少误差，使功率谱估计更加平滑，可采用分段平均周期图法（Bartlett法）、加窗平均周期图法（Welch法）等方法加以改进。
2.分段平均周期图法
将信号序列x(n)，n=0,1,…,N-1，分成互不重叠的P个小段，每小段由m个采样值，则P*m=N。对每个小段信号序列进行功率谱估计，然后再取平均作为整个序列x(n)的功率谱估计。
平均周期图法还可以对信号x(n)进行重叠分段，如按2:1重叠分段，即前一段信号和后一段信号有一半是重叠的。对每一小段信号序列进行功率谱估计，然后再取平均值作为整个序列x(n)的功率谱估计。这两种方法都称为平均周期图法，一般后者比前者好。程序见下，上图采用不重叠分段法的功率谱估计，下图为2:1重叠分段的功率谱估计，可见后者估计曲线较为平滑。与上例比较，平均周期图法功率谱估计具有明显效果（涨落曲线靠近0dB）。
3.加窗平均周期图法
加窗平均周期图法是对分段平均周期图法的改进。在信号序列x(n)分段后，用非矩形窗口对每一小段信号序列进行预处理，再采用前述分段平均周期图法进行整个信号序列x(n)的功率谱估计。由窗函数的基本知识可知，采用合适的非矩形窗口对信号进行处理可减小“频谱泄露”，同时可增加频峰的宽度，从而提高频谱分辨率。
上程序采用无重叠数据分段的加窗平均周期图法进行功率谱估计，而程序采用重叠数据分段的加窗平均周期图法进行功率谱估计，显然后者是更佳的，信号谱峰加宽，而噪声谱均在0dB附近，更为平坦（注意采用无重叠数据分段噪声的最大的下降分贝数大于5dB，而重叠数据分段周期图法噪声的最大下降分贝数小于5dB）。
4.Welch法估计及其MATLAB函数
Welch功率谱密度就是用改进的平均周期图法来求取随机信号的功率谱密度估计的。Welch法采用信号重叠分段、加窗函数和FFT算法等计算一个信号序列的自功率谱估计(PSD如上例中的下半部分的求法)和两个信号序列的互功率谱估计（CSD）
MATLAB信号处理工具箱函数提供了专门的函数PSD和CSD自动实现Welch法估计，而不需要自己编程。
信号自功率谱密度：
[Pxx,f]=psd(x,Nfft,Fs,window,Noverlap,’dflag’)
式中，x为信号序列；Nfft为采用的FFT长度。这一值决定了功率谱估计速度，当Nfft采用2的幂时，程序采用快速算法；Fs为采样频率；Window定义窗函数和x分段序列的长度。窗函数长度必须小于或等于Nfft，否则会给出错误信息；Noverlap为分段序列重叠的采样点数（长度），它应小于Nfft;dflag为去除信号趋势分量的选择项：’linear’,去除线性趋势分量，’mean’去除均值分量，’none’不做去除趋势处理。Pxx为信号x的自功率谱密度估计。f为返回的频率向量，它和Pxx对应，并且有相同长度
缺省值为：Nfft=min(256,length(x)),Fs=2Hz, window=hanning(Nfft),noverlap=0. 若x是实序列，函数psd仅计算频率为正的功率
[Pxx,Pxxc,f]=psd(x,Nfft,Fs,window,Noverlap,p)
式中，p为置信区间，0<=p<=1。
置信区间：用中括号[a,b]表示样本估计总体平均值误差范围的区间。a、b的具体数值取决于你对于”该区间包含总体均值”这一结果的可信程度，因此[a,b]被称为置信区间。
互功率谱密度
[Pxy[,f]]=csd(x,y,Nfft,Fs,window,Noverlap,’dflag’)
[Pxy,Pxyc[,f]]=csd(x,y,Nfft,Fs,window,Noverlap,p)
这里，x,y为两个信号序列；Pxy为x,y的互功率谱估计；其他参数的意义同自功率谱函数psd。
可以看到，两个白噪声信号的互功率谱（上图）杂乱无章，看不出周期成分，大部分功率谱在-5dB以下。然而白噪声与带有噪声的周期信号的功率谱在其周期（频率为1000Hz）处有一峰值，清楚地表明了周期信号的周期或频率。因此，利用未知信号与白噪声信号的互功率谱也可以检测未知信号中所含有的频率成分。
5.多窗口法（Multitaper method,MTM）
利用多个正交窗口（Tapers）获得各自独立的近似功率谱估计，然后综合这些估计得到一个序列的功率谱估计。相对于普通的周期图法，这种功率谱估计具有更大的自由度，并在估计精度和估计波动方面均有较好的效果。普通的功率谱估计只利用单一窗口，因此在序列始端和末端均会丢失相关信息，而且无法找回。而MTM法估计增加窗口使得丢失的信息尽量减少。
MTM法简单地采用一个参数：时间带宽积(Time-bandwidth product)NW，这个参数用以定义计算功率谱所用窗的数目，为2*NW-1。NW越大，功率谱计算次数越多，时间域分辨率越高，而频率域分辨率降低，使得功率谱估计的波动减小。随着NW增大，每次估计中谱泄漏增多，总功率谱估计的偏差增大。对于每一个数据组，通常有一个最优的NW使得在估计偏差和估计波动两方面求得折中，这需要在程序中反复调试来获得。
MATLAB信号处理工具箱中函数PMTM就是采用MTM法估计功率谱密度。函数调用格式为：
[Pxx,]]=pmtm(x,nw,Nfft,Fs)
式中，x为信号序列；nw为时间带宽积，缺省值为4。通常可取2，5/2，3，7/2；Nfft为FFT长度；Fs为采样频率。
上面的函数还可以通过无返回值而绘出置信区间，如pmtm(x,nw,Nfft,Fs,’option’,p)绘制带置信区间的功率谱密度估计曲线，0<=p<=1。
6.最 大 熵 法（Maxmum entropy method， MEM法）
如上所述，周期图法功率谱估计需要对信号序列“截断”或加窗处理，其结果是使估计的功率谱密度为信号序列真实谱和窗谱的卷积，导致误差的产生。
最大熵功率谱估计的目的是最大限度地保留截断后丢失的“窗口”以外信号的信息，使估计谱的熵最大。主要方法是以已知的自相关序列rxx(0),rxx(1),…,rxx(p)为基础，外推自相关序列rxx(p+1),rxx(p+2),…，保证信息熵最大。
最大熵功率谱估计法假定随机过程是平稳高斯过程，可以证明，随机信号的最大熵谱与AR自回归（全极点滤波器）模型谱是等价的。
MATLAB信号处理工具箱提供最大熵功率谱估计函数pmem，其调用格式为：
[Pxx,f,a]=pmem(x,p,Nfft,Fs,’xcorr’)
式中，x为输入信号序列或输入相关矩阵；p为全极点滤波器阶次；a为全极点滤波器模型系数向量；’xcorr’是把x认为是相关矩阵。
比较最大熵功率谱估计(MEM)和改进的平均周期图功率谱估计，可见，MEM法估计的功率谱曲线较光滑。在这一方法中，MEM法选定全极点滤波器的阶数取得越大，能够获得的窗口外的信息越多，但计算量也越大，需要根据情况折中考虑。
7.多信号分类法
MATLAB信号处理工具箱还提供另一种功率谱估计函数pmusic。该函数执行多信号分类法（multiple signal classification， Music法)。将数据自相关矩阵看成由信号自相关矩阵和噪声自相关矩阵两部分组成，即数据自相关矩阵R包含有两个子空间信息：信号子空间和噪声子空间。这样，矩阵特征值向量（Eigen vector）也可分为两个子空间：信号子空间和噪声子空间。为了求得功率谱估计，函数pmusic计算信号子空间和噪声子空间的特征值向量函数，使得在周期信号频率处函数值最大，功率谱估计出现峰值，而在其他频率处函数值最小。其调用格式为：
[Pxx,f,a]=pmusic(x,p,thresh,Nfft,Fs,window,Noverlap)
式中,x为输入信号的向量或矩阵；p为信号子空间维数；thresh为阈值，其他参数的意义与函数psd相同。
噪声强度=噪声功率
一点说明，对高斯白噪声，其方差和功率（单位为W）是一样的。因此，对方差，要做的只是将w变换成dbw，即dbw=10log（w）。
Matlab产生高斯白噪声的两个函数
- WGN：产生高斯白噪声
- AWGN：在某一信号中加入高斯白噪声
y = wgn(m,n,p);%%产生一个m行n列的高斯白噪声的矩阵，p以dBW为单位制定信号的强度 ,等同于sqrt(10^(p/10))*randn(m,n)
y = awgn(x,SNR);%%在信号x中加入高斯白噪声。信噪比SNR以dB为单位。x的强度假定为0dBW。如果x是复数，就加入复噪声 sqrt(noisePower)*randn(n,1)
matlab里面，randn(m,n)生成标准正态分布的伪随机数（均值为0，方差为1），rand(m,n)生成均匀分布的伪随机数，分布在（0~1）之间；
功率谱密度相关方法的MATLAB实现
%%
%分段平均周期图法（Bartlett法）
%运用信号不重叠分段估计功率谱
clc;close all;clear all;
Nsec=256;
N=1024;
y=wgn(N,1,10*log10(1));
sigLength=length(y);
Fs=1000;
% n=0:sigLength-1;t=n/Fs; %数据点数，分段间隔，时间序列
pxx1=abs(fft(y(1:256),Nsec).^2)/Nsec; %第一段功率谱
pxx2=abs(fft(y(257:512),Nsec).^2)/Nsec; %第二段功率谱
pxx3=abs(fft(y(515:768),Nsec).^2)/Nsec; %第三段功率谱
pxx4=abs(fft(y(769:1024),Nsec).^2)/Nsec; %第四段功率谱
Pxx=10*log10((pxx1+pxx2+pxx3+pxx4)/4); %平均得到整个序列功率谱
f=(0:length(Pxx)-1)*Fs/length(Pxx); %给出功率谱对应的频率
%%plot(f(1:Nsec/2),Pxx(1:Nsec/2)); %绘制功率谱曲线
figure,plot(f(1:Nsec/2),Pxx(1:Nsec/2)); %绘制功率谱曲线
xlabel('频率/Hz');ylabel('功率谱 /dB');
title('平均周期图(无重叠) N=4*256');
grid on
%%
%运用信号重叠分段估计功率谱
pxx1=abs(fft(y(1:256),Nsec).^2)/Nsec; %第一段功率谱
pxx2=abs(fft(y(129:384),Nsec).^2)/Nsec; %第二段功率谱
pxx3=abs(fft(y(257:512),Nsec).^2)/Nsec; %第三段功率谱
pxx4=abs(fft(y(385:640),Nsec).^2)/Nsec; %第四段功率谱
pxx5=abs(fft(y(513:768),Nsec).^2)/Nsec; %第五段功率谱
pxx6=abs(fft(y(641:896),Nsec).^2)/Nsec; %第六段功率谱
pxx7=abs(fft(y(769:1024),Nsec).^2)/Nsec; %第七段功率谱
Pxx=10*log10((pxx1+pxx2+pxx3+pxx4+pxx5+pxx6+pxx7)/7); %功率谱平均并转化为dB
f=(0:length(Pxx)-1)*Fs/length(Pxx); %频率序列
figure,plot(f(1:Nsec/2),Pxx(1:Nsec/2)); %绘制功率谱曲线
xlabel('频率/Hz'); ylabel('功率谱/dB');
title('平均周期图(重叠一半) N=1024');
grid on
%%
w=hanning(256); %采用的窗口数据
%采用不重叠加窗方法的功率谱估计
pxx1=abs(fft(w.*y(1:256),Nsec).^2)/norm(w)^2; %第一段加窗振幅谱平方
pxx2=abs(fft(w.*y(257:512),Nsec).^2)/norm(w)^2; %第二段加窗振幅谱平方
pxx3=abs(fft(w.*y(513:768),Nsec).^2)/norm(w)^2; %第三段加窗振幅谱平方
pxx4=abs(fft(w.*y(769:1024),Nsec).^2)/norm(w)^2; %第四段加窗振幅谱平方
Pxx=10*log10((pxx1+pxx2+pxx3+pxx4)/4); %求得平均功率谱，转换为dB
f=(0:length(Pxx)-1)*Fs/length(Pxx); %求得频率序列
figure
subplot(2,1,1),plot(f(1:Nsec/2),Pxx(1:Nsec/2)); %绘制功率谱曲线
xlabel('频率/Hz');ylabel('功率谱/dB');
title('加窗平均周期图(无重叠) N=4*256');
grid on
%采用重叠加窗方法的功率谱估计
pxx1=abs(fft(w.*y(1:256),Nsec).^2)/norm(w)^2; %第一段加窗振幅谱平方
pxx2=abs(fft(w.*y(129:384),Nsec).^2)/norm(w)^2; %第二段加窗振幅谱平方
pxx3=abs(fft(w.*y(257:512),Nsec).^2)/norm(w)^2; %第三段加窗振幅谱平方
pxx4=abs(fft(w.*y(385:640),Nsec).^2)/norm(w)^2; %第四段加窗振幅谱平方
pxx5=abs(fft(w.*y(513:768),Nsec).^2)/norm(w)^2; %第五段加窗振幅谱平方
pxx6=abs(fft(w.*y(641:896),Nsec).^2)/norm(w)^2; %第六段加窗振幅谱平方
pxx7=abs(fft(w.*y(769:1024),Nsec).^2)/norm(w)^2; %第七段加窗振幅谱平方
Pxx=10*log10((pxx1+pxx2+pxx3+pxx4+pxx5+pxx6+pxx7)/7);%平均功率谱转换为dB
f=(0:length(Pxx)-1)*Fs/length(Pxx); %频率序列
subplot(2,1,2),plot(f(1:Nsec/2),Pxx(1:Nsec/2)); %绘制功率谱曲线
xlabel('频率/Hz');ylabel('功率谱/dB');
title('加窗平均周期图(重叠一半)N=1024');
grid on
%4分段平均周期图法（hanning窗）
Nsec=256;
% n=0:sigLength-1;
% t=n/Fs;
w=hanning(256);
Pxx1=abs(fft(w.*y(1:256),Nsec).^2)/Nsec;
Pxx2=abs(fft(w.*y(257:512),Nsec).^2)/Nsec;
Pxx3=abs(fft(w.*y(513:768),Nsec).^2)/Nsec;
Pxx4=abs(fft(w.*y(769:1024),Nsec).^2)/Nsec;
Pxx=10*log10((Pxx1+Pxx2+Pxx3+Pxx4)/4);
f=(0:length(Pxx)-1)*Fs/length(Pxx);
figure
subplot(2,1,1)
plot(f(1:Nsec/2),Pxx(1:Nsec/2))
xlabel('频率/Hz');ylabel('功率谱/dB');
title('Averaged Modified Periodogram (none overlap) N=4*256');
grid
%4分段（2：1重叠）平均周期图法（hanning窗）
Nsec=256;
% n=0:sigLength-1;
%
% t=n/Fs;
w=hanning(256);
Pxx1=abs(fft(w.*y(1:256),Nsec).^2)/Nsec;
Pxx2=abs(fft(w.*y(129:384),Nsec).^2)/Nsec;
Pxx3=abs(fft(w.*y(257:512),Nsec).^2)/Nsec;
Pxx4=abs(fft(w.*y(385:640),Nsec).^2)/Nsec;
Pxx5=abs(fft(w.*y(513:768),Nsec).^2)/Nsec;
Pxx6=abs(fft(w.*y(641:896),Nsec).^2)/Nsec;
Pxx7=abs(fft(w.*y(769:1024),Nsec).^2)/Nsec;
Pxx=10*log10((Pxx1+Pxx2+Pxx3+Pxx4+Pxx5+Pxx6+Pxx7)/7);
f=(0:length(Pxx)-1)*Fs/length(Pxx);
subplot(2,1,2);plot(f(1:Nsec/2),Pxx(1:Nsec/2))
xlabel('频率/Hz');ylabel('Power Spectrum (dB)');
title('Averaged Modified Periodogram (half overlap) N=1024');
grid
%PSD_WELCH方法
%采样频率
Nfft=1024;%n=0:sigLength-1;t=n/Fs; %数据长度、时间序列
window=hanning(256); %选用的窗口
noverlap=128; %分段序列重叠的采样点数（长度）
dflag='none'; %不做趋势处理
probability=1;
% [Pxx,f]=pwelch(y,window,noverlap,Nfft,Fs,'ConfidenceLevel',probability); %功率谱估计,并以0.95的置信度给出置信区间，无返回值是绘制出置信区间,[pxx,f] = pwelch(x,window,noverlap,f,fs)
[Pxx,f]=pwelch(y,window,noverlap,Nfft,Fs);
figure
plot(f,10*log10(Pxx)); %绘制功率谱
xlabel('频率/Hz');ylabel('功率谱/dB');
title('PSD—Welch方法'); grid on
%%
%最大熵法（MEM法）
window=hanning(256); %采用窗口
[Pxx1,f]=pmem(y,20,Nfft,Fs); %采用最大熵法，采用滤波器阶数14，估计功率谱
figure,subplot(2,1,1),plot(f,10*log10(Pxx1)); %绘制功率谱
xlabel('频率/Hz');ylabel('功率谱/dB');
title('最大熵法 Order=20原始信号功率谱');grid on
[Pxx1,f]=pmem(y,20,Nfft,Fs); %采用最大熵法，采用滤波器阶数14，估计功率谱
subplot(2,1,2),plot(f,10*log10(Pxx1)); %绘制功率谱
xlabel('频率/Hz');ylabel('功率谱/dB');axis([0 4000 -20 0])
title('最大熵法 Order=20滤波后的信号功率谱');grid on
%%
%用多窗口法(MTM)
[Pxx1,f]=pmtm(y,4,Nfft,Fs); %用多窗口法(NW=4)估计功率谱
figure;subplot(2,1,1),plot(f,10*log10(Pxx1)); %绘制功率谱
xlabel('频率/Hz');ylabel('功率谱/dB');
title('多窗口法(MTM) nw=2原始信号功率谱');grid on
[Pxx,f]=pmtm(y,2,Nfft,Fs); %用多窗口法(NW=2)估计功率谱
subplot(2,1,2),plot(f,10*log10(Pxx)); %绘制功率谱
xlabel('频率/Hz');ylabel('功率谱/dB');axis([0 4000 -80 -20])
title('多窗口法(MTM) nw=2滤波后的信号功率谱');grid on
——摘自https://blog.csdn.net/MrShuang123/article/details/102622901
https://blog.csdn.net/Guinan_Li/article/details/78535311
https://blog.csdn.net/chenxingp123/article/details/24238509
https://blog.csdn.net/chenxingp123/article/details/24238657
https://blog.csdn.net/cqfdcw/article/details/84952301
浙公网安备 33010602011771号