熵、相对熵与互信息
熵
定义:一个离散型随机变量 \(X\) 的熵 \(H(X)\) 定义为:
\[H(X)=-\sum_{x \in X}p(x) \log p(x)
\]
注释:\(X\) 的熵又可以理解为随机变量 \(\log \frac{1}{p(X)}\) 的期望值
引理
- \(H(X) \geq 0\)
- \(H_b(X)=(\log_ba)H_a(X)\)
二元熵:
\[H(X)= -p\log p-(1-p)\log (1-p) \rightarrow H(p)
\]
\(H(p)\) 为上凸函数,在 \(p= \frac{1}{2}\) 时取得最大值 1

联合熵与条件熵
定义:对于服从联合分布为 \(p(x,y)\) 的一对离散随机变量 \((x,y)\) ,其联合熵 \(H(X,Y)\) 定义为:
\[\begin{align}
H(X,Y)=&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x,y)\\
=&-E \log p(X,Y)
\end{align}
\]
定义:条件熵 \(H(Y|X)\) 定义为:
\[\begin{aligned}
H(Y|X)=&\sum_{x \in X}p(x)H(Y|X=x)\\
=&-\sum_{x \in X}p(x)\sum_{y \in Y}p(y|x)\log p(y|x)\\
=&-\sum_{x \in X} \sum_{y \in Y}p(x,y)\log p(y|x)\\
=&-E \log p(Y|X)
\end{aligned}
\]
定理:链式法则
\[H(X,Y)=H(X)+H(Y|X)
\]
证明:
\[\begin{align}
H(X,Y)=&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x,y)\\
=&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x) p(y|x)\\
=&-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(x) -\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(y|x)\\
=&-\sum_{x \in X}p(x) \log p(x)-\sum_{x\in X} \sum_{y \in Y}p(x,y)\log p(y|x)\\
=&H(X)-H(Y|X)
\end{align}
\]
等价于:
\[\log p(X,Y)=\log p(X)+\log p(Y|X)
\]
推论:
\[H(X,Y|Z)=H(X|Z)+H(Y|X,Z)
\]
相对熵和互信息
相对熵(relative entropy) 是两个随机分布之间距离的度量。相对熵 \(D(p||q)\) 度量当真实分布为 \(p\) 而假定分布为 \(q\) 时的无效性。
定义:两个概率密度函数为 \(p(x)\) 和 \(q(x)\) 之间的相对熵或 \(\text{Kullback-Leibler}\) 距离定义为
\[\begin{align}
D(p||q)=&\sum_{x \in X}p(x)\log \frac{p(x)}{q(x)}\\
=&E_p \log \frac{p(x)}{q(x)}
\end{align}
\]
互信息(mutual information) 是一个随机变量包含另一个随机变量信息量的度量。互信息也是给定另一个随机变量知识的条件下,原随机变量不确定度的缩减量。
定义:考虑两个随机变量 \(X\) 和 \(Y\),它们的联合概率密度函数为 \(p(x,y)\),其边际概率密度函数为 \(p(x)\) 和 \(p(y)\)。互信息 \(I(X;Y)\) 为联合概率分布 \(p(x,y)\) 和乘积分布 \(p(x)p(y)\) 之间的相对熵
\[\begin{align}
I(X;Y)=&\sum_{x \in X,y \in Y}p(x,y) \log \frac{p(x,y)}{p(x)p(y)}\\
=& D(p(x,y)||p(x)p(y))
\end{align}
\]
注:一般情况下 \(D(p||q) \neq D(q||p)\)
熵和互信息的关系
互信息 \(I(X;Y)\) 可重写为:
\[\begin{align}
I(X;Y)=&\sum_{x \in X,y \in Y}p(x,y) \log \frac{p(x,y)}{p(x)p(y)}\\
=& \sum_{x \in X,y \in Y}p(x,y) \log \frac{p(x|y)}{p(x)}\\
=& \sum_{x \in X,y \in Y}p(x,y) \log p(x|y)-\sum_{x \in X,y \in Y}p(x,y) \log p(x)\\
=& \sum_{x \in X,y \in Y}p(x,y) \log p(x|y)-\sum_{x \in X}p(x) \log p(x)\\
=& H(X)-H(X|Y)
\end{align}
\]
由此可表明互信息 \(I(X;Y)\) 是给定 \(Y\) 的情况下 \(X\) 的不确定度的缩减量。
由对称性,可得:
\[I(X;Y)=H(Y)-H(Y|X)
\]
由 \(H(X,Y)=H(X)+H(Y|X)\) 可得:
\[I(X;Y)=H(X)+H(Y)-H(X,Y)
\]
最后注意到:
\[I(X;X)=H(X)-H(X|X)=H(X)
\]
因此,随机变量和自身的互信息为该随机变量的熵,因此将熵称为自信息(self-information)
定理:互信息与熵的关系
\[\begin{align}
I(X;Y)=&H(X)-H(X|Y)\\
I(X;Y)=&H(Y)-H(Y|X)\\
I(X;Y)=&H(X)+H(Y)-H(X;Y)\\
I(X;Y)=&I(Y;X)\\
I(X;X)=&H(X)\\
\end{align}
\]
Venn 图:互信息和熵的关系可由文氏图给出
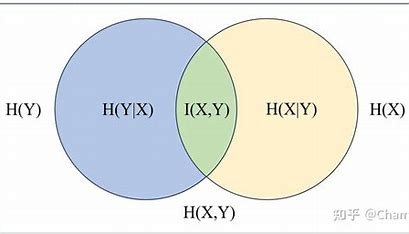
熵、相对熵与互信息的链式法则
定理(熵的链式法则):
\[H(X_1,X_2, \cdots ,X_n)=\sum_{i=1}^{n}H(X_i|X_{i-1},\cdots,X_1)
\]
证明:
\[\begin{align}
H(X_1,X_2)=&H(X_1)+H(X_2|X_1)\\
H(X_1,X_2,X_3)=&H(X_1)+H(X_2,X_3|X_1)\\
=&H(X_1)+H(X_2|X_1)+H(X_3|X_2,X_1)\\
\cdots\\
H(X_1,X_2, \cdots ,X_n)=&\sum_{i=1}^{n}H(X_i|X_{i-1},\cdots,X_1)
\end{align}
\]
定义(条件互信息):随机变量 \(X\) 和 \(Y\) 在给定随机变量 \(Z\) 时的条件互信息定义为
\[\begin{align}
I(X;Y|Z)=&H(X|Z)-H(X|Y,Z)\\
=&E_{p(x,y,z)} \log \frac{p(X,Y|Z)}{p(X|Z)p(Y|Z)}
\end{align}
\]
定理(互信息的链式法则):
\[I(X_1,X_2,\cdots ,X_n;Y)=\sum^n_{i=1}I(X_i;Y|X_{i-1},X_{i-2},\cdots ,X_1)
\]
证明:
\[\begin{align}
I(X_1,X_2,\cdots ,X_n;Y)=&H(X_1,X_2,\cdots ,X_n)-H(X_1,X_2,\cdots ,X_n|Y)\\
=& \sum_{i=1}^n H(X_i|X_{i-1},\cdots,X_1)-\sum_{i=1}^n H(X_i|X_{i-1},\cdots,X_1,Y)\\
=& \sum_{i=1}^n I(X_i;Y|X_{i-1},\cdots,X_1)
\end{align}
\]
Jensen 不等式及其结果
定义(下凸函数):若对于任意的 \(x_1,x_2 \in (a.b)\) 及 \(0 \leq \lambda \leq 1\),满足
\[f(\lambda x_1+(1-\lambda)x_2) \leq \lambda f(x_1)+(1-\lambda)f(x_2)
\]
则称函数 \(f(x)\) 在区间 \((a,b)\) 上是严格下凸的。
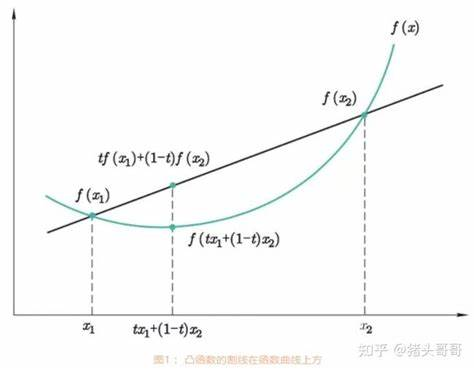
定理:如果函数 \(f\) 在某个区间存在非负的二阶导数,则 \(f\) 为该区间的凸函数。
定理(Jessen 不等式):若给定一个下凸函数 \(f\) 和一个随机变量 \(X\) ,则
\[Ef(X)\geq f(EX)
\]
证明:利用数学归纳法进行证明,对于一个两点分布,我们有
\[p_1f(x_1)+p_2f(x_2)\geq f(p_1x_1+p_2x_2)
\]
设分布点个数为 \(k-1\) 的时候定理成立,此时记 \(p_i'=\frac{p_i}{1-p_k}(i=1,2,\dots k-1)\),则有
\[\begin{align}
\sum_{i=1}^k p_if(x_1) =& p_kf(x_k)+(1-p_k)\sum_{i=1}^{k-1}p_i'f(x_i)\\
\geq & p_kf(x_k)+(1-p_k)f(\sum_{i=1}^{k-1}p_i'x_i)\\
\geq & f(p_kx_k+(1-p_k)\sum_{i=1}^{k-1}p_i'x_i)\\
\geq & f(\sum_{i=1}^k p_ix_i)
\end{align}
\]
定理(信息不等式):设 \(p(x)\),\(q(x)\) 为两个概率密度函数,则
\[D(p(x)||q(x)) \geq 0
\]
当且仅当对任意的 \(x\) ,\(p(x)=q(x)\) 时等号成立。
证明:
\[\begin{align}
-D(p||q)=&-\sum_{x \in X}p(x)\log \frac{p(x)}{q(x)}\\
=&\sum_{x \in X}p(x)\log \frac{q(x)}{p(x)}\\
\leq & \log \sum_{x \in X} p(x)\frac{q(x)}{p(x)}\\
=& \log \sum_{x \in X} q(x)\\
=& \log 1\\
=& 0
\end{align}
\]
当且仅当 \(\frac{q(x)}{p(x)}=c\) 时等号成立,\(\sum_{x \in X}c p(x)=1 \rightarrow c=1 \rightarrow p(x)=q(x)\)
推论(互信息的非负性):对于任意两个随机变量 \(X\),\(Y\),
\[I(X;Y) \geq 0
\]
证明:\(I(X;Y)=D(p(x,y)||p(x)p(y)) \geq 0\),当且仅当 \(p(x,y)=p(x)p(y)\) ,即 \(X\) 和 \(Y\) 相互独立时取等号。
定理:\(H(X) \leq \log |\chi|\),其中 \(\chi\) 为 \(X\) 的字母表 \(\chi\) 的元素个数,当且仅当 \(X\) 服从 \(\chi\) 上的均匀分布时,等号成立。
证明:设 \(u(x)=\frac{1}{|\chi|}\) ,\(p(x)\) 是随机变量 \(X\) 的概率密度函数,有
\[D(p||u)=\sum p(x)\log \frac{p(x)}{u(x)}= \log |\chi | -H(X) \geq 0
\]
定理(条件作用使熵减小):
\[H(X|Y) \leq H(X)
\]
当 \(X\) 和 \(Y\) 相互独立时,等号成立。
定理(熵的独立界):
\[H(X_1,X_2, \cdots ,X_n) \leq \sum_{i=1}^n H(X_i)
\]
当且仅当 \(X_i\) 相互独立时等号成立。
证明:根据熵的链式法则
\[\begin{align}
H(X_1,X_2, \cdots ,X_n) = & \sum_{i=1}^n H(X_i|X_{i-1},\cdots,X_1)\\
\leq & \sum_{i=1}^n H(X_i)
\end{align}
\]






 浙公网安备 33010602011771号
浙公网安备 33010602011771号