Label-constrained shortest path query processing on road networks

写在前边：花了太多时间来研究一些细枝末节的东西，感觉有点走远了，之后的文章主要研究：

1.这个文章提出的是什么问题

2.喷了之前的什么方法不太行

3.文章提出的方法的主要创新点在哪里

这篇文章主要解决的问题是：路径带标签的两点之间最短路，大概就是每条路径会给一个标签，然后你走的时候，只能走在标签集合内的路径，在这种情况下求两点之间最短路

一种朴素的做法是，假如我们考虑没有标签的两点之间最短路问题，可以用图的树分解，将图分解成一棵树，树上每一个节点是图上一组点的集合，比如说树节点X(1)={2,3,4}，在这个树节点中，包含图上1，2，3，4节点的信息，也包含1到2，3，4的最短路。根据树分解的性质，对于每组查询（u，v），可以查询u，v到LCA节点的最短路，找到其中最短的一条路径即为答案。

然后对于有标签的图，最朴素的做法就是对每一种标签集合做一次图的树分解，然后再对应的标签集合上直接查找就行了。如果内存没那么多，不能支持储存这么多集合的话，就用LRU算法来实现循环删除。但是这个算法的缺陷在于，如果每次用到的树分解都不在LRU储存的范围之内，每次都要跑一个Dijkstra，那还不如直接做一个单源最短路

文章提出的的算法是：事实上，有很多标签集合包含的最短路长度是相同的，意味着有很多的重复信息，对于这些重复信息，文章提出对它们进行压缩，这样能大大降低储存的空间复杂度

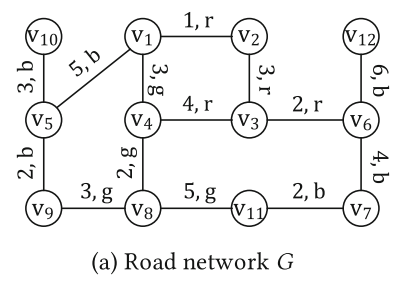
比如说这么一个图，对某个标签集合建图：

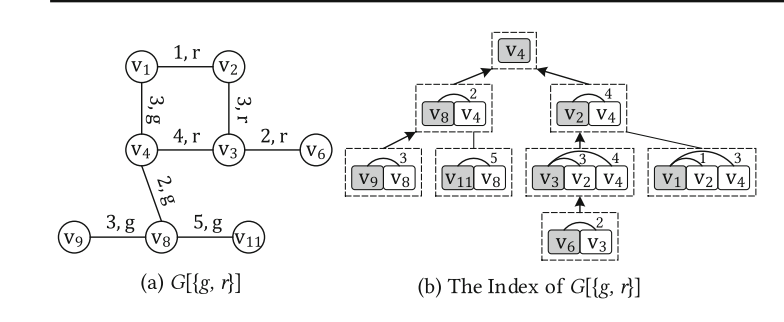
如果压缩法建图：

 

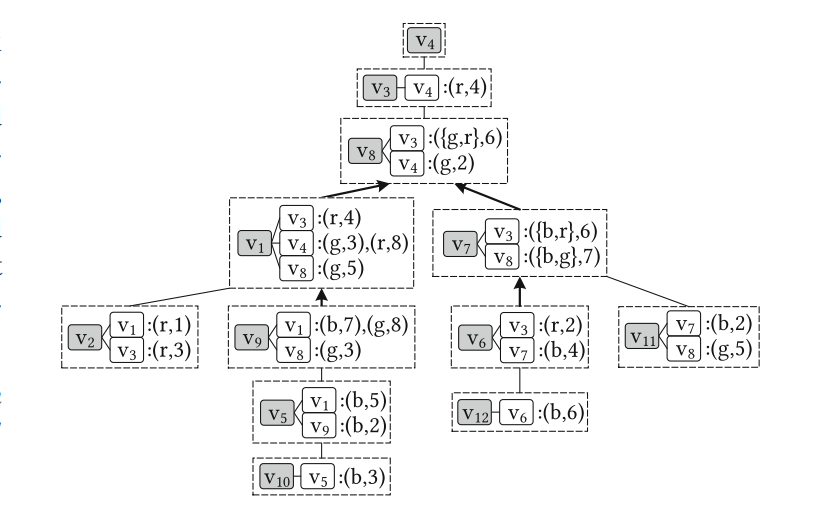
把所有的信息都压缩进来了