【线性代数的本质】 —— 学习笔记

【线性代数的本质】

原视频请移步至☞：【熟肉】线性代数的本质——3Blue1Brown

01-向量究竟是什么

• 向量是空间中的箭头
  首先确定一种思考向量的特定方式：
  因为目前所关注的主要是几何方面，所以每当引入一个关于向量的新主题的时候，需要首先想出一个落在某个坐标系中的箭头，例如在\(x-y\)平面中，并且箭头起点在原点。
• 向量是有序的数字列表
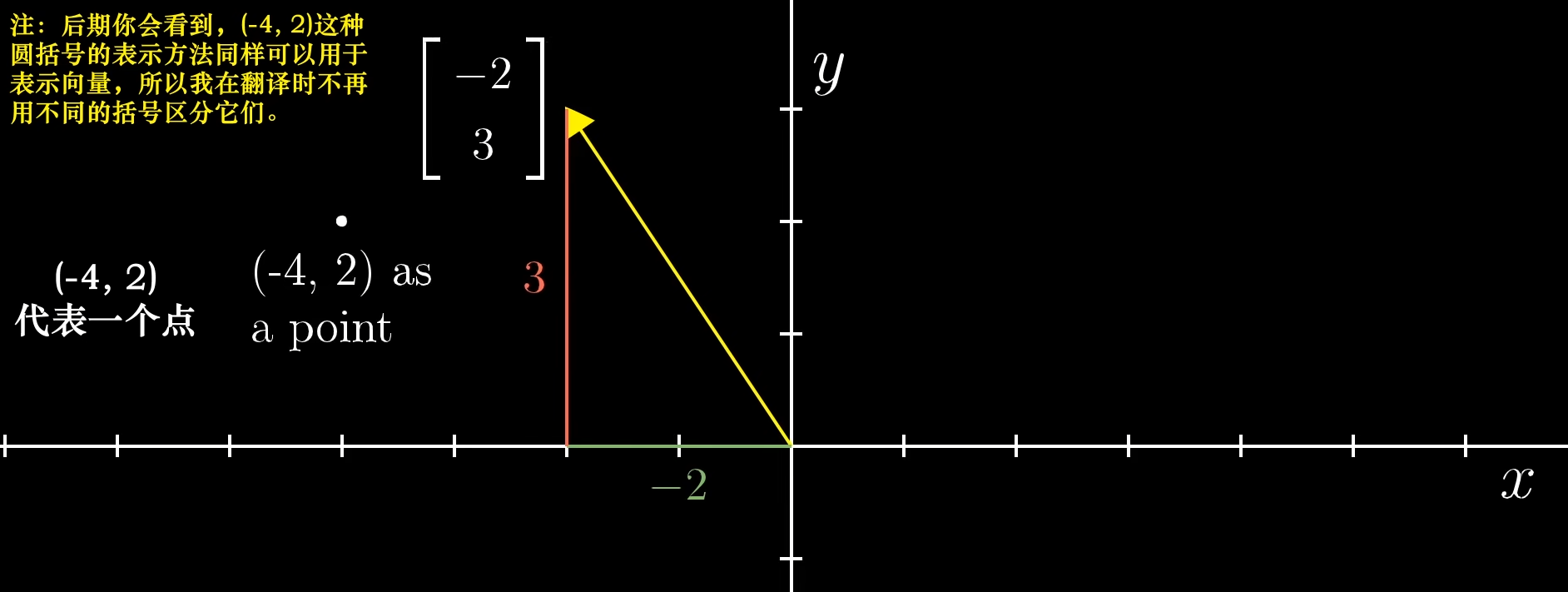
  可以通过向量坐标来理解：\(\begin{bmatrix}-2 \\ 3\end{bmatrix}\)、\(\begin{bmatrix}1 \\ 2\end{bmatrix}\)。

二维空间来看

一个向量的坐标由一对数构成，这对数指导你如何从原点（向量起始）出发到达尖端（向量终点）。每一对数对应唯一一个向量，每一个向量对应唯一一对数。

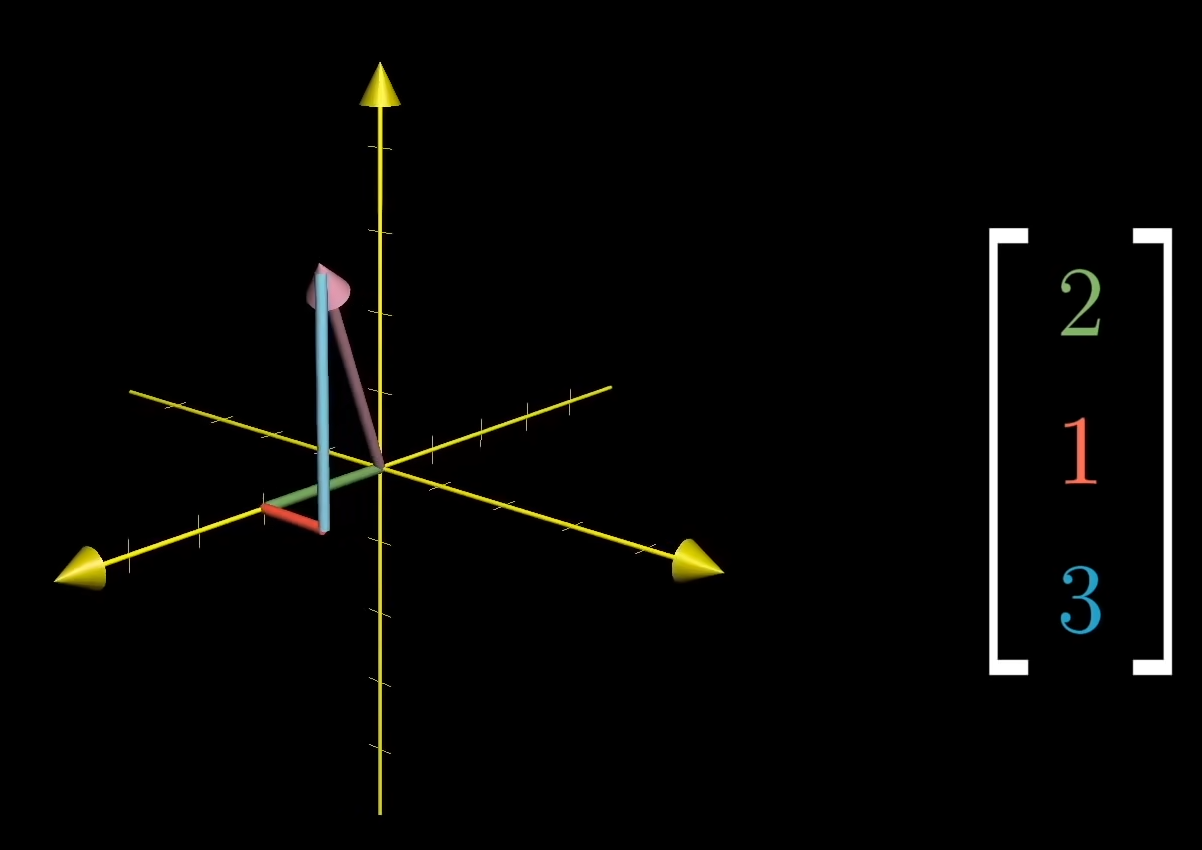
三维空间来看

多加一个\(z\)轴后，目前每一个向量都对应一个有序的三元数组。每一个三元数组对应唯一一个向量，每一个向量对应唯一一个三元数组。

向量加法

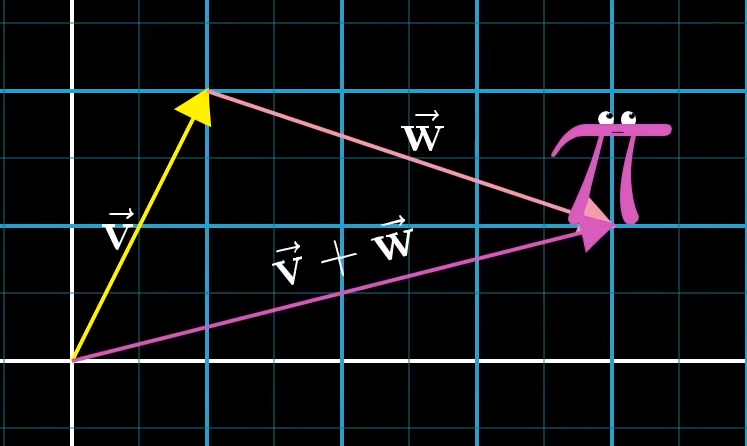
空间角度

向量加法差不多是线性代数中唯一允许向量离开原点的情形。
这里可以把向量看作空间中的一种特定的运动，即在空间中朝着某一个向量迈出一定距离☞。

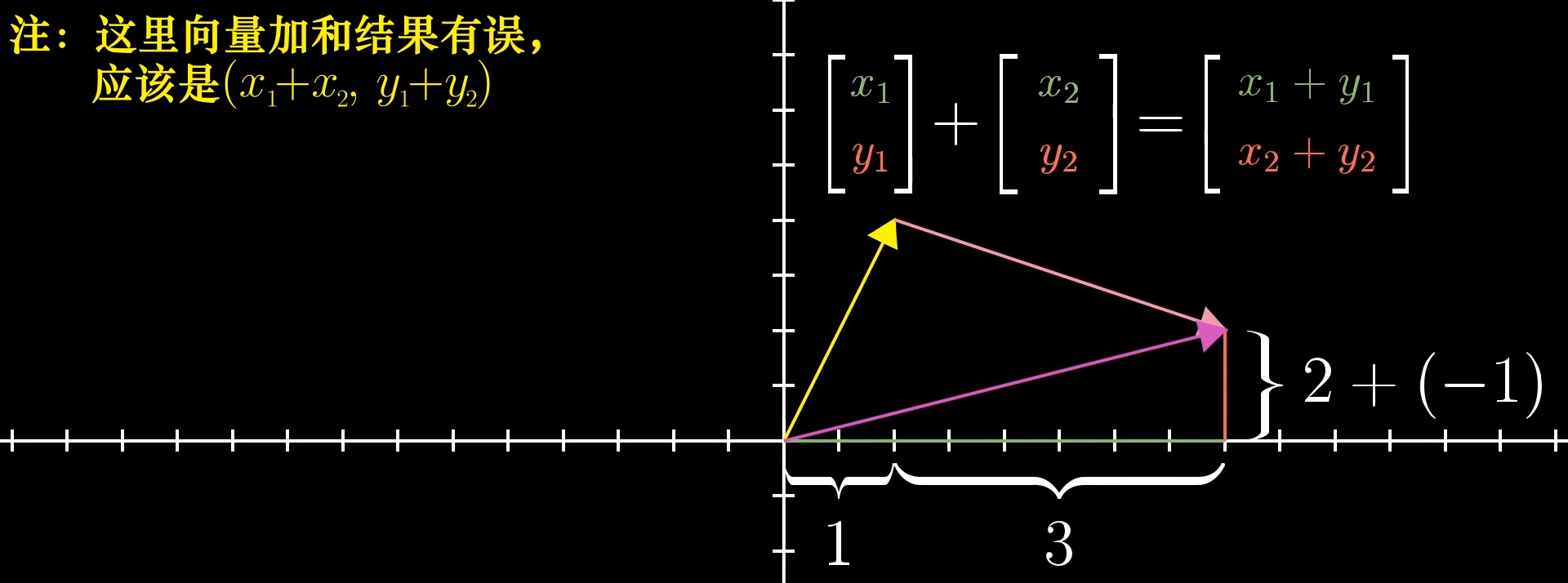
数字角度

当使用向量首尾连接的方法加和向量时，可以将其看作从原点出发，到第二个向量终点的四步运动：向右1步，向上2步，向右3步，最后向下1步。
在向量是有序列表的观点里，向量加法就是把对应项相加。

向量数乘

向量乘以一个标量，对向量进行拉伸或压缩，有时又使向量反向的过程被称为“缩放”。
而我们选择的：\(2,\frac{1}{3},-1.8...\)或其他的任何数，其用于缩放向量，被称为标量。自始至终，数字在线性代数中起到的主要作用就是缩放向量，故“标量”与“数字”其实可以相互替换。

数字/几何角度

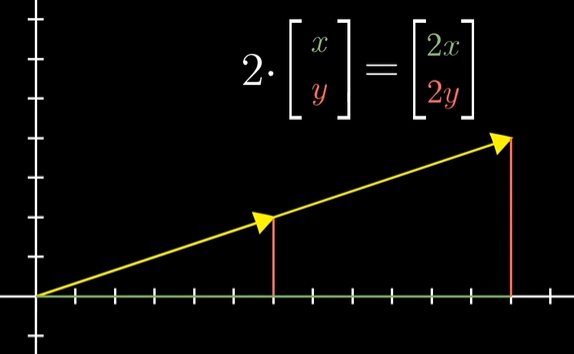
将一个向量伸长为原来的两倍，对应于将每一个向量分别乘以2。
所以将向量看作一个数字列表的时候，向量与标量相乘就是将向量中的每一个分量与标量相乘。

01-总结

实际上无论怎么看待向量都无所谓，或者把向量看作空间中的箭头，把向量看作数字列表，有几何意义与之对应；或者数字列表看作向量，有数值表示与之对应。线性代数更多体现的就是能够在这两种观点（几何、数字）之间相互转化。

02-线性组合.张成的空间与基