题解：CF2176D Fibonacci Paths

前言

想用这道题作为我引入一类“用边做状态的图上 dp（线图上 dp）”的题目的一次契机。

简要题意

洛谷上的题面已经挺简要了：CF2176D Fibonacci Paths，同时沿用其变量名与记号。

分析

做一些让我深刻的题时，我会将它们归类到一些题单中。这道题被我丢到了“用边做状态的图上 dp（线图上 dp）”合集。

在开始着手解决这道题之前，可以先想一个问题，为什么要拿边当状态？换句话说，是为了解决什么困难？

大多数题和这道题一样——因为边携带着两个端点的信息。有时我们不仅想知道当前在什么结点，还想知道我们是从哪个结点来的，于是会自然地想到用边的编号来当 dp 的状态之一。

可以再想一个问题，在用边当状态的题目中，大概率会迎来哪些挑战？换句话说，不带任何观察，直接用边做状态下手解决，困难在哪里？也就是这道题的优化方向。

大多数题也和这道题一样。我接下来将用边当状态和用点当状态进行对比来分析。

用点作为状态时，若保证每个点只被访问 \(\Theta(1)\) 次，每次的操作是遍历出边的话，那么总复杂度是 \(\Theta(n + m)\) 的，这是因为 \(\sum_{i=1}^n \text{deg}_i = \Theta(m)\)。

但若只保证每条边被访问 \(\Theta(1)\) 次，每次的操作是遍历任意一个端点的出边的话，那么总复杂度是 \(O(m^2)\) 的。

\(n\) 与 \(m\) 同阶时，一个极端的构造：

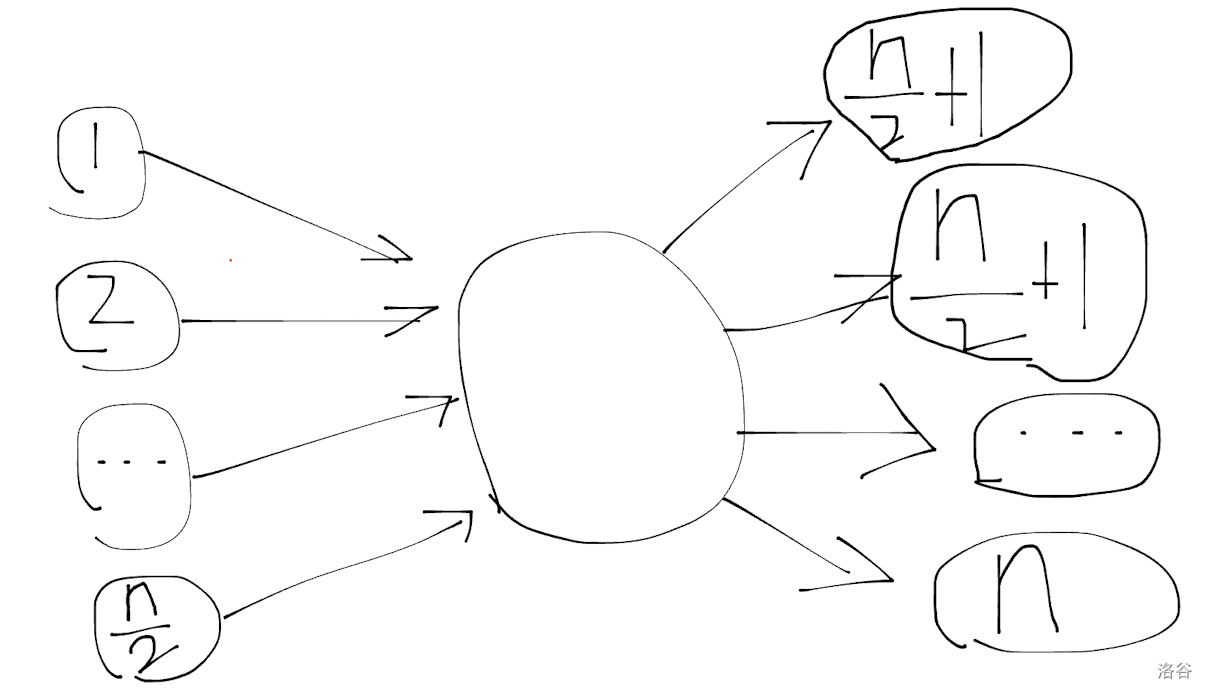
因此我们需要优化转移，不能对于每条边都遍历出边。这通常是我们做这类题的目标。

思路

朴素 —— \(O(m^2)\)

思路

先设计朴素 dp 再在其基础上优化。

设 \(S_i\) 为所有始发边是 \(i\) 这条边，合法的简单路径组成的集合，\(f_i\) 为 \(|S_i|\)。

这自然是个不交的等价类划分，因此最终答案即为 \(\sum_{i=1}^m f_i\)。

\(f_i\) 的转移可以划分成两类不交的等价类：

• 第一类：没有后续边

  即简单路径只有 \(i\) 这一条边，这部分贡献是 \(1\)

• 第二类：有后续边

  设第 \(i\) 条边的两个端点分别为 \(u_i, v_i\)，其中 \(u_i \to v_i\)。那么如果 \(i\) 的后续边要想是 \(j\)，一定要满足 \(v_i = u_j\) 且 \(a_{u_i} + a_{v_i(u_j)} = a_{v_j}\)。

  对于 \(S_j\) 中的每一条简单路径，按照定义，始发边一定是 \(v_i(u_j) \to v_j\)；将其替换为 \(u_i \to v_i(u_j) \to v_j\) 后，一定仍合法，且起始边为 \(u_i \to v_i\)，完美符合定义；因此 \(\forall \, x \in S_j\) 经过如此替换后一定有 \(x \in S_i\)。

  从而这一部分的贡献是所有符合要求的边 \(j\) 的 \(f_j\) 的和。

按照以上分讨，可以列出如下的状态转移公式：

\[f_i = 1 + \sum_{j = 1}^m [v_i = u_j] \cdot [a_{u_i} + a_{v_i} = a_{v_j}] \cdot f_j \]

发现是有自然的拓扑序的。因为保证 \(a_{i} \ge 1\) 时若有 \(a_{u_i} + a_{v_i} = a_{v_j}\)，则有 \(a_{u_i} = a_{v_j} - a_{v_i} \leq a_{v_j} - 1\)，即一条简单路径上的 \(a_{u_{i}}\) 单调上升是必要的。

直接记忆化搜索好了。

实现

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

constexpr int N = 200000 + 1, P = 998244353;

ll a[N];
int u[N], v[N], f[N];
vector<int> adj[N];

void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        adj[i].clear();
    }
    for (int i = 1; i <= m; ++i) {
        cin >> u[i] >> v[i];
        adj[u[i]].push_back(i);
        f[i] = -1;
    }
    auto dfs = [](auto &&self, int e) {
        if (f[e] != -1) {
            return ;
        }
        int u = ::u[e], v = ::v[e];
        ll res = 1;
        for (int i : adj[v]) if (a[u] + a[v] == a[::v[i]]) {
            self(self, i);
            res += f[i];
        }
        f[e] = res % P;
    };
    ll ans = 0;
    for (int i = 1; i <= m; ++i) {
        dfs(dfs, i);
        ans += f[i];
    }
    cout << ans % P << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

事实上，用邻接表存图的复杂度和直接遍历所有边的最坏复杂度是一样的，一个是 \(O(m^2)\) 一个是 \(\Theta(m^2)\)。

优化 —— \(\Theta(n + m)\)

这次先看实现再看思路。

实现

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

constexpr int N = 200000 + 1, P = 998244353;

ll a[N];
int u[N], v[N], f[N];
map<ll, vector<int>> adj[N];
map<ll, int> g[N];

void solve() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        adj[i].clear();
        g[i].clear();
    }
    for (int i = 1; i <= m; ++i) {
        cin >> u[i] >> v[i];
        adj[u[i]][a[v[i]]].push_back(i);
        f[i] = -1;
    }
    auto redu = [](const auto& x) {
        return x >= P ? x - P : x;
    };
    auto dfs = [&](auto &&self, int e) {
        if (f[e] != -1) {
            return ;
        }
        int u = ::u[e], v = ::v[e];
        ll tar = a[u] + a[v];
        auto res = g[v].emplace(tar, 0);
        if (res.second) {
            ll sum = 0;
            if (auto itr = adj[v].find(tar); itr != adj[v].end()) {
                for (int i : itr->second) {
                    self(self, i);
                    sum += f[i];
                }
            }
            res.first->second = sum % P;
        }
        f[e] = redu(res.first->second + 1);
    };
    ll ans = 0;
    for (int i = 1; i <= m; ++i) {
        dfs(dfs, i);
        ans += f[i];
    }
    cout << ans % P << '\n';
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

时间复杂度 \(O(m \log m)\)。

思路

观察 \(O(m^2)\) 实现的 dfs 体内：

auto dfs = [](auto &&self, int e) {
    if (f[e] != -1) {
        return ;
    }
    int u = ::u[e], v = ::v[e];
    ll res = 1;
    for (int i : adj[v]) if (a[u] + a[v] == a[::v[i]]) {
        self(self, i);
        res += f[i];
    }
    f[e] = res % P;
};

试着做一些不改变形式的等价变换。可以注意到：

• “只遍历‘有用边’”：\(v\) 的出边中，只有那些另一个端点 \(w\) 满足 \(a_u + a_v = a_w\) 的边（“有用边”）会对 res 有贡献。

  因此每次可以只遍历“有用边”。可以使用 map 提前将一个点的出边中，满足另一个端点 \(w\) 的 \(a_w\) 是一个定值 \(x\) 的边筛出（代码中， adj[u][x] 即为这样的边组成的集合。下文称其为 \(u\) 的目标 \(x\) 集合（这样的集合有可能是空的））。

• “记忆化”：对于相同的 \((v, a_u + a_v)\)，做的事情总是一样的。

  所以 \(\text{res}\) 也总是相同的。可以使用 map 进行“记忆化”。

事实上，做了这两个优化后，就会有：

• “记忆化”带来的保证：对于每个结点 \(v\)，相同的 \(a_u + a_v\) 只会导致遍历 \(v\) 的目标 \(a_u + a_v\) 集合恰好一次。
• “只遍历有用边”带来的保证：划分是不交的，即原图上的每条边都会被划分到恰好其中一个结点 \(u\) 的恰好其中一个目标 \(x\) 集合。

因此每条边最多被 dfs 遍历一次，时间复杂度得证。

如果不是 Codeforces，没有必要使用 map。使用哈希表可以取到期望的最低时间复杂度：\(\Theta(n + m)\)。

总结

线图 dp 模型一般适用于需要同时知道当前结点与当前结点前驱的信息的情况。当然，若状态的依赖关系不是个 dag，即转移带环，也可以去 bfs，dijkstra，spfa 等。

时间复杂度的瓶颈一般在转移时的遍历所有出边上。尝试“记忆化”后“只遍历有用边”等方法优化遍历出边的复杂度，有时甚至没必要去遍历相同的出边集合超过常数次。

习题

[ABC414F] Jump Traveling 的官方题解做法，这里不过多赘述。