USACO23FEB-Gold/洛谷P9127 Equal Sum Subarrays
涉及知识点:贪心,递推(?
写在前面
-
这题虽然是一道黄题(其实应该评绿的),但这是对于 \(O(n^3)\) 的做法而言;这篇博客的做法是 \(O(n^2\log n)\),个人觉得大概算蓝。
-
这个做法细节很多,我七七八八算下来交了十几发才过,思路和另一个大佬有些像,但是相对于他的博客进行了一些优化,并且更详细地解释了这种 \(O(n^2\log n)\) 的做法。
题意
给你一个数组 \(a\),初始时数组的所有区间的区间和互不相同,对于每个 \(i\in [1,N]\),将 \(a_i\) 改为 \(a_i'\) 使得数组会有两个区间的区间和相等,求 \(\lvert a_i-a_i'\rvert\) 的最小值。
性质
-
我们很容易想到一个性质:称我们修改的数叫 \(i\),最后区间和相等的两个区间一定是一个区间包含 \(i\),一个不包含。原因很简单,因为对 \(i\) 修改过后包含 \(i\) 的所有区间的区间和都会变化 \(\Delta i\),假设两个区间都包含,那么他们这两个区间的相对大小和修改前一样,而修改前题目保证了没有任何区间和相等,因此同时包含 \(i\) 的两个区间修改后不可能区间和相等。
-
由于题目只让我们输出修改的最小差值,而不用输出具体方案,我们找到一个性质:两个区间有交的情况一定能归纳为无交的情况。
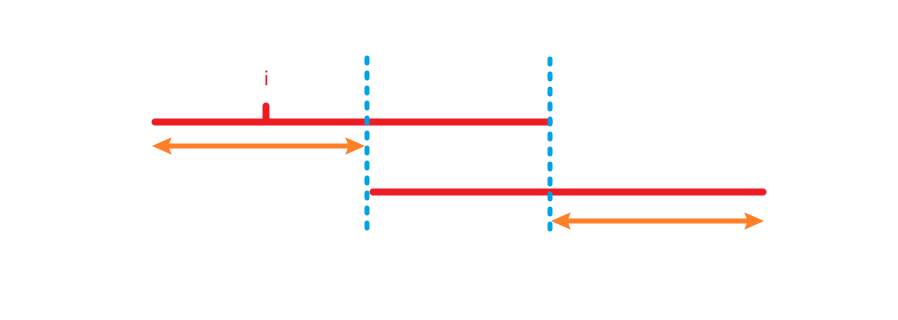
(1). 考虑两个区间交叉的情况
如图,由于我们修改的 \(i\) 由于上述性质不能同时被两个区间包含,那么对于修改后区间和相等的两个红色区间,我们同时减去蓝色虚线括起来的中间部分,就能归纳为两个无交的橙色区间修改后的区间和相等。
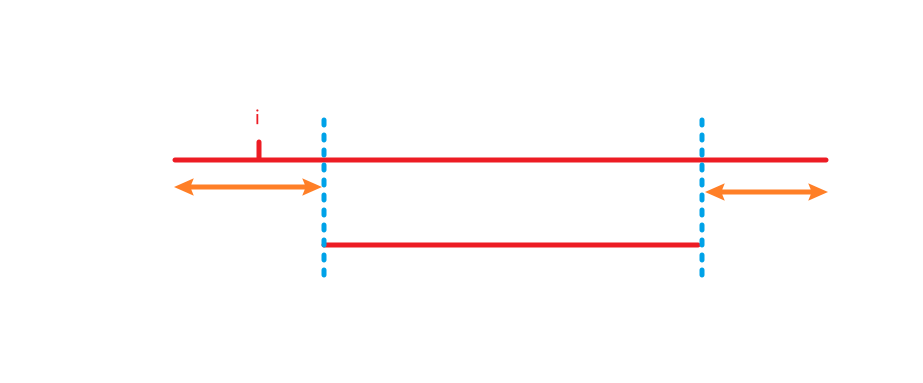
(2). 考虑一个区间包含另一个区间的情况
如图,对于这两个红色区间,可以归纳为两个橙色区间修改后的区间和互为相反数。
-
两个区间的区间和互为相反数的注意事项 (注意这里的“区间”概念同样也指一个数,即区间 \([i,i]\)):如果两个区间,修改后区间和相加为 \(0\),它们要对答案产生贡献仅当这两个区间中间还有其他数,或者这两个区间旁边还有其他数。
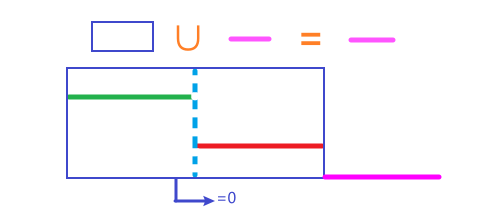
很显然,如果这两个区间中间有其他数则可归纳为性质二的区间包含的情况;而如果这两个区间是挨在一起的(如下图,红色和绿色代表这两个区间,粉色代表其他数),那么这两个区间可以合并为一个区间和为 \(0\) 的区间,加上旁边的数(粉色)就等于这个旁边的数,符合题目要求;而如果没有旁边的数,换句话说就是这两个区间已经占完了整个序列,这时候这两个区间的区间和等于 \(0\) 就没用了。
概括一下就是:要使得这两个区间的并集的补集非空。
做法
掌握了以上几个性质,我们总结一下最终我们需要干些什么:
找出两个不相交的区间,一个包含 \(i\),一个不含。要么使得 \(i\) 修改后两个区间的区间和相等,要么使得修改后两个区间的区间和互为相反数并且满足性质 3
我们枚举 \(l\) 作为分界点,将 \(l\) 之前(不包括 \(l\))的所有区间都放入一个 set 里面,再枚举 \(r\in [l,n]\),相当于枚举了所有以 \(l\) 开头的区间。此时有两种区间,一种是 \(l\) 左边的区间,一种是右边的区间 \([l,r]\)。我们用前缀和 \(O(1)\) 算出右边区间的区间和,再在 set 中 \(O(\log n)\) 二分找出与它区间和最接近的区间,求出它们区间和的差值,这个差值意味着:“\([l,r]\) 的区间和要等于另一个区间的区间和的最小差值”,注意这个“差值”可以应用于 \([l,r]\) 当中的任意一个数,因为 \([l,r]\) 中的任意一个数加上这个差值都可以使得 \([l,r]\) 的区间和等于另一个区间的区间和,所以所有 \(ans_i\ (i\in [l,r])\) 都要被这个差值更新一次。
但我们没有必要因此写数据结构维护 \(ans_i\) 的最小值,容易发现当 \(l\) 固定的时候,\(ans_i\) 会被 \([l,n],[l,n-1],\dots,[l,i]\) 更新一遍,所以我们只需要倒序枚举 \(r\) 即可。
举例:
\(ans_n\) 只会被 \([l,n]\) 更新
\(ans_{n-1}\) 会被 \([l,n],[l,n-1]\) 更新
\(ans_{n-2}\) 会被 \([l,n],[l,n-1],[l,n-2]\) 更新
\(\cdots\)
我们只需要倒序枚举 \(r=n\rightarrow l\),维护一个后缀 \(\min\) 即可
同理,前面我们找了区间和差值最小的两个区间,我们将 \([l,r]\) 的区间和取相反数,即可找区间和加起来等于 \(0\) 的最小修改代价。具体实现代码与上文相同,只是确定了两个区间后碍于性质 3 我们需要判断他们的并集是否覆盖了全部区间。
最后,需要注意一点,最开始的时候 \(ans_i\) 需要设为 \(num_i\),表示它把自己变为 \(0\) 的代价(题目似乎保证了 \(N\geq 2\),不用与担心性质 3 冲突)。
代码
最后放上代码,小提醒:由于涉及大量区间操作,for 的时候注意区间的范围、区间的开闭。
#include<bits/stdc++.h>
using namespace std;
template<class T>inline void rd(T &x){
T res=0,f=1;
char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1; ch=getchar();}
while(isdigit(ch)){res=res*10+ch-'0';ch=getchar();}
x=res*f;
}
template<class T>inline void wt(T x){
if(x<0){x=-x;putchar('-');}
if(x>9) wt(x/10);
putchar(x%10+'0');
}
typedef long long LL;
const LL LLINF=numeric_limits<LL>::max()-1;
const int MAXN=505;
int n;
struct Node{
LL val;
int l,r;
bool operator < (const Node &y) const{
return val<y.val;
}
};
LL a[MAXN],pre[MAXN],ans[MAXN];
set<Node>s;
inline bool is_range_merge_cover_all(int l1,int r1,int l2,int r2){
if(l1>l2) swap(l1,l2),swap(r1,r2);
// cout<<l1<<' '<<r1<<' '<<l2<<' '<<r2<<endl;
if(r1+1<l2) return false;
if(l1<=1 && max(r1,r2)>=n) return true;
return false;
}
int main(){
rd(n);
if(n==2){//特判n==2
rd(a[1]);rd(a[2]);
cout<<min(abs(a[1]),abs(a[2]-a[1]))<<endl<<min(abs(a[2]),abs(a[2]-a[1]));
return 0;
}
pre[0]=0;
for(int i=1;i<=n;i++){
rd(a[i]);
ans[i]=abs(a[i]);//将自己变为0的代价
pre[i]=pre[i-1]+a[i];
}
LL tmp,minx;
set<Node>::iterator res;
s.insert({a[1],1,1});
for(int l=2;l<=n;l++){
minx=LLINF;
for(int r=n;r>=l;r--){
tmp=pre[r]-pre[l-1];
minx=min(minx,abs(tmp));//这一步的原因是将这个数变为0过后任意相邻区间加它都等于自己
res=s.lower_bound({tmp,-1,-1});//找后继
if(res!=s.end()) minx=min(minx,abs(res->val-tmp));
if(res!=s.begin()){
res--;//找前驱
minx=min(minx,abs(res->val-tmp));
}
ans[r]=min(ans[r],minx);
tmp=-tmp;//找与这个区间和的相反数最接近的区间和,使他们抵消成为0的代价最小
res=s.lower_bound({tmp,-1,-1});//找后继
if(res!=s.end())
if(!is_range_merge_cover_all(l,r,res->l,res->r))
minx=min(minx,abs(res->val-tmp));//如果这两个区间覆盖了所有数则无法满足题目条件
if(res!=s.begin()){
res--;//找前驱
if(!is_range_merge_cover_all(l,r,res->l,res->r))
minx=min(minx,abs(res->val-tmp));
}
ans[r]=min(ans[r],minx);
}
for(int i=1;i<=l;i++)
s.insert({pre[l]-pre[i-1],i,l});
}
s.clear();
s.insert({a[n],n,n});
for(int r=n-1;r>=1;r--){
minx=LLINF;
for(int l=1;l<=r;l++){
tmp=pre[r]-pre[l-1];
minx=min(minx,abs(tmp));
res=s.lower_bound({tmp,-1,-1});//找后继
if(res!=s.end()) minx=min(minx,abs(res->val-tmp));
if(res!=s.begin()){
res--;//找前驱
minx=min(minx,abs(res->val-tmp));
}
ans[l]=min(ans[l],minx);
tmp=-tmp;
res=s.lower_bound({tmp,-1,-1});//找后继
if(is_range_merge_cover_all(l,r,res->l,res->r)) continue;
if(res!=s.end())
if(!is_range_merge_cover_all(l,r,res->l,res->r))
minx=min(minx,abs(res->val-tmp));
if(res!=s.begin()){
res--;//找前驱
if(!is_range_merge_cover_all(l,r,res->l,res->r))
minx=min(minx,abs(res->val-tmp));
}
ans[l]=min(ans[l],minx);
}
for(int i=n;i>=r;i--)
s.insert({pre[i]-pre[r-1],r,i});
}
for(int i=1;i<=n;i++) wt(ans[i]),putchar('\n');
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号