动态规划——背包问题（二）

昨天逛知乎，看见一个对完全背包时空复杂度优化的定量解法，觉得的非常好
于是，本篇博客，我将记录对01、完全背包中时间、空间复杂度优化的详解，作为昨天博客内容 动态规划——背包问题（一）01背包和完全背包 的补充

首先是题目

完全背包问题

从上一篇文章中我们先列出了最开始的完全背包状态转移方程：
f[i][j]=max(f[i-1][j],f[i-1][j-k*weight[i]]+k*value[i])，(k*weight[i]<=j)

而01背包则是：
f[i][j]=max(f[i-1][j],f[i-1][j-weight[i]]+value[i])

那么，完全背包就是01背包的扩展，区别就是：
对于01背包问题，k=0,1;
对于完全背包问题，k=0,1,2,3,...,j/weight[i]
只要对k的范围稍作改动，二者完全可以统一

完全背包问题的算法优化：

1.时间复杂度优化
首先，我们将状态转移方程展开得到如下k+1个式子：

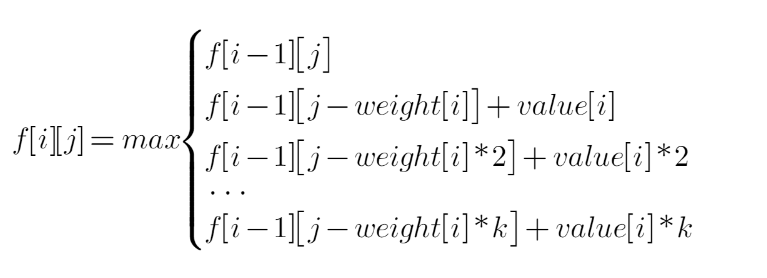
利用待定系数法，用j-weight[i]替换上式中的j得到：

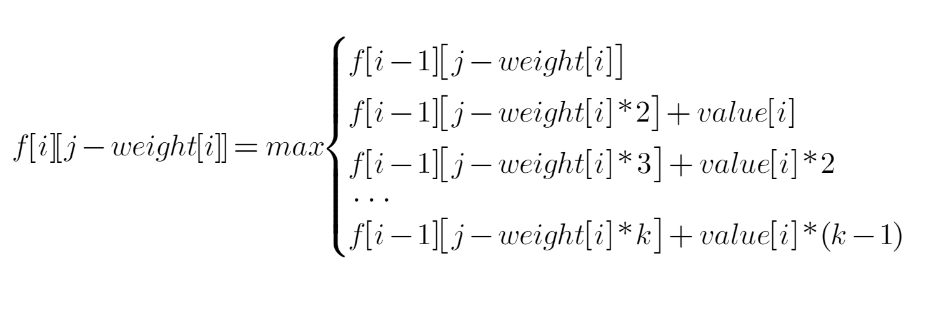
等式两边同时加上value[i]：

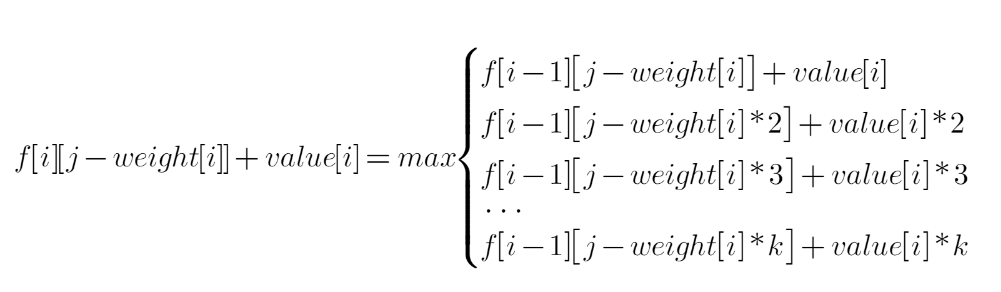
此时，我们发现，三式中的(1)...(k)和一式中的(2)...(k+1)式重合

所以，原状态转移方程可以简化为：
f[i][j]=max(f[i-1][j],f[i][j-weight[i]]+value[i])

这样就把原来均摊时间复杂度为O(m)的状态转移优化到了O(1)
对于第i件物品，面临两种选择；一个也不拿：f[i-1][j]和至少拿一个：f[i][j-weight[i]]+value[i]，其实f[i][j-weight[i]]+value[i]在一次又一次的遍历和比较之中已经通过不断的j-weight[i]实现了k*weight[i] ；又通过不断的+value[i]实现了+k*value[i]，再通过一轮轮的max()比较和覆盖，得出最后的值

2.空间复杂度优化

f[j]=max(f[j],f[j-weight[i]]+value[i])

可以看这张图：

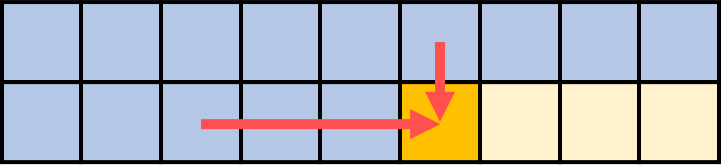
深黄色格子就是代表了f[i][j]，由于它取决于上面一行的f[i][j]和同一行的f[i][j-weight[i]]，因此在优化后的转移方程中，我们发现max()的左值f[j]即为原来处于上一行的f[i-1][j]，右值中的f[j-weight[i]]+value[i]即为原来处于同一行的f[i][j-weight[i]]+value[i]，因为每次得到的结果都是二者的最大值，因此覆盖后得到的新的f[j]完全可以保存当前的结果，参与下一轮循环

最后给出完全背包问题的代码：

#include<iostream>
using namespace std;
int N,M,weight[32]={0},value[32]={0},f[202]={0}; //N-物品种类数 M-背包的总容量 
int main()
{
	cin>>M>>N;
	for(int i=1;i<=N;i++) cin>>weight[i]>>value[i];
	for(int i=1;i<=N;i++){
		for(int j=0;j<=M;j++){
			if(weight[i]>j)
				continue;
			f[j]=max(f[j],f[j-weight[i]]+value[i]);
		}
	}
	cout<<"max="<<f[M];
	return 0;
}

---

本文完