后缀结构

1.后缀数组

引入

结构

后缀数组一般由两个数组组成：
\(sa_i\)，表示按照字典序排序第 \(i\) 小的是哪个后缀。
\(rk_i\)，表示第 \(i\) 个后缀排名第几。
有 \(sa_{rk_i}=rk_{sa_i}=i\)

计数排序

是一种支持排序算法，时间 \(O(n+V)\)。 \(V\) 为值域。
是稳定的。
我们设我们现在对 \(a\) 数组排序，要求稳定。
首先，我们先把每个 \(a\)，\(cnt_a\) 加 1。
然后，我们把 \(cnt\) 做一个前缀和。
最后，我们倒序枚举 \(i\)，令 \(A_{cnt_i}=a_i,cnt_i=cnt_i-1\)。
最后 \(A\) 即为答案。

如果我们对 \((a_i,b_i)\) 排序，其中 \(b_i\in[1,n]\)。
设一个数组 \(r_{b_i}=a_i\)，
那么我们只需把最后一步换成，倒序枚举 \(r_i\) 即可。

运用倍增计算

我们假设已知 \(i\) 开头的长 \(2^k\) 的后缀的 \(sa,rk\) 数组。
那么我们是否也能求出 \(2^{k+1}\) 长度的呢？
很简单，我们以 \(rk_i\) 为第一关键字， \(rk_{i+2^k}\) 为第二关键字即可。

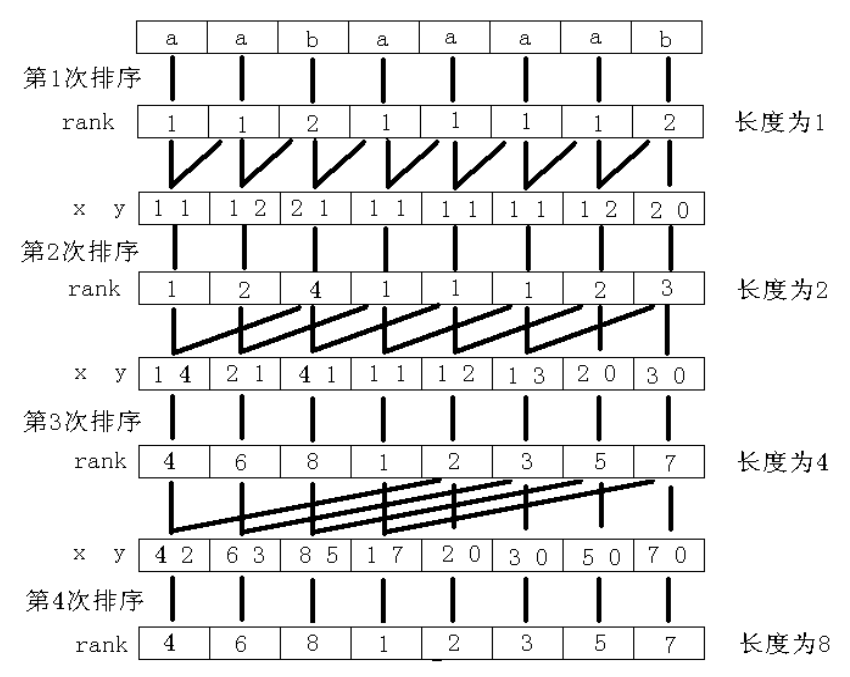
排序用基数排序，总时间 \(O(n\log n)\)

code

#include<algorithm>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1e6+10;
char s[N];
int n,m,p,sa[N],rk[N<<1],ork[N<<1],id[N],cnt[N];
int main() {
	scanf("%s",s+1);
	n=strlen(s+1);
	m=127;
	for(int i=1; i<=n; i++) ++cnt[rk[i]=s[i]];
	for(int i=1; i<=m; i++) cnt[i]+=cnt[i-1];
	for(int i=n; i>=1; i--) sa[cnt[rk[i]]--]=i;
	memcpy(ork+1,rk+1,n*sizeof(int));
	for(int p=0,i=1; i<=n; i++) {
		if(ork[sa[i]]==ork[sa[i-1]]) {
			rk[sa[i]]=p;
		} else {
			rk[sa[i]]=++p;
		}
	}
	for(int w=1; w<n; w<<=1,m=n) {
		memset(cnt,0,sizeof(cnt));
		memcpy(id+1,sa+1,n*sizeof(int));
		for(int i=1; i<=n; i++) ++cnt[rk[id[i]+w]];
		for(int i=1; i<=m; i++) cnt[i]+=cnt[i-1];
		for(int i=n; i>=1; i--) sa[cnt[rk[id[i]+w]]--]=id[i];
		memset(cnt,0,sizeof(cnt));
		memcpy(id+1,sa+1,n*sizeof(int));
		for(int i=1; i<=n; i++) ++cnt[rk[id[i]]];
		for(int i=1; i<=m; i++) cnt[i]+=cnt[i-1];
		for(int i=n; i>=1; i--) sa[cnt[rk[id[i]]]--]=id[i];
		memcpy(ork+1,rk+1,n*sizeof(int));
		for(int p=0,i=1; i<=n; i++) {
			if(ork[sa[i]]==ork[sa[i-1]]&&ork[sa[i]+w]==ork[sa[i-1]+w]) {
				rk[sa[i]]=p;
			} else {
				rk[sa[i]]=++p;
			}
		}
	}
	for(int i=1; i<=n; i++) printf("%d ",sa[i]);
	return 0;
}

code(常数优化)

#include<algorithm>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
const int N=1e6+10;
char s[N];
int n,m,p,sa[N],rk[N<<1],ork[N<<1],id[N],cnt[N];
bool cmp(int x,int y,int w) {
	return ork[x]==ork[y]&&ork[x+w]==ork[y+w];
}
int main() {
	scanf("%s",s+1);
	n=strlen(s+1);
	m=127;
	for(int i=1; i<=n; i++) ++cnt[rk[i]=s[i]];
	for(int i=1; i<=m; i++) cnt[i]+=cnt[i-1];
	for(int i=n; i>=1; i--) sa[cnt[rk[i]]--]=i;
	memcpy(ork+1,rk+1,n*sizeof(int));
	for(int p=0,i=1; i<=n; i++)
		rk[sa[i]]=cmp(sa[i],sa[i-1],0)?p:++p;
	for(int w=1; w<n; w<<=1,m=n) {
		int p=0;
		for(int i=n; i>n-w; i--) id[++p]=i;
		for(int i=1; i<=n; i++) if(sa[i]>w) id[++p]=sa[i]-w;
		memset(cnt,0,sizeof(cnt));
		for(int i=1; i<=n; i++) ++cnt[rk[id[i]]];
		for(int i=1; i<=m; i++) cnt[i]+=cnt[i-1];
		for(int i=n; i>=1; i--) sa[cnt[rk[id[i]]]--]=id[i];
		memcpy(ork+1,rk+1,n*sizeof(int));
		p=0;
		for(int i=1; i<=n; i++)
			rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;
		if(p==n) break;
	}
	for(int i=1; i<=n; i++) printf("%d ",sa[i]);
	return 0;
}

利用后缀数组解决 LCP 问题

\(lcp(i,j)\) 表示 \(i\) 的后缀和 \(j\) 的后缀的最长公共前缀。

LCP Theorem：
\(lcp(i,j)=\min(lcp(sa_k,sa_{k+1}))，sa_i\le sa_k < sa_j\)

设 \(height_i\) 表示 \(lcp(sa_k,sa_{k+1})\).
如果我们能求出 \(height\) 数组，那么任意的 \(lcp\) 就变成 RMQ 问题。

求 \(height\) 的一个引理：
\(h_i\ge h_{i-1}-1\)。

我们已知 \(height_{i-1}\)，设 \(k\) 是 \(i-1\) 在 \(sa\) 数组中的前一个，如图。
已知 \(height_{i-1}=lcp(sa_i,sa_{i-1})\)。
那么 \(i-1,k\) 都把首字母挖掉。变成 \(i,k+1\)。
所以 \(lcp(sa_i,sa_{k+1})=lcp(sa_{i-1},sa_{k})\)，
又因 \(lcp(sa_{i},sa_{k+1})\ge lcp(sa_{i},sa_{i-1})\).
故得证。

所以求 \(height\) 一定是线性复杂度。
再用一些 RMQ 结构即可。

应用

1.P2408 不同子串个数

所有的子串可表示为“任意后缀的任意前缀”。
所以我们先求 SA，然后把 SA 中相邻的 lcp 都减掉即可。

2.P3181 [HAOI2016] 找相同字符

我们先把两个字符串拼起来，中间插一个特殊字符。
先求 SA，然后就变成一个有关 RMQ 的问题。
单调栈，处理出每个 \(height\) 能贡献的区间。
区间两头端点要属不同字符串中。
前缀和计算即可。

3.SP1812 LCS2 - Longest Common Substring II

套路地将所有串拼起来，插入不同的分割符。
然后求 SA。
每个后缀都打一个标记，代表其属于哪个字符串。
考虑尺取法，找到包含所有字符串的区间，然后计算一下 lcp 即可。

4.P2336 [SCOI2012]喵星球上的点名

SA + 莫队。
首先套路地将所有串拼起来，插入不同的分割符，并求 SA.
对于每一个询问，考虑二分找到其的询问区间。
然后莫队可以解决区间数颜色问题。
最后问每个颜色被询问多少次，这个在莫队的过程中在时间轴上面差分即可。

5.CF204E Little Elephant and Strings

同样的尺取法，不过这道题需要正反两次尺取，因为它的 \(K\) 可能不为 \(n\).
当我们尺取到一个区间，那么我们就用线段树记录一下这个区间都是这个答案。