各类 Dp 优化
1.状态设计优化
给个例题:求最长公共子序列,
但是 \(A\) 长度为 \(n=10^6\),\(B\) 长度为 \(m=10^3\)。
\(O(nm)\) 会超时。
不妨设 \(f(i,j)\) 表示取了 \(i\) 个 B,答案是 \(j\),\(A\) 的最小长度。
这样复杂度是 \(O(m^2)\)。
2.斜率优化
以这题为例:P3195 [HNOI2008]玩具装箱
原始方程 \(dp_i=\min(dp_j+(sum_i+i-sum_j-j-L-1)^2)\).
我们设 \(a_i=sum_i+i\)
\(b_i=sum_j+j+L+1\)
\(dp_i=\min(dp_j+(a_i-b_j)^2)\)
设 \(dp_i\) 由 \(dp_j\) 转移而来。
\(dp_i=dp_j+a_i^2-2a_ib_j+b_j^2\)
写成一次函数在y轴截距形式:
\(dp_i-a_i^2=dp_j+b_j^2-2a_ib_j\)
其中\(dp_i-a_i^2\) 为截距, \(b_j\) 为 横坐标 \(dp_j+b_j^2\) 为 纵坐标, \(2a_i\) 为 斜率.
即求最小的截距。
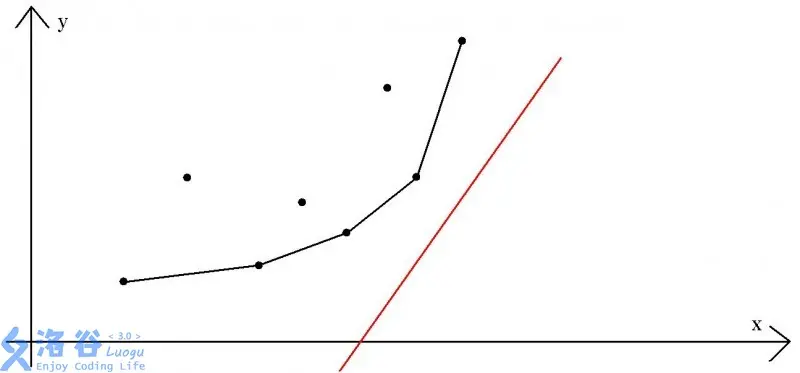
红线为斜率为 \(2a_i\) 的直线。
从下往上移动,碰到第一个点为\(j\).
这时就求得了最小的截距。
\(j\) 与 \(j-1\) 的斜率是不超过 \(2a_i\) 最大的。
于是用单调队列维护凸包。
凸包内的点是不用考虑的。
code
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef double db;
typedef long long LL;
const int N=50010;
int n,L;
db sum[N],dp[N];
int head,tail,Q[N];
db a(int i) {return sum[i]+i;}
db b(int i) {return a(i)+L+1;}
db X(int i) {return b(i);}
db Y(int i) {return dp[i]+b(i)*b(i);}
db slope(int i,int j) {return (Y(i)-Y(j))/(X(i)-X(j));}
int main() {
scanf("%d%d",&n,&L);
for(int i=1; i<=n; i++) {
scanf("%lf",&sum[i]);
sum[i]+=sum[i-1];
}
head=tail=1;
for(int i=1; i<=n; i++) {
while(head<tail&&slope(Q[head],Q[head+1])<2*a(i)) ++head;
dp[i]=dp[Q[head]]+(a(i)-b(Q[head]))*(a(i)-b(Q[head]));
while(head<tail&&slope(i,Q[tail-1])<slope(Q[tail-1],Q[tail])) --tail;
Q[++tail]=i;
}
printf("%lld\n",(LL)dp[n]);
return 0;
}
3.wqs 二分优化
我们以这题为例:CF739E
我们显然有一个 \(O(n^3)\) 的方程,
状态为 \(f(i,j,k)\) 表示前 \(i\) 只神奇宝贝,用了 \(j\) 个宝贝球,\(k\) 个超级球。
答案是 \(f(n,a,b)\).
我们若钦定超级球随便取的话,我们有一个函数 \(g(k)=f(n,a,k)\),表示超级球取了 \(k\) 个。
这是一个上凸函数,故导函数单调下降。
下图显示了 \(g(x)\) 与 \(g'(x)\).
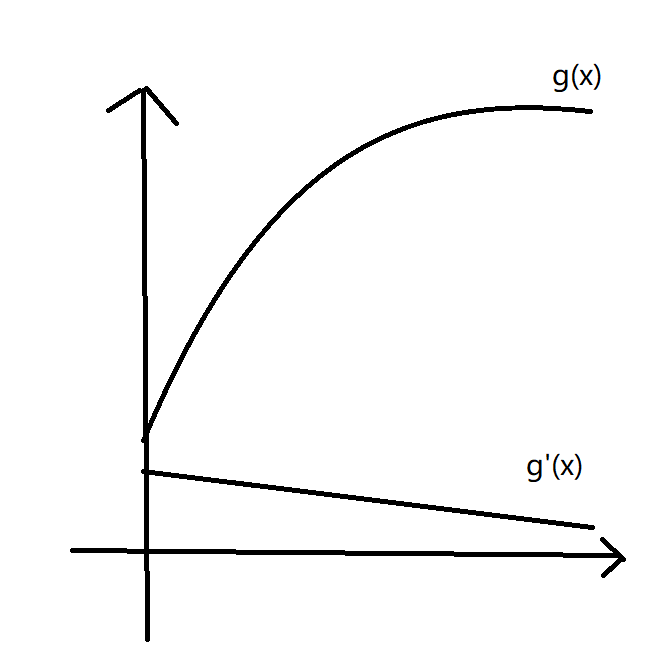
我们的 dp 是可以求出 \(g(x)\) 的最大值以及 \(x\) 的取值的。
此时只有 \(n,a\) 两维,所以时间是 \(O(n^2)\)
如果不加以限制的话,那么我们只能取到 \(k=\infty\).
我们知道当 \(g'(x)=0\) 时,原函数取最大值。
于是我们设计一个新的 \(g(x)=f(n,a,k)-k\cdot t\)
其中 \(t\) 是我们的一个设的系数。
这样 \(g'(x)=g'(x)-t\)。
于是 \(g'(x)\) 的图像向下移动了 \(t\),与 \(x\) 轴交点就不在取 \(\infty\)。
我们二分 \(t\),直到与 \(x\) 轴交点为 \(b\)。
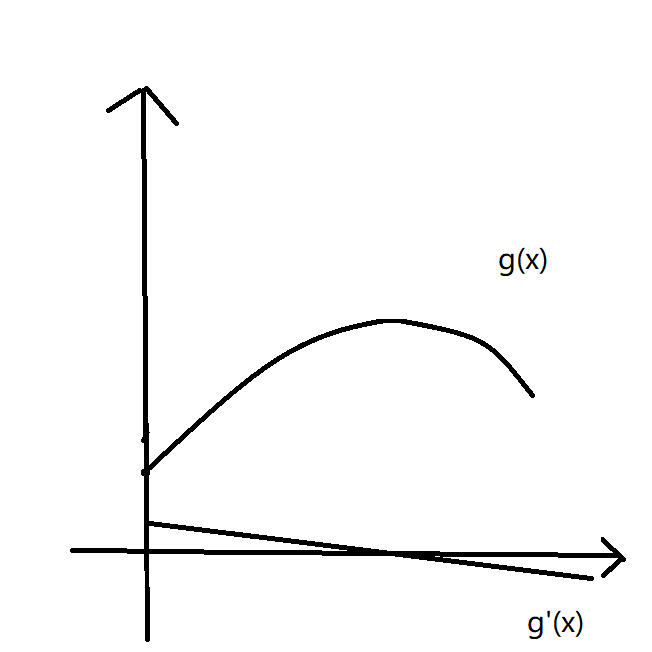
这样我们 dp 就可以求出 \(x=b\) 的取值。
此时 \(g(b)+t\cdot b\) 即为答案。
时间复杂度 \(O(n^2\cdot k)\),将二分次数定为 \(k\).
code
#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
const int N=2000+5;
const double eps=1e-16;
int n,a,b;
double p[N],u[N];
double f[N][N];
int cnt[N][N];
bool check(double mid) {
memset(f,0,sizeof(f));
memset(cnt,0,sizeof(cnt));
for(int i=1; i<=n; i++) {
for(int j=0; j<=a; j++) {
cnt[i][j]=cnt[i-1][j];
f[i][j]=f[i-1][j];
if(j!=0&&f[i-1][j-1]+p[i]>=f[i][j]) {
f[i][j]=f[i-1][j-1]+p[i];
cnt[i][j]=cnt[i-1][j-1];
}
if(j!=0&&f[i-1][j-1]+u[i]+p[i]-u[i]*p[i]-mid>=f[i][j]) {
f[i][j]=f[i-1][j-1]+u[i]+p[i]-u[i]*p[i]-mid;
cnt[i][j]=cnt[i-1][j-1]+1;
}
if(f[i-1][j]+u[i]-mid>=f[i][j]) {
f[i][j]=f[i-1][j]+u[i]-mid;
cnt[i][j]=cnt[i-1][j]+1;
}
}
}
return cnt[n][a]<=b;
}
int main() {
scanf("%d%d%d",&n,&a,&b);
for(int i=1; i<=n; i++) scanf("%lf",&p[i]);
for(int i=1; i<=n; i++) scanf("%lf",&u[i]);
double l=0,r=2,ans=0;
for(int i=1; i<=76; i++) {
double mid=(l+r)/2;
if(check(mid)) r=mid,ans=f[n][a]+r*b;
else l=mid;
}
printf("%.5lf\n",ans);
return 0;
}
4.决策单调性优化
若一个函数 \(w_{i,j}\),满足 \(w_{a,d}+w_{c,d}\ge w_{a,c}+w_{b,d}\),其中 \(a\le b\le c\le d\),
称其满足四边形不等式。
如果有这样的 dp,其转移是 \(f_i=\min f_j+w_{j,i}\),其中 \(w\) 满足四边形不等式,
那么这个 dp 满足决策单调性。
有了决策单调性,我们该怎么办呢。
以 P1912 诗人小G 为例:
采用决策队列优化:
队列维护的是三元组 \((p,l,r)\) 表示 \(l\sim r\) 的最优决策点目前看来都是 \(p\),
初始时队列只有 \((0,1,n)\).
如果现在计算 \(dp_i\),先把队首 \(l<i\) 的弹出,并把新的队首的 \(l\) 设为 \(i\).
\(dp_i\) 应被队首那个点决策。
接下来从队尾开始扫,如果队尾的 \(p\) 在 \(l\) 的决策比 \(i\) 劣,那么 \(p\) 的决策是无用的了,那么就弹出队尾。
最后,队尾的 \(p\) 在 \(l\) 时比 \(i\) 更优,但是在 \(l\sim n\) 里一个位置往后是更劣的。
寻找 \(i\) 在哪里会代替 \(p\) 形成决策,是可以二分的。
设这个点是 \(x\),那么把队尾改成 \((p,l,x-1)\),加入 \((i,x,n)\).
code
#include<bits/stdc++.h>
using namespace std;
typedef long double ld;
const int N=1e5+9;
int n,L,P,s[N],q[N],h,t,lft[N],rig[N],pr[N];
ld f[N];
char str[N][33];
ld qpow(ld b) {
ld a=1;
for(int k=P; k; k>>=1,b*=b)
if(k&1) a*=b;
return a;
}
ld calc(int i,int j) {
return f[j]+qpow(abs(s[i]-s[j]-L));
}
int main() {
cin.tie(0),cout.tie(0);
int T; cin>>T;
while(T--) {
cin>>n>>L>>P; L++;
for(int i=1; i<=n; i++) {
if(scanf("%s",str[i]));
s[i]=s[i-1]+strlen(str[i])+1;
}
h=1,t=1;
q[1]=0,lft[0]=1,rig[0]=n;
for(int i=1; i<=n; i++) {
while(rig[q[h]]<i) ++h;
int now=q[h];
f[i]=calc(i,now);
pr[i]=now;
if(calc(n,q[t])<calc(n,i)) continue;
while(calc(lft[q[t]],q[t])>calc(lft[q[t]],i)) --t;
int Le=lft[now],Ri=n;
while(Le<Ri) {
int mid=(Le+Ri)/2;
if(calc(mid,i)<calc(mid,q[t])) Ri=mid;
else Le=mid+1;
}
rig[q[t]]=Le-1;
q[++t]=i,lft[i]=Le,rig[i]=n;
}
if(f[n]>1e18) puts("Too hard to arrange");
else {
printf("%lld\n",(long long)(f[n]+0.5));
q[t=0]=n;
for(int i=n; i; q[++t]=i=pr[i]);
for(; t; --t) {
int i;
for(i=q[t]+1; i<q[t-1]; i++)
printf("%s ",str[i]);
puts(str[i]);
}
}
puts("--------------------");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号