Splay 平衡树

前置知识

平衡树，顾名思义是一种数据结构。
我们一般讨论的是二叉平衡树。
对于每一个子树来说：左子树的所有数比根小，右子树我的所有数比根大。

Splay

rotate

先介绍 zig，zag.
可以发现 zig 和 zag 是不改变树的中序遍历的。

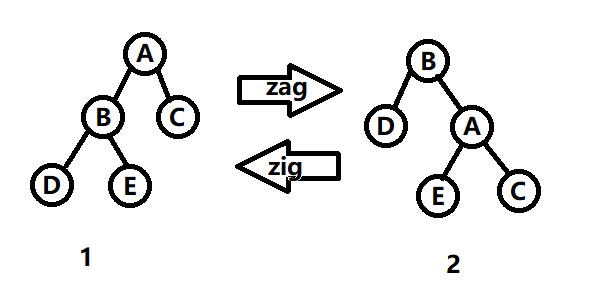
这两个操作构成了 rotate 函数，即把一个元素向上转。

code

bool get(int x) {return ch[fa[x]][1]==x;}
void pushup(int x) {
    if(x) {
        sz[x]=cnt[x];
        if(ch[x][0]) sz[x]+=sz[ch[x][0]];
        if(ch[x][1]) sz[x]+=sz[ch[x][1]];
    }
}
void rotate(int x) {
    int y=fa[x],z=fa[y],k=get(x);
    ch[y][k]=ch[x][k^1]; fa[ch[x][k^1]]=y;
    ch[x][k^1]=y; fa[y]=x;
    fa[x]=z;
    if(z) ch[z][ch[z][1]==y]=x;
    pushup(y); pushup(x);
}

splay

继续，多次 rotate 构成了 splay, 即把一个元素旋转到根节点（伸展）
考虑子节点，父亲节点，和爷爷节点。
若共线，则先转父节点，再转子节点。若不共线，则转两次子节点。
这是为了维护树的平衡。
此外，记得在每次更新信息后要 splay 一下。

code

void splay(int x,int goal=0) {
    for(; fa[x]!=goal; ) {
        int y=fa[x],z=fa[y];
        if(z!=goal) rotate(get(x)==get(y)?y:x);
        rotate(x);
    }
    if(goal==0) rt=x;
}

find

即找到一个数所在位置。
根据平衡树的特性，我们可以在每个节点二分。（类似线段树）
注意找到后要把 splay 一下。
若平衡树里不存在这个数，可能返回它的后继或者前驱。

code

void find(int x) {
    int u=rt;
    if(!u) return ;
    for(; ch[u][x>val[u]]&&x!=val[u]; )
        u=ch[u][x>val[u]];
    splay(u,0);
}

insert

插入一个数。
先找到它所应插入的位置，然后插入，并 pushup，最后 splay.

code

void insert(int x) {
    int u=rt,f=0;
    for(; u&&val[u]!=x; ) {
        f=u;
        u=ch[u][x>val[u]];
    }
    if(u) {cnt[u]++; pushup(u); pushup(f);}
    else {
        u=++tot;
        val[u]=x; sz[u]=cnt[u]=1;
        fa[u]=f; ch[u][0]=ch[u][1]=0;
        if(f) {ch[f][x>val[f]]=u; pushup(f);}
        else rt=u;
    }
    splay(u,0);
}

queryrank

先 find，旋转到根节点。
然后讨论一下 find 找到的是什么。
然后得出答案是根节点左孩子的 siz +1 / 或加上根节点的 cnt

code

int query_rank(int x) {
    find(x);
    if(val[rt]>=x) return sz[ch[rt][0]]+1;
    else return sz[ch[rt][0]]+cnt[rt]+1;
}

querykth

二分（类似线段树）.

code

int query_kth(int x) {
    int u=rt;
    for(; u; ) {
        if(ch[u][0]&&x<=sz[ch[u][0]])
            u=ch[u][0];
        else {
            int tmp=sz[ch[u][0]]+cnt[u];
            if(x<=tmp) {splay(u,0); return val[u];}
            x-=tmp; u=ch[u][1]; 
        }
    }
}

pre/succ

先 find ，转到根节点。
答案是根节点左子树的最大值或右子树的最小值。

code

int pre(int x) {
    find(x);
    if(val[rt]<x) return rt;
    int u=ch[rt][0];
    for(; ch[u][1]; ) u=ch[u][1];
    splay(u,0);
    return u;
}
int succ(int x) {
    find(x);
    if(val[rt]>x) return rt;
    int u=ch[rt][1];
    for(; ch[u][0]; ) u=ch[u][0];
    splay(u,0);
    return u;
}

del

先 find，旋转到根节点。
讨论一下根节点的左右子树情况，最难的是左右子树都有。
那么需要先找原来根节点的前驱，再把前驱旋转到根节点。
放个图：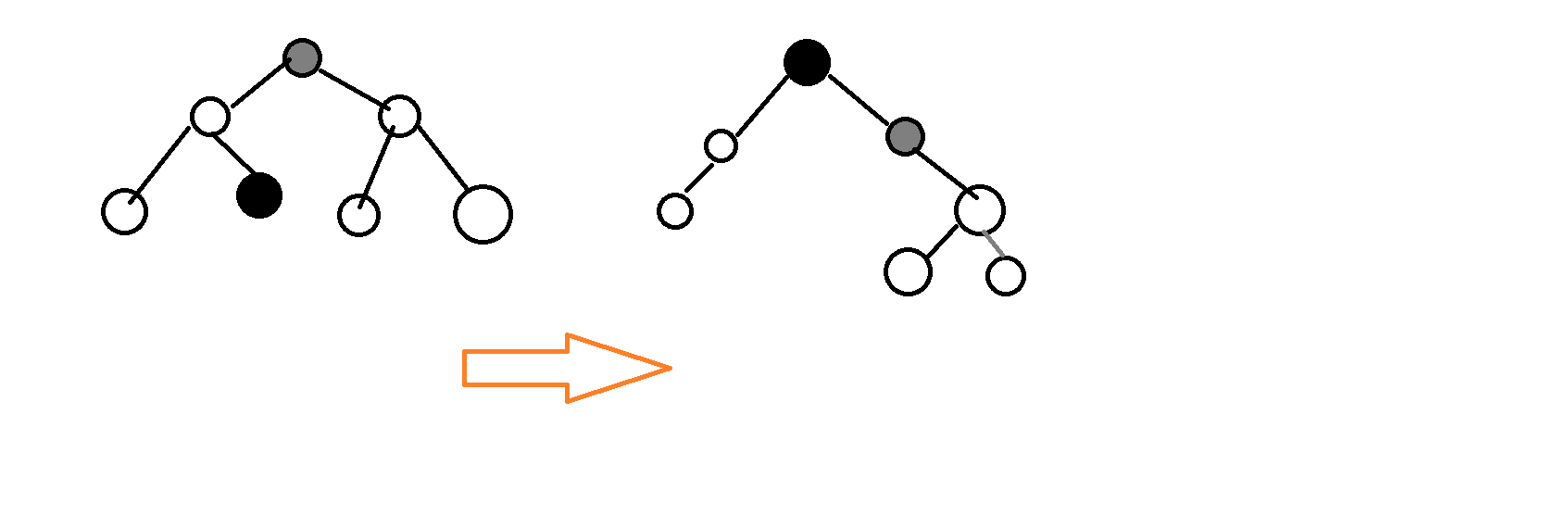
发现前驱，原来的根，原来的根的右儿子共线，且原来的根没有左儿子。
直接删去原来的根即可。
记得操作完一定要 pushup.

code

void del(int x) {
    find(x);
    if(cnt[rt]>1) {cnt[rt]--; pushup(rt); return ;}
    if(!ch[rt][0]&&!ch[rt][1]) {rt=0; return ;}
    if(!ch[rt][0]||!ch[rt][1]) {
        rt=ch[rt][0]?ch[rt][0]:ch[rt][1];
        fa[rt]=0;
        return ;
    }
    int ort=rt,p=pre(x);
    splay(p,0);
    ch[rt][1]=ch[ort][1]; fa[ch[ort][1]]=rt;
    pushup(rt);
}

应用

P6136 【模板】普通平衡树（数据加强版）

模板。

code

#include<bits/stdc++.h>
using namespace std;
const int N=11e5+10;
int n,m,last,ans;
int rt,tot;
int fa[N],ch[N][2],val[N],cnt[N],sz[N];
bool get(int x) {return ch[fa[x]][1]==x;}
void pushup(int x) {
    if(x) {
        sz[x]=cnt[x];
        if(ch[x][0]) sz[x]+=sz[ch[x][0]];
        if(ch[x][1]) sz[x]+=sz[ch[x][1]];
    }
}
void rotate(int x) {
    int y=fa[x],z=fa[y],k=get(x);
    ch[y][k]=ch[x][k^1]; fa[ch[x][k^1]]=y;
    ch[x][k^1]=y; fa[y]=x;
    fa[x]=z;
    if(z) ch[z][ch[z][1]==y]=x;
    pushup(y); pushup(x);
}
void splay(int x,int goal=0) {
    for(; fa[x]!=goal; ) {
        int y=fa[x],z=fa[y];
        if(z!=goal) rotate(get(x)==get(y)?y:x);
        rotate(x);
    }
    if(goal==0) rt=x;
}
void find(int x) {
    int u=rt;
    if(!u) return ;
    for(; ch[u][x>val[u]]&&x!=val[u]; )
        u=ch[u][x>val[u]];
    splay(u,0);
}
void insert(int x) {
    int u=rt,f=0;
    for(; u&&val[u]!=x; ) {
        f=u;
        u=ch[u][x>val[u]];
    }
    if(u) {cnt[u]++; pushup(u); pushup(f);}
    else {
        u=++tot;
        val[u]=x; sz[u]=cnt[u]=1;
        fa[u]=f; ch[u][0]=ch[u][1]=0;
        if(f) {ch[f][x>val[f]]=u; pushup(f);}
        else rt=u;
    }
    splay(u,0);
}
int query_rank(int x) {
    find(x);
    if(val[rt]>=x) return sz[ch[rt][0]]+1;
    else return sz[ch[rt][0]]+cnt[rt]+1;
}
int query_kth(int x) {
    int u=rt;
    for(; u; ) {
        if(ch[u][0]&&x<=sz[ch[u][0]])
            u=ch[u][0];
        else {
            int tmp=sz[ch[u][0]]+cnt[u];
            if(x<=tmp) {splay(u,0); return val[u];}
            x-=tmp; u=ch[u][1]; 
        }
    }
}
int pre(int x) {
    find(x);
    if(val[rt]<x) return rt;
    int u=ch[rt][0];
    for(; ch[u][1]; ) u=ch[u][1];
    splay(u,0);
    return u;
}
int succ(int x) {
    find(x);
    if(val[rt]>x) return rt;
    int u=ch[rt][1];
    for(; ch[u][0]; ) u=ch[u][0];
    splay(u,0);
    return u;
}
void del(int x) {
    find(x);
    if(cnt[rt]>1) {cnt[rt]--; pushup(rt); return ;}
    if(!ch[rt][0]&&!ch[rt][1]) {rt=0; return ;}
    if(!ch[rt][0]||!ch[rt][1]) {
        rt=ch[rt][0]?ch[rt][0]:ch[rt][1];
        fa[rt]=0;
        return ;
    }
    int ort=rt,p=pre(x);
    splay(p,0);
    ch[rt][1]=ch[ort][1]; fa[ch[ort][1]]=rt;
    pushup(rt);
}
int main() {
    scanf("%d%d",&n,&m);
    for(int x; n--; ) {
        scanf("%d",&x);
        insert(x);
    }
    for(int op,x; m--; ) {
        scanf("%d%d",&op,&x);
        x^=last;
        switch(op) {
            case 1: insert(x); break;
            case 2: del(x); break;
            case 3: last=query_rank(x); ans^=last; break;
            case 4: last=query_kth(x); ans^=last; break;
            case 5: last=val[pre(x)]; ans^=last; break;
            case 6: last=val[succ(x)]; ans^=last; break;
        }
    }
    printf("%d\n",ans);
    return 0;
}

这道题维护的是区间序列顺序，所以不能用权值排序了，而要维护的是 splay 的中序遍历。
平衡树可能不满足权值的关系。
怎么翻转一个区间呢？先把其他的元素隔离开罢。
我们把 l-1,r+1 旋转上来。

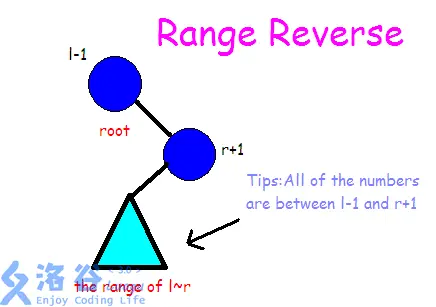
那么就把 l,r 区间打上标记，代表其子树内所有节点需要翻转。
注意：当一个打了标记的节点需要改变位置的时候：一定要标记下传。
最后输出树的中序遍历即可。
注意这里的 find 和模板的 find 不一样。
此处 find 为寻找数列排第 x 的数。

code

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10,inf=1e9;
int n,m;
int rt,tot;
int fa[N],ch[N][2],val[N],cnt[N],sz[N],tag[N];
bool get(int x) {return ch[fa[x]][1]==x;}
void pushup(int x) {
	if(x) {
		sz[x]=cnt[x];
		if(ch[x][0]) sz[x]+=sz[ch[x][0]];
		if(ch[x][1]) sz[x]+=sz[ch[x][1]];
	}
}
void pushdown(int x) {
	if(x&&tag[x]) {
		tag[ch[x][0]]^=1;
		tag[ch[x][1]]^=1;
		swap(ch[x][0],ch[x][1]);
		tag[x]=0;
	}
}
void rotate(int x) {
	int y=fa[x],z=fa[y],k=get(x);
	pushdown(y); pushdown(x);
	ch[y][k]=ch[x][k^1]; fa[ch[x][k^1]]=y;
	ch[x][k^1]=y; fa[y]=x;
	fa[x]=z;
	if(z) ch[z][ch[z][1]==y]=x;
	pushup(y); pushup(x);
}
void splay(int x,int goal) {
	for(; fa[x]!=goal; ) {
		int y=fa[x],z=fa[y];
		if(z!=goal) rotate(get(x)==get(y)?y:x);
		rotate(x);
	}
	if(goal==0) rt=x;
}
int find(int x) {
	int u=rt;
	for(; u; ) {
		pushdown(u);
		if(x<=sz[ch[u][0]]) u=ch[u][0];
		else {
			x-=sz[ch[u][0]]+cnt[u];
			if(!x) return u;
			u=ch[u][1];
		}
	}
}
void insert(int x) {
	int u=rt,f=0;
	for(; u&&val[u]!=x; ) {
		f=u;
		u=ch[u][x>val[u]];
	}
	u=++tot;
	val[u]=x; sz[u]=cnt[u]=1;
	fa[u]=f; ch[u][0]=ch[u][1]=0;
	if(f) {ch[f][x>val[f]]=u; pushup(f);}
	else rt=u;
	splay(u,0);
}
void reverse(int x,int y) {
	int l=find(x-1),r=find(y+1);
	splay(l,0); splay(r,l);
	tag[ch[r][0]]^=1;
}
void dfs(int x) {
	pushdown(x);
	if(ch[x][0]) dfs(ch[x][0]);
	if(val[x]!=-inf&&val[x]!=inf)
		printf("%d ",val[x]);
	if(ch[x][1]) dfs(ch[x][1]);
}
int main() {
	scanf("%d%d",&n,&m);
	insert(-inf);
	for(int i=1; i<=n; i++) insert(i);
	insert(inf);
	for(int i=1,l,r; i<=m; i++) {
		scanf("%d%d",&l,&r);
		reverse(l+1,r+1);
	}
	dfs(rt);
	return 0;
}

posted @ 2023-01-13 10:14 s1monG 阅读(97) 评论(0) 收藏举报

刷新页面返回顶部

simonG

Splay 平衡树

前置知识

Splay

rotate

splay

find

insert

queryrank

querykth

pre/succ

del

应用

P6136 【模板】普通平衡树（数据加强版）

P3391 【模板】文艺平衡树

公告