第2章_003_关系数据库_ 关系代数_002_专门的关系运算

一. 定义 ===》
不仅涉及到行运算，也涉及到列运算，这种运算时为数据库的应用而引进的特殊运算。包括: 选取、投影、连接和除法...等运算。

 

二. 专门关系运算中的行话 ===》
1. 设关系模式为R(A₁, A₂, ..., A_n)，它的一个关系为R。t∈R表示t是R的一个元组(Tuple); t[A_i]表示元组t中相应于属性名为A_i的一个分量(Component)。

2. 从{A₁, A₂, ..., A_n}中选取出来的一部分A = {A_i1, A_i2, ...,A_ik}称为属性列(Attribute Column)，也称域列; {A₁, A₂, ..., A_n}中去掉属性列后的属性组称为剩余属性组，用A一波浪线表示; t[A] = {t[A_i1], t[A_i2], ..., t[A_ik]}表示元组t在属性列A上所有分量的集合。

3. R为目关系，S为m目关系，tr∈R，ts∈S，tr_⌒ts称为元组的连接(concatenation)，它是一个n + m列的元组，前n个分量为R的一个n元组，后m个分量为S中的一个m元组。

4. 给定一个关系R(X, Z)，X和Z为属性组，称Z_{value_x} = {t[Z] | t∈R Λ t[X] = value_x}为value_x在R中的象集(image set)，它表示关系R中的属性组X上值为value_x的所有元组在属性组Z上的分量的集合。我们可以分为2步理解 ===》
　　step_1: 首先它是一个集合，是某一些元组在属性Z上的分量的集合;
　　step_2: 这些元组是关系R中，属性组X上值为value_x的所有元组;

 

 

三. 专门的关系运算符 ===》
1. 选取运算(Selection): (关系式: σ_F(R) = {t | t∈R Λ F(t)=="True"}，其中F为选取条件) ===>
解释: 选取关系R上的一些元组，这些元组能够使得条件F为'真'。

2. 投影运算(Project): 　(关系式: Π_A(R) = {t[A] | t∈R}，A为属性列——我们感兴趣的属性集合) ===>
解释: 我们只想选择关系R中的某几列信息而不是全部信息的时候，就可以将这些列按顺序列在∏的右下角，然后便可以得到这些属性列上所有分量的集合。
投影的特点: 投影后不但减少了属性，元组也可能减少(由于查询的结果是关系，而关系本身就是集合，所以不能存在重复值的元素) ---> 新关系与旧关系不相容。

 

四. 关系中的连接 ===》
1. θ连接(θ就是运算符的代指) ===》
设两个关系为R和S，其中R中的属性可以进一步分解为属性集Z和X，即R = (Z, X)。关系S可以进一步分解为属性集W和Y，即S = (W, Y)。
--(1). 定义: 关系R和S在连接属性X和Y上θ连接，就是值在R和S的广义笛卡尔积中，选取X属性上的分量与Y属性上的分量、并且满足比较条件的那些元组。
--(2). 形式化定义: R ⋈_XθY S = {t_r⌒t_s | t_r∈R Λ t_s∈S Λ t_r[X]θt_s[Y]=="True"}。
--(3). 特点: θ连接是二目运算，是从两个关系的笛卡尔积中选择满足条件的元组，组成新的关系。
--(4). 分类: 当θ作为比较运算符(关系运算符)的时候可分为 ===> >, <, =(等值连接)。
--(5). θ连接的本质: 广义笛卡尔积运算 + 选取运算。即先对两个关系R、S做广义笛卡尔积运算产生新的关系N，再在N中选取满足条件的元组，并形成一个个新的关系。

2. 等值连接 ===》
　　定义: 等值连接是θ连接中的一种特殊的连接，即是当θ取"="时的连接。

3. 自然连接 ===》
--(1). 定义: 在等值连接的情况下，当连接属性X和属性Y具有相同的属性集S时(S = X∩Y)，把连接结果中重复的属性列去掉，形成一个新的表。
--(2). 形式化定义: R ⋈ S = {t_r⌒t_s | t_r∈R Λ t_s∈S Λ t_r[Y]==t_s[Y]}，将其中一个Y列去掉。
--(3). 自然连接的本质: 等值连接 + 去掉重复的属性列。
--(4). "自然连接" VS "等值连接": 自然连接要求相等属性值的属性名相同，但是等值连接不需要，只是要求属性值取自同一个域。

4. 总结 ===》
--(1). 很多时候，我们会利用"自然连接" + "投影运算"来提取我们感兴趣的信息。
--(2). 举例(客户的需求为: 查询教授"数据库"课程的教师姓名) ===》现在我们有3个关系模式:
　　1st. 教师信息关系模式(Teacher):　　　　T(TNo, TN, Sex, Age) ===> TNo: 教师编号; TN:  教师姓名; ...;
　　2nd. 课程信息关系模式(Class): 　　　　 C(CNo, CN, CR, CT) 　===> CNo: 课程标号; CN:  课程名称; ...;
　　3rd. 教师-课程关系模式(Teacher-Class): TC(TNo, CNo)　　　　 ===> TNo: 教师编号; CNo: 课程编号;
(  i). 分析问题: 想要"查询教授'数据库'课程的教师姓名"，首先就要得到教师信息关系模式(Teacher)和课程信息关系模式(Class)，这两个表都有; 单有这两个表肯定不行，我们还需要二者的联系表，当然这个我们也有。所以信息相对来说十分完备，可以解决需求问题。
( ii). 在解决问题之前首先建立一个实体-联系模型(E-R模型)，这样能使各个实体集之间的联系更直观地呈现在我们面前 ===》

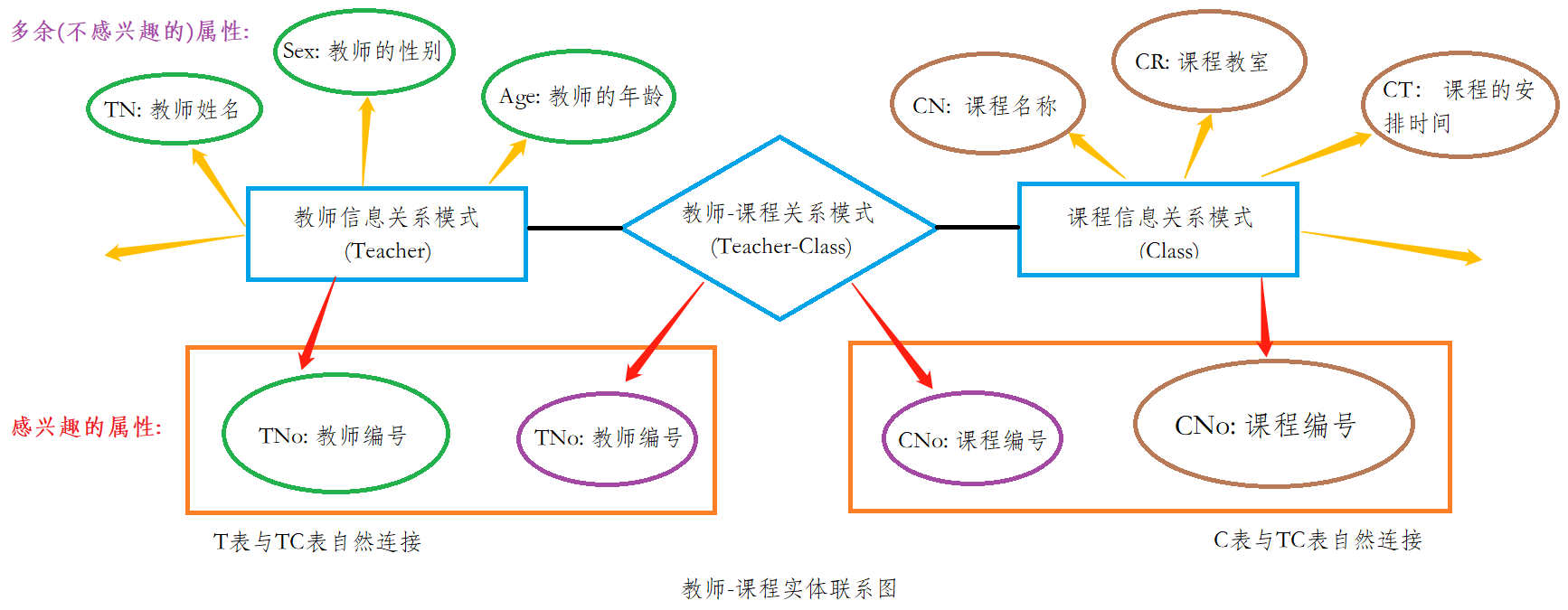
(iii). 不难发现: 虽然有TC表作为T表和C表之间的桥梁，但是TC表中既没有"CN"这个字段，也没有"TN"这个字段，所以我们需要进一步对这三张表进行关系运算。
　　step_1: 由于我们已知课程名称(CN)为"数据库"，所以在C表中我们便可以通过"CN"来确定"CNo";
　　step_2: 确定了"CNo"后，我们就能将C表与TC表通过"CNo"进行自然连接了，从而确定教授"数据库"这门课程的教师的教师编号"TNo";
　　step_3: 与step_2同理，我们得到"TNo"后便能与T表进行自然连接，然后投影出"TN"字段的值的集合;
(iv). 当然啦，在这一过程中，C表和T表中有一些对我们的结果没有作用的属性型(即我们不感兴趣的部分)，这个时候为了不让中间过程产生的数据量过大，我们可以将它们投影掉(即只考虑感兴趣的属性: TNo, TN, CNo, CN)，综上所述，总的表达式为:

Π_TN{Π_TNo[σ_{CN='数据库'}(C) ⋈ TC] ⋈ Π_{TNo, TN}(T)}

 

 

五. 除法 ===》
1. 已知条件: 除法运算是二目运算，设有关系R(X, Y)和关系S(Y, Z)，其中X, Y, Z为属性集合，R中的Y和S中的Y可以有不同的属性名，对应属性必须出出自相同的域。

2. 定义: 关系R除以关系S所得的商是一个新的关系P(X)，P是R中，在属性集X上分量值为value_x的像集Y_{value_x}包含了S在Y上投影的集合的元组在X上的投影。我们可以这样来理解这个除法的定义，分为3步 ===》
　　step_1: 首先它是一个关系，这个关系中有且仅有某些满足特定条件的元组R中在属性集X的的投影;
　　step_2: 在这些元组满足的条件中包含了两个集合 ===》
　　　　1st. 在属性集X上分量值为x的像集Y_{value_x}，value_x为迭代器，遍历属性集X中所有属性值;
　　　　2nd. S在Y上投影的集合S_Y = Π_Y(S);
　　step_3: 条件为: Y_{value_x} ⊇ S_Y;

3. 形式化定义: R ÷ S = {t_r[X] | t_r∈R Λ Π_Y(S)⊆Y_{value_x}}

4. 依据理解定义的3步骤，我们在遇到除法关系运算时可对应的分为3步来解题 ===》
　　step_1: 投影R中的属性集X，得到X上的所有分量的集合;
　　step_2: 依据所得的集合得出value_x在R中的像集Y_{value_x}，再在投影S中的属性集Y，得到Y上的所有分量的集合S_Y;
　　step_3: 挑选出满足条件: "Y_{value_x} ⊇ S_Y"的Y_{value_x}，最后得出相应的value_x的集合并形成新的关系P(X);

5. 适用于包含"全部"和"至少"...等短语的查询。例如 ===》
--(1). 查询选修了全部课程的学生的学号和姓名: 
　　　　Π_{SNo, CNo}(SC) ÷ Π_CNo(C) ⋈ Π_{SNo, SN}(S);
--(2). 查询至少选修了C1课程和C3课程的学生学号:
　　　　Π_{SNo, CNo}(SC) ÷ Π_CNo[σ_{(CNo='C1' ∨ CNo='C3')}(C)];