基础篇_010_函数_函数式编程

----函数式编程是什么 ===》

　　定义：函数式语言(functional language)一类程序设计语言，是一种非冯·诺伊曼式的程序设计语言。函数式语言主要成分是原始函数、定义函数和函数型。这种语言具有较强的组织数据结构的能力，可以把某一数据结构(如数组)作为单一值处理；可以把函数作为参数，其结果也可为函数，这种定义的函数称为高阶函数，程序就是函数，程序作用在结构型数据上，产生结构型结果，从根本上改变了冯·诺伊曼式语言的“逐词”工作方式。——来自"函数式编程语言（functional language）"

　　简单来说就是: 用编程语言来实现数学函数。函数内的对象是永恒不变的，函数的类型属于高阶函数。所有的循环由递归实现，不使用for和while循环。

 

----函数式编程的特点 ===》

　　1. 不可变性: 不用变量来保存任何状态。既然没有了保存状态这一保障，表示变量一经赋值就不能被修改，那么也就是变量不可变。

　　2. 第一类对象: 即函数即变量(这里指的是"函数名"即变量，"函数名"存储函数的地址)。

　　3. 尾部递归调用时的优化(准确来说仅仅只是尾递归调用，并没有优化)。

 

首先来看一下什么是高阶函数 ===》 

----高阶函数: 只要满足"把函数当做参数传给另一个函数 / 返回值当中包含函数"，这个函数就是高阶函数

--(1). 把函数当做参数传给另一个函数 ===》

def foo(arg):
    print(arg)

def foo_arg(arg):
    print("My name is %s" % arg)

foo(foo_arg("SunRan"))
# 输出的结果为：My name is SunRan '\n' None
# print(arg) ===》None
# print("My name is %s" % arg) ===》My name is SunRan

--(2). 返回值当中包含函数 ===》

def foo_first():
    print("from foo_first()")

def foo_second():
    print("from foo_second()")
    return foo_first    # 返回一个函数名

foo_second()()
# "from foo_second()"
# from foo_first()

--(3). 返回值为自己 ===》

def foo():
    print("from foo()")
    return foo

foo()()
# from foo()
# from foo()

 

----尾递归优化: 在最后一步递归 ===》

　　1. 尾调用: 在函数的最后一步调用其他函数，eg: 

def foo_1(n):
    return n
def foo_2(x):
    return foo_1(x)

print(foo_1(2)) # 输出：2　

　　2. 在了解什么尾调用之后，我们来看一下尾调用到底有什么用 ===》

--(1). 普普通通的递归函数:  

# 普普通通的递归函数 ===》
def fact(n):
    if n == 0:
        return 1
    else:
        return n * fact(n - 1)

print(fact(5))  # 输出：120

我们可以这样理解步骤 ===》

step_ 1: fact(5);result = n * fact(4);此时，由于result的值不知道，所以不能return，内存中将会存放fact(5)的状态，跳入fact(4);

step_ 2: fact(4);result = n * fact(3);此时，由于result的值不知道，所以不能return，内存中将会存放fact(4)的状态，跳入fact(3);

step_ 3: fact(3);result = n * fact(2);此时，由于result的值不知道，所以不能return，内存中将会存放fact(3)的状态，跳入fact(2);

step_ 4: fact(2);result = n * fact(1);此时，由于result的值不知道，所以不能return，内存中将会存放fact(2)的状态，跳入fact(1); 

step_ 5: fact(1);result = n * fact(0);此时，由于result的值不知道，所以不能return，内存中将会存放fact(1)的状态，跳入fact(0);

step_ 6: fact(0);此时 n == 0 成立;result = 1;return   1，fact(0) =   1，返回到fact(1);

step_ 7: fact(1);result = 1 * fact(0) =   1; return   1，fact(1) =   1，返回到fact(2);

step_ 8: fact(2);result = 2 * fact(1) =   2; return   2，fact(2) =   2，返回到fact(3);

step_ 9: fact(3);result = 3 * fact(2) =   6; return   6，fact(3) =   6，返回到fact(4);

step_10: fact(4);result = 4 * fact(3) =  24; return  24，fact(4) =  24，返回到fact(5);

step_11: fact(5);result = 5 * fact(4) = 120; return 120，fact(5) = 120，结束得到值 120 ;

 在函数展开的时候，将return n * fact(n - 1)拆成3个步骤: result = fact(n - 1); result = n * result; return result;            我们可以画一下图来帮助我们理解 ===》                                                                                        

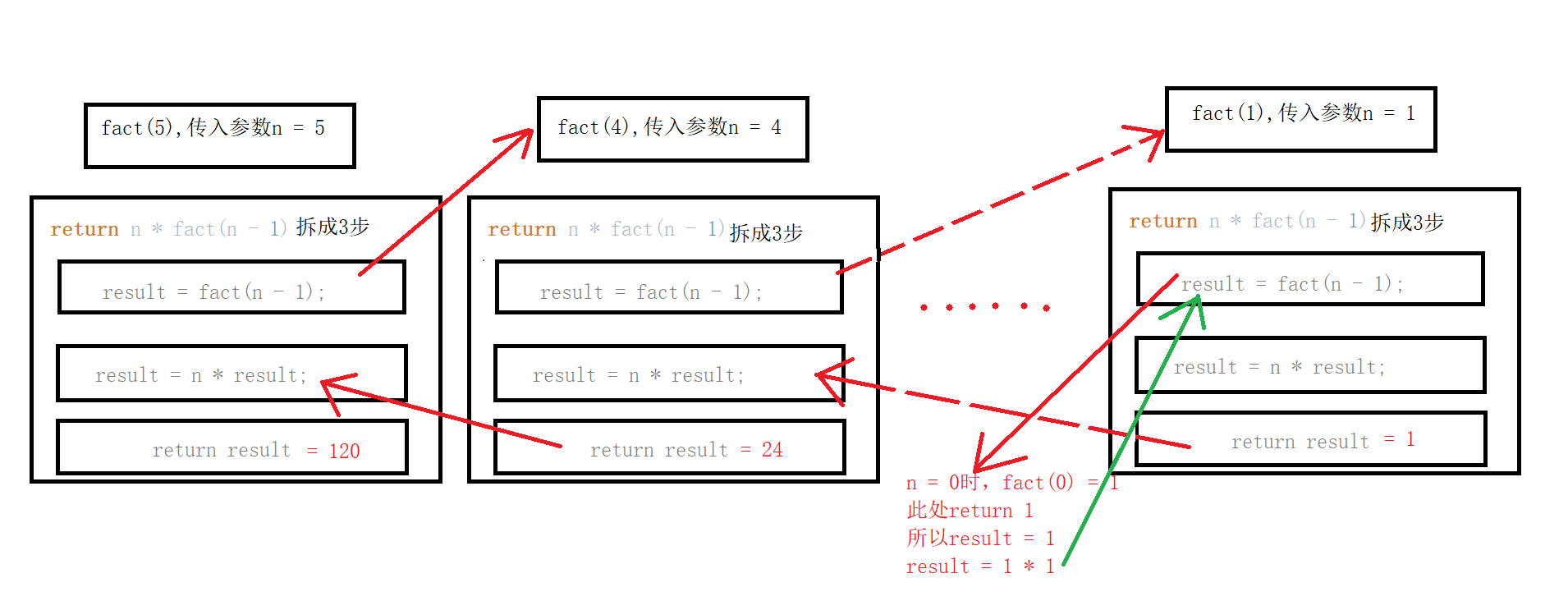
简单来说，当我们计算fact(5)的时候，计算机是这样执行的(这里简单地分为两大步) ===》

first 将函数全部入栈(即将函数展开)                                                                                           　　5 * fact(4);                                                                                           　　            　　 5 * (4 * fact(3));                                                                                           　　             # two thousand years later............                                                                                       5 * (4 * (3 * (2 * (1 * 1)))); // 这就是最终的展开，但这仅仅是函数的展开，还没有开始运算

second 函数运算，一层一层弹出返回值(函数合并)                                                                                      5 * (4 * (3 * (2 * 1)));                          　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　         5 * (4 * (3 * 2));                                                                                           　　             # two thousand years later............                                                                                       120 // 最终的结果...

这样来看，由于函数要保留跳入下一层之前的状态(保存临时变量result...)，导致函数的运行效率很低，如果递归过于庞大的话可能导致栈溢出,eg: fact(n >= 998时)，Python将会报错: RecursionError: maximum recursion depth exceeded in comparison。

--(2). 那有没有一种方法可以解决这种问题呢？这个时候想到尾递归调用 ===》

# 尾递归函数: 在函数的最后一步调用自己 ===》
def fact(n, result = 1):
    if n == 0:
        return result * 1
    else:
        return fact(n - 1, n * result)

print(fact(5))  # 输出：120

来分析这段代码，依旧和上面一样来展开和运算 ===》

first 将函数全部入栈(即将函数展开)                                                                                                  fact(5,   1)                                                                                                                  fact(4,   5)                                                                                                                  fact(3,  20)                                                                                                                  fact(2,  60)                                                                                                                  fact(1, 120)                                                                                                                 fact(0, 120)                                                                                                                  返回值result = 120                                         

诶诶诶，貌似在展开的时候就已经计算完缓存的结果了，使得并不会像普通递归函数那样展开出非常庞大的中间结果，所以不会爆栈是吗？那您可就太天真了，再怎么说您将函数展开那就得将它再合上啊，没毛病叭？所以还有第二步: 合并

second 函数合并(一层一层向上弹出最终的result = 120，直到最顶层fact(5)，然后返回该值)                                               return fact(0, 120) = 120                                                                                                    return fact(1, 120) = 120                                                                                                    return fact(2,  60) = 120                                                                                                    # two thousand years later............                                                                                        return fact(4,   5) = 120                                                                                                    所以最终得到fact(5, 1) = 120

 同理，我们在函数展开的时候可以分成两个步骤: result = fact(n - 1, n * result); return result;                                我们可以画一下图来帮助我们理解 ===》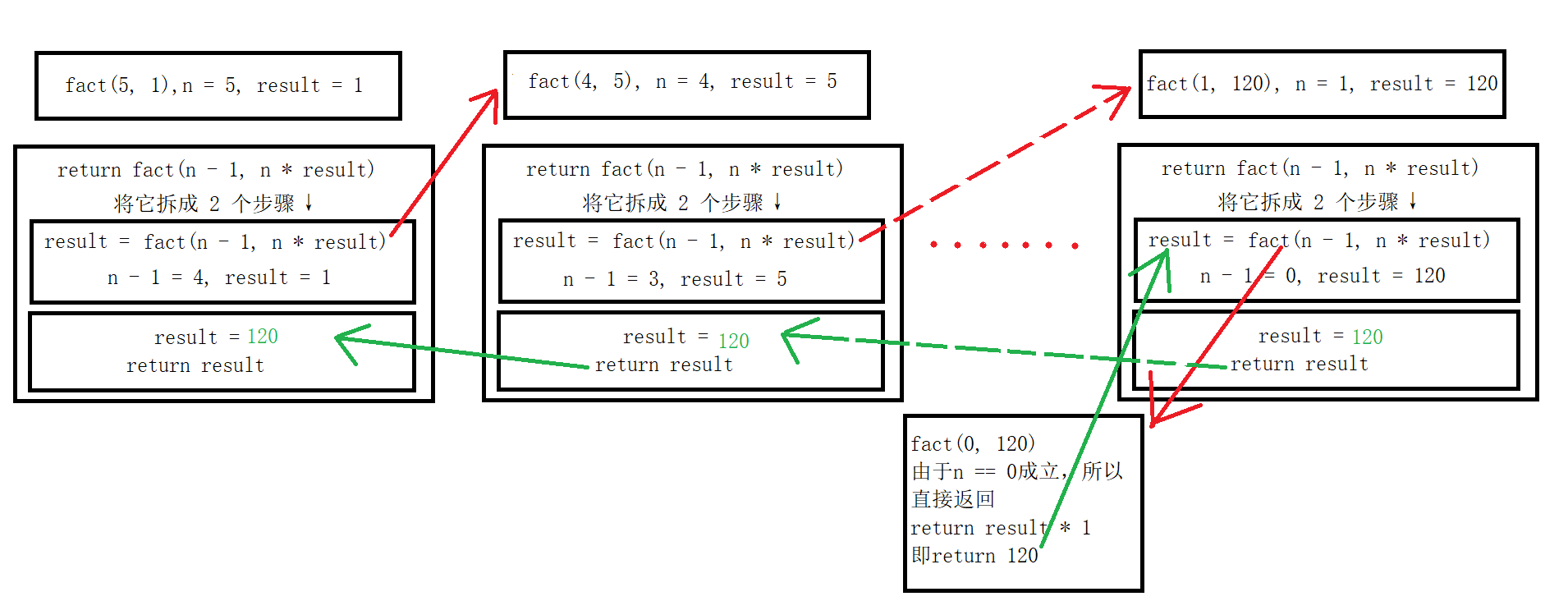                                                                                         

所以尾递归和普通递归没什么两样啊。对，本来就是这样的，因为尾递归函数它依旧还是递归函数的一种，只要是递归函数，那就必须遵循函数栈: 跳进去了你就得弹出来，再怎么说也不能让上层的函数发霉啊。不会像普通递归函数"爆栈"是因为编译器已经给你优化了，如果还是一样"爆栈"的话，那也就只能说明一个问题: 你的编译器很懒(例如Pycharm)。那为啥要把它提出来呢？这里就要牵扯到今日主角: 尾递归优化。

--(3). 尾递归优化===》

在讲尾递归优化之前，我们问一下大家: 函数栈这个栈数据结构的实现，它的作用是什么？可能会有"先进后出" / "解决复杂问题，将其简单化"...答案，这些都没有触及到函数栈的本质意义: 保持入口环境(出自"尾递归为啥能优化？")。

所以当入口环境没有任何意义的时候，我们干嘛还要保持它呢，直接把它优化掉！这种尾递归调用就是这种状况，因为最终我们要的只是最后的结果result = 120，它和这些中间的状态并没有关系(这些中间层的函数只是充当一个"弹射器"，将最后的结果弹到最顶层)。

想要实现尾递归优化其实很简单，就是将递归改成循环(将参数的类型由"递归类型" ---> "迭代类型")，只需要一下几个步骤即可完成 ===》  　　step_1: 将普通递归函数转换成尾递归函数。                                                                                 　　step_2: 在函数中写上一个循环(while True: )，退出循环的条件就是n == 0成立时直接return最后的结果。                             step_3: 将递归函数的参数(此时类型为"递归类型")取出(此时被更改为迭代类型)，然后更新迭代变量。

# 尾递归优化操作: 手动将递归改写成循环 ===》
def fact(n, result = 1):
   while True:
       if n == 0:
           return 1 * result
       else:
           result = n * result
           n = n - 1

print(fact(5))  # 输出：120

# 当然亦可以将更新迭代的操作改成更新函数: updata_fact(updata_n, updata_result) ===》
def fact(n, result = 1):
    def updata_fact(updata_n, updata_result):
       nonlocal  n, result
        n = updata_n
        result = updata_result
    while True:
       if n == 0:
           return 1 * result
       else:
           updata_fact(n - 1, n * result)
            
print(fact(5))  # 输出：120

--(4). 自动尾递归优化 ===》知识有限，等学到一定程度再回来填坑。有兴趣的朋友可以参照一下大佬写的"尾递归为啥能优化？"

最后，我只想说"尾递归优化"就内样儿，不是太喜欢，这纯粹就是在炫技，除了在一些没有循环的纯函数式语言中有意义，比如强类型的Concurrent Clean(外部链接需加速器)、Haskell、Miranda和弱类型的Lazy K。所以...这篇文章...呵呵，或许就是对知识的渴求叭。