Problem.

定义函数

\[f(x)=\begin{cases} \frac12,&\text{if }x<0\\ \frac{f(x-f(x-1))}2,&\text{otherwise} \end{cases} \]

求 \(-\log_2(f(4))\)。

Solution.

定义 \(g(x)=-\log_2(f(x))\)。

一个非常类似燃烧数函数的函数。尝试把他画出来。

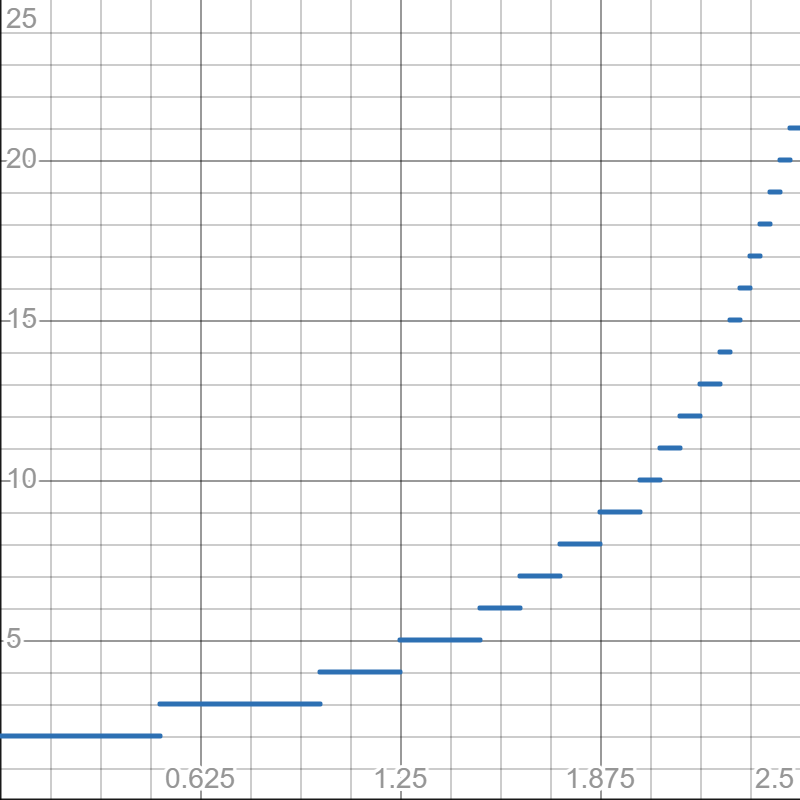
显然这是一个分段函数，每段都有它自己的长度。

\([0,1]\) 被分为两段，\(2\) 和 \(3\) 各占 \(\frac12\)。

\([1,2]\) 被分为六段（两种不同长度），\(4,5\) 各占 \(\frac14\)（总占 \(\frac12\)），\(6,7,8,9\) 各占 \(\frac18\)（总占 \(\frac12\)）。因此 \(g(2)=10\)。

尝试使用相同的方法计算 \(g(3)\)。这也就意味着 \([2,3]\) 被分解为多段（六种不同长度，这与 \([1,2]\) 中的段数对应）。我们可以使用贡献法统计答案。列出表格：

x 的下界 区间长度 \(= 2^{-g(x-1)}\) 区间内的 \(g\) 贡献 \(= \text{区间长度}\times 2^{g}\)
\(-\infty\) \(\text{N/A}\) \(\text{N/A}\) \(10\)
\(1\) \(\tfrac{1}{4}\) \(4\) \(2^{2}\)
\(\tfrac{5}{4}\) \(\tfrac{1}{4}\) \(5\) \(2^{3}\)
\(\tfrac{3}{2}\) \(\tfrac{1}{8}\) \(6\) \(2^{3}\)
\(\tfrac{13}{8}\) \(\tfrac{1}{8}\) \(7\) \(2^{4}\)
\(\tfrac{7}{4}\) \(\tfrac{1}{8}\) \(8\) \(2^{5}\)
\(\tfrac{15}{8}\) \(\tfrac{1}{8}\) \(9\) \(2^{6}\)

这样我们可以得到 \(g(3)=2^6+2^5+2^4+2^3+2^3+2^2+10=142\)。

我们还注意到对于相同的 \(g(x-2)\)（假设位于 \([a,b)\)），\(g(x-1)\) 里面的 \(x\) 增加的贡献是一个等比数列，可以通过 \(x=a\) 处 \(g(x-1)\) 增加的贡献快速求出。对于上述表格就是：

x 的下界 区间长度 \(= 2^{-g(x-1)}\) 区间内的 \(g\) 贡献 \(= \text{区间长度}\times 2^{g}\)
\(1\) \(\tfrac{1}{4}\) \(4\) \(2^{2}\)
\(\left(\times 2:\,[1,\frac32\right)\) \(\tfrac{1}{4}\ \text{each}\) \(\times(2^2-1)=2^4-2^2\)
\(\tfrac{3}{2}\) \(\tfrac{1}{8}\) \(6\) \(2^{3}\)
\(\left(\times 4:\,[\frac32,2\right)\) \(\tfrac{1}{8}\ \text{each}\) \(\times(2^4-1)=2^7-2^3\)

这样我们还是可以得到 \(g(3)=g(2)+(2^7-2^3)+(2^4-2^2)=2^7+14=142\)。

我们可以用同样的方法计算 \(g(4)\)。最后一列省略 \(\times(2^m-1)\)。

x 的下界 区间长度 \(= 2^{-g(x-1)}\) 区间内的 \(g\) 贡献 \(= \text{区间长度}\times 2^{g}\)
\(2\) \(\tfrac{1}{16}\) \(10\) \(2^{6}\)
\(\left(\times 4:\,[2,\tfrac{9}{4})\right)\) \(\tfrac{1}{16}\ \text{each}\) \(2^{10}-2^{6}\)
\(\tfrac{9}{4}\) \(\tfrac{1}{32}\) \(14\) \(2^{9}\)
\(\left(\times 8:\,[\tfrac{9}{4},\tfrac{5}{2})\right)\) \(\tfrac{1}{32}\ \text{each}\) \(2^{17}-2^{9}\)
\(\tfrac{5}{2}\) \(\tfrac{1}{64}\) \(22\) \(2^{16}\)
\(\left(\times 8:\,[\tfrac{5}{2},\tfrac{21}{8})\right)\) \(\tfrac{1}{64}\ \text{each}\) \(2^{24}-2^{16}\)
\(\tfrac{21}{8}\) \(\tfrac{1}{128}\) \(30\) \(2^{23}\)
\(\left(\times 16:\,[\tfrac{21}{8},\tfrac{11}{4})\right)\) \(\tfrac{1}{128}\ \text{each}\) \(2^{39}-2^{23}\)
\(\tfrac{11}{4}\) \(\tfrac{1}{256}\) \(46\) \(2^{38}\)
\(\left(\times 32:\,[\tfrac{11}{4},\tfrac{23}{8})\right)\) \(\tfrac{1}{256}\ \text{each}\) \(2^{70}-2^{38}\)
\(\tfrac{23}{8}\) \(\tfrac{1}{512}\) \(78\) \(2^{69}\)
\(\left(\times 64:\,[\tfrac{23}{8},3)\right)\) \(\tfrac{1}{512}\ \text{each}\) \(2^{133}-2^{69}\)

因此 \(g(4)=2^{133}+2^{69}+2^{38}+2^{23}+2^{16}+2^9-2^6+g(3)=\boxed{2^{133}+2^{69}+2^{38}+2^{23}+2^{16}+590}\)。

扩展

想要算出 \(g(5)\)，我们只需要知道 \([2,3]\) 中 \(g\) 的阶梯是怎样的。上表中有写：

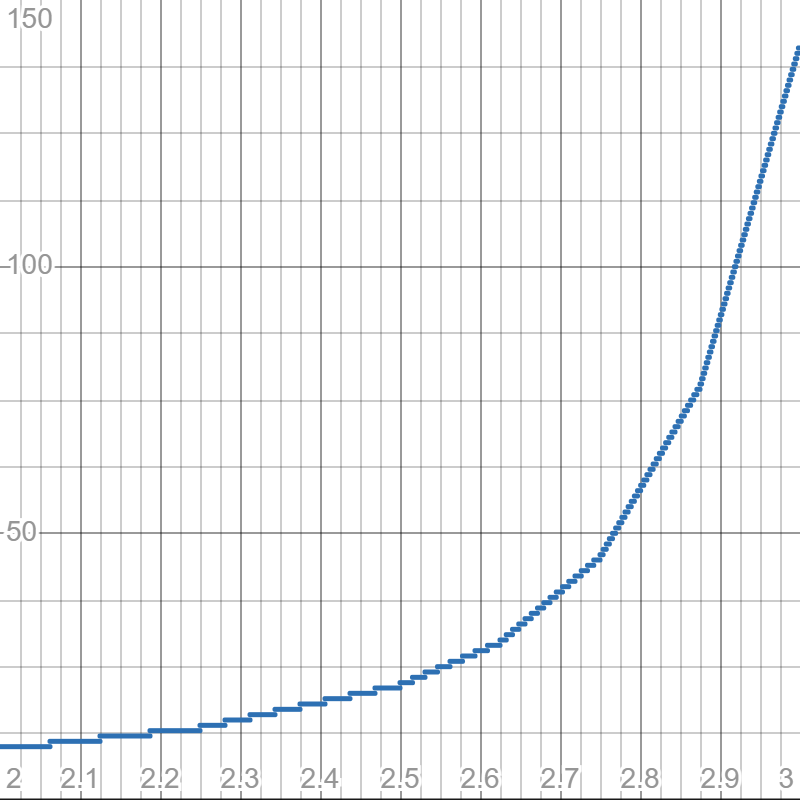
增长的临界点是这样的：

[2, 33/16, 17/8, 35/16, 9/4, 73/32, 37/16, 75/32,19/8, 77/32, 39/16, 79/32, 5/2, 161/64, 81/32,
163/64, 41/16, 165/64, 83/32, 167/64, 21/8, 337/128, 169/64, 339/128, 85/32, 341/128, 171/64, 
343/128, 43/16, 345/128, 173/64, 347/128, 87/32, 349/128, 175/64, 351/128, 11/4, 705/256, 353/128, 
707/256, 177/64, 709/256, 355/128, 711/256, 89/32, 713/256, 357/128, 715/256, 179/64, 717/256, 
359/128, 719/256, 45/16, 721/256, 361/128, 723/256, 181/64, 725/256, 363/128, 727/256, 
91/32, 729/256, 365/128, 731/256, 183/64, 733/256, 367/128, 735/256, 23/8, 1473/512, 
737/256, 1475/512, 369/128, 1477/512, 739/256, 1479/512, 185/64, 1481/512, 741/256, 1483/512, 
371/128, 1485/512, 743/256, 1487/512, 93/32, 1489/512, 745/256, 1491/512, 373/128, 1493/512, 
747/256, 1495/512, 187/64, 1497/512, 749/256, 1499/512, 375/128, 1501/512, 751/256, 1503/512, 
47/16, 1505/512, 753/256, 1507/512, 377/128, 1509/512, 755/256, 1511/512, 189/64, 1513/512, 
757/256, 1515/512, 379/128, 1517/512, 759/256, 1519/512, 95/32, 1521/512, 761/256, 1523/512, 
381/128, 1525/512, 763/256, 1527/512, 191/64, 1529/512, 765/256, 1531/512, 383/128, 1533/512, 767/256, 1535/512]

我们需要对每一段计算出贡献。先写代码：

f(x)=if(x<0,1/2,f(x-f(x-1))/2);
count=0;
arr=Vec(0,132);
last_i=1024;
last_fi=1/1024;
for(i=1024,1536,if(f(i/512)!=last_fi,count=count+1;arr[count]=last_i/512;last_i=i;last_fi=f(i/512)));
arr

得到上方增长的临界点。再写代码：

arr = ...

def compute():
    start = 10
    ret_pos = [133,69,38,23,16,9,6,3,2,1]
    ret_neg = []
    glb = 142
    arr.append(3)
    for i in range(len(arr)):
        lb = arr[i]
        if lb == 3: break
        contrib = glb - start
        count_len = round((arr[i + 1] - arr[i]) * 2**start)
        ret_pos.append(count_len + contrib)
        ret_neg.append(contrib)
        start = start + 1
        glb += count_len
    for i in range(len(ret_pos)):
        try:
            ret_neg.remove(ret_pos[i] - 1)
            ret_pos[i] -= 1
        except:
            pass
    ret_pos.sort(reverse=True)
    return (ret_pos, ret_neg)
(pos, neg) = compute()
assert len(neg) == 0
for a in pos[:-1]: print(f"2^{{%d}} +" % a, end=" ")
print("2^%d" % pos[-1])

得到结果

\[\begin{aligned} &g(5)\\ &=2^{10889035741470030831418283248450174779841} + 2^{5444517870735015416004289529541883396545}\\ &+ 2^{2722258935367507708297292670087737704898} + 2^{1361129467683753854443794240360664859075}\\ &+ 2^{680564733841876927517045025497128436164} + 2^{340282366920938464053670418065360224709}\\ &+ 2^{170141183460469232321983114349476118982} + 2^{85070591730234616456139462491534066119}\\ &+ 2^{42535295865117308523217636562563039688} + 2^{21267647932558654556756723598077526473}\\ &+ 2^{10633823966279327573526267115834769866} + 2^{5316911983139664081911038874713391563}\\ &+ 2^{2658455991569832336103424754152702412} + 2^{1329227995784916463199617693872357837}\\ &+ 2^{664613997892458526747714163732185550} + 2^{332306998946229558521762398662099407}\\ &+ 2^{166153499473115074408786516127056336} + 2^{83076749736557832352298574859534801}\\ &+ 2^{41538374868279211324054604225774034} + 2^{20769187434139900809932618908893651}\\ &+ 2^{10384593717070245552871626250453460} + 2^{5192296858535417924341129921233365}\\ &+ 2^{2596148429268004110075881756623318} + 2^{1298074214634297202943257674318295}\\ &+ 2^{649037107317443749376945633165784} + 2^{324518553659017022593789612589529}\\ &+ 2^{162259276829803659202211602301402} + 2^{81129638415196977506422597157339}\\ &+ 2^{40564819207893636658528094585308} + 2^{20282409604241966234580843299293}\\ &+ 2^{10141204802416131022607217656286} + 2^{5070602401503213416620404834783}\\ &+ 2^{2535301201046754613626998424032} + 2^{1267650600818525212130295218657}\\ &+ 2^{633825300704410511381943615970} + 2^{316912650647353161007767814627}\\ &+ 2^{158456325618824485820679913956} + 2^{79228163104560148227135963621}\\ &+ 2^{39614081847427979430363988454} + 2^{19807041218861895031978000871}\\ &+ 2^{9903520904578852832785007080} + 2^{4951760747437331733188510185}\\ &+ 2^{2475880668866571183390261738} + 2^{1237940629581190908491137515}\\ &+ 2^{618970609938500771041575404} + 2^{309485600117155702316794349}\\ &+ 2^{154743095206483167954403822} + 2^{77371842751146900773208559}\\ &+ 2^{38686216523478767182610928} + 2^{19343403409644700387312113} + 2^{9671996852727666989662706}\\ &+ 2^{4836293574269150290838003} + 2^{2418441935039891941425652} + 2^{1209516115425262766719477}\\ &+ 2^{605053205617948179366390} + 2^{302821750714290885689847} + 2^{151706023262462238851576}\\ &+ 2^{76148159536547915432441} + 2^{38369227673590753722874} + 2^{19479761742112172868091}\\ &+ 2^{10035028776372882440700} + 2^{5312662293503237227005} + 2^{2951479052068414620158}\\ &+ 2^{1770887431351003316735} + 2^{1180591620992297665024} + 2^{590295810633592013313}\\ &+ 2^{295147905454239187458} + 2^{147573952864562774531} + 2^{73786976569724568068}\\ &+ 2^{36893488422305464837} + 2^{18446744348595913222} + 2^{9223372311741137415}\\ &+ 2^{4611686293313749512} + 2^{2305843284100055561} + 2^{1152921779493208586}\\ &+ 2^{576461027189785099} + 2^{288230651038073356} + 2^{144115462962217485} + 2^{72057868924289550}\\ &+ 2^{36029071905325583} + 2^{18014673395843600} + 2^{9007474141102609} + 2^{4503874513732114}\\ &+ 2^{2252074700046867} + 2^{1126174793204244} + 2^{563224839782933} + 2^{281749863072278}\\ &+ 2^{141012374716951} + 2^{70643630539288} + 2^{35459258450457} + 2^{17867072406042}\\ &+ 2^{9070979383835} + 2^{4672932872732} + 2^{2473909617181} + 2^{1374397989406} + 2^{824642175519}\\ &+ 2^{549764268576} + 2^{274886361633} + 2^{137447408162} + 2^{68727931427} + 2^{34368193060}\\ &+ 2^{17188323877} + 2^{8598389286} + 2^{4303421991} + 2^{2155938344} + 2^{1082196521}\\ &+ 2^{545325610} + 2^{276890155} + 2^{142672428} + 2^{75563565} + 2^{42009134} + 2^{25231919}\\ &+ 2^{16843312} + 2^{8454705} + 2^{4260402} + 2^{2163251} + 2^{1114676} + 2^{590389} + 2^{328246}\\ &+ 2^{197175} + 2^{131640} + 2^{66105} + 2^{33338} + 2^{16955} + 2^{8764} + 2^{4669} + 2^{2622} + 2^{1599}\\ &+ 2^{1088} + 2^{577} + 2^{322} + 2^{195} + 2^{132} + 2^{69} + 2^{38} + 2^{23} + 2^{16} + 590 \end{aligned} \]

注意到最大的那个幂次刚好等于 \(g(4)-g(3)+1\)。这点在 \(g(4)\) 同样成立：\(133=142-10+1\)。这个的证明可以通过表格的最后一行发现。