图像去噪

图像去噪

实验目的

(1) 熟悉和掌握 Matlab 图像处理的基本操作；

(2) 掌握 DCT 变换的基本性质和 Matlab 的实现方法；

(3) 掌握如何利用 DCT 变换进行简单的图像去噪任务；

(4) 掌握如何利用 Matlab 进行 PSNR 等图像质量评价客观标准。

实验内容

对 Lena 图像进行基础的图像处理操作，对图像进行添加噪声、去噪处理的操作，并计算去噪处理之后图像与添加噪声前图像的 PSNR。

实验原理

1. 数字图像的表示

一幅图像可以被定义为一个二维函数𝑓(𝑥, 𝑦)，其中𝑥和𝑦是平面坐标，𝑓在每一个坐标处的取值𝑘∈𝑅^𝑟即为图像在该点的亮度和色彩。灰度图像对于每一个坐标𝑥, 𝑦有𝑓(𝑥, 𝑦) = 𝑘∈𝑅来代表图像的灰度信息。同样的，RGB 彩色图像可以看作是一幅图像在三原色通道上的不同灰度图像的加和。

自然灰度图像关于𝑥, 𝑦和幅度连续，但将自然图像转化为数字图像时，需要将坐标和振幅进行数字化处理，通过采样和量化将灰度图像变为一个𝑚 × 𝑛矩阵。Matlab 的矩阵类型可用于数字图像的表达，作为 Matlab 基本数据类型的数值数组本身十分适于表达图像，矩阵的元素和图像的像素之间有着十分自然的对应关系。根据图像数据矩阵的解释方法不同，Matlab 中有如下的四种图像：亮度图像、二值图像、索引图像、RGB 图像。

(1) 亮度图像：一幅亮度图像是一个数据矩阵，其归一化的取值表示亮度。根据其数据类型的不同有着不同的取值范围，如 uint8 类有整数取值范围[0,255]，uint16 类有整数取值范围[0,65535]。规定双精度浮点类归一化图像取值范围[0,1]浮点数；

(2) 二值图像：一幅二值图像是一个取值只有 0 和 1 的逻辑数组，其数据类型必须为 logical；

(3) 索引图像：一幅索引图像是一个数据矩阵，通过其中的取值进行有限的颜色映射，根据索引值进行索引图像的输出，最多仅能有 256 种颜色；

(4) RGB 图像：RGB 图像又称真彩图像，它利用 R、G、B 三个分量来表示一个颜色，通过 RGB 三种基本颜色可以组合出任意颜色。对一个大小为的真彩图像来说，在 Matlab 中的存储为一个的矩阵，其中三颜色分量存储在矩阵的第三维中。

2. 图像处理操作 Matlab 中的实现

（1）DCT变换：

对于二维 DCT 变换有：

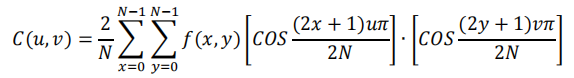
在 Matlab 中有相应的 DCT 函数直接完成相应的任务，在二维信号上，可以利用二维离散余弦变换 dct2()函数或者通过 DCT 变换核的可分离性计算变换矩阵进行计算。

（2）PSNR值计算：

峰值信噪比，在Matlab中可直接调用psnr()函数进行计算。

（3）图像灰度化：

图像灰度化是将一幅彩色图像转换为灰度图像的过程。灰度图像只包含一个通道，通道值表示灰度值。在灰度化过程中，每个像素的RGB值被组合成一个单一的灰度值。在Matlab中图像灰度化可以直接调用rgb2gray()函数进行计算。

实验结果与分析

1.读取 Lena 图像，将彩色图转换为灰度图。

利用imread()函数读入原图，然后利用rgb2gray()函数即可将图片转换为灰度图。原图片与转换后的图片分别如下图左右所示：

2.添加均值为 0，标准差𝜎分别为 10、20、30、40 的高斯噪声。

首先将噪声的标准差𝜎进行0~255的归一化。调用库函数imnoise(I,'gaussian',m,var_gauss)即可为灰度图添加高斯噪声。此处需要注意的是,var_gauss中需要填写的为方差。

添加噪声后的图像如下所示：

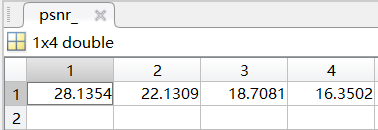
3.计算不同噪声下的图像的 PSNR 值。

直接调用Matlab中的psnr(A,ref)函数即可进行计算。上述4幅添加高斯噪声后的图像的PSNR值分别如下（1,2,3,4分别对应𝜎为10,20,30,40的情况）：

4.图像去噪：对噪声图像进行 DCT 变换（8×8 图像块尺寸），按照3𝜎阈值对变换域上的系数进行处理。对处理后的系数进行 DCT 反变换，得到去噪后的图像。

首先利用循环，将图像分割成8×8尺寸的小图像块，然后对每个小图像块的系数进行DCT变换，并利用3𝜎阈值对变换域上的系数进行判断和处理。对处理后的每个小图像块的系数进行DCT反变换，再将每个小图像块拼接即可得到去噪后的图像。去噪后的图像如下图所示：

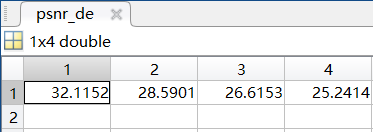
5.计算去噪之后的图像的 PSNR 值。

直接调用Matlab中的psnr(A,ref)函数即可进行计算。上述4幅去噪之后的图像的PSNR值分别如下（1,2,3,4分别对应𝜎为10,20,30,40的情况）：

思考题

1. 在分块 DCT 的条件下还有什么方式可以进行图像去噪？

答：进行图像去噪的方法大致有三大类：基于滤波器的方法、基于模型的方法和基于学习的方法。其中，基于滤波器的方法包括中值滤波和维纳滤波等，基于模型的方法试图对自然图像或噪声的分布进行建模，基于学习的方法侧重于学习有噪声图像到干净图像的潜在映射。

1. 实验中的去噪方法会对原图像造成什么影响？

答：实验中的去噪方法3𝜎阈值滤波法为基于滤波器的方法，该方法可能会导致图像的模糊。该方法对图像进行低通滤波，抑制高频分量，从而降低噪声。但是，这也会使图像的边缘和纹理变得模糊，，导致一些信号信息被误判为噪声而丢失，降低了图像的清晰度和保真度。

源代码

clear();

lena=imread("lena512color.png");

figure;

subplot(1,2,1)

imshow(lena);

lena_gray=rgb2gray(lena);

subplot(1,2,2)

imshow(lena_gray);

figure;

sigma=[10,20,30,40];

sigma_nom=sigma/255;

lena_noised = cell(1, 4);

psnr_=zeros(1,4);

for i=1:4

lema_noise=imnoise(lena_gray,'gaussian',0,sigma_nom(i)^2);

subplot(2,2,i)

imshow(lema_noise)

title(['加噪图像 (σ=', num2str(sigma(i)), ')']);

lena_noised{i}=lema_noise;

psnr_(i)=psnr(lema_noise,lena_gray);

end

figure

block_size=8;

[height, width] = size(lena_gray);

psnr_de=zeros(1,4);

for i=1:4

threshold = 3*sigma(i);

denoised=zeros(height, width);

for y = 1:block_size:height

for x = 1:block_size:width

block = lena_noised{i}(y:y+block_size-1, x:x+block_size-1);

dct_block = dct2(double(block));

dct_block(abs(dct_block) < threshold) = 0;

denoised_block = idct2(dct_block);

denoised(y:y+block_size-1, x:x+block_size-1) = denoised_block;

end

end

subplot(2,2,i)

imshow(uint8(denoised))

title(['去噪图像 (σ=', num2str(sigma(i)), ')']);

psnr_de(i)=psnr(uint8(denoised),lena_gray);

end