[CF1260D] A Game with Traps

A Game with Traps の 传送门

首先，假设带 \(p\) 个人可以，那么带更少的人一定可以。

那么，可以二分带多少个人。

设当前二分带 \(x\) 个人。

带敏捷值最大的 \(x\) 个士兵肯定最好。

先去除当前无用的陷阱，即 \(d_i\) 小于等于 \(x\) 个士兵中的最小敏捷值。

陷阱区间不相交时

然后就是自己从 \(l_i\) 走到 \(r_i\) 解除这个陷阱，再走回来

陷阱区间相交时

看一看下面这个。

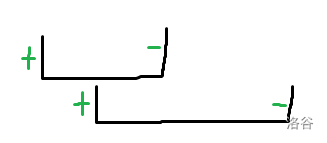
肯定不会从一个一个地从每个区间左边走到右边。

而是从第一个区间左边一直走到第二个区间右边。

写的时候直接左右端点差分，加贡献时对 \(2\) 取个 \(\min\)（往返总共走 \(2\) 次）。

#include <bits/stdc++.h>
#define int long long
#define mid (l + r >> 1)
using namespace std;
inline int read()
{
    int f = 0, ans = 0;
    char c = getchar();
    while (!isdigit(c))
        f |= c == '-', c = getchar();
    while (isdigit(c))
        ans = (ans << 3) + (ans << 1) + c - 48, c = getchar();
    return f ? -ans : ans;
}
void write(int x)
{
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        write(x / 10);
    putchar(x % 10 + '0');
}
constexpr int N = 2e5 + 5, inf = 1e18;
int m, n, k, t, a[N];
int adj[N];
struct trap
{
    int l, r, d;
} b[N];
inline bool check(int x)
{
    int mn = a[x], ti = n + 1;
    for (int i = 1; i <= k; ++i)
        if (mn < b[i].d)
            adj[b[i].l] += 2, adj[b[i].r + 1] -= 2;
    for (int i = 1; i <= n; ++i)
        adj[i] += adj[i - 1], ti += min(adj[i], 2ll);
    for (int i = 1; i <= n; ++i)
        adj[i] = 0;
    return ti <= t;
}
signed main()
{
    // freopen(".in", "r", stdin);
    // freopen(".out", "w", stdout);
    m = read(), n = read(), k = read(), t = read();
    for (int i = 1; i <= m; ++i)
        a[i] = read();
    sort(a + 1, a + m + 1, greater<>());
    a[0] = inf;
    for (int i = 1; i <= k; ++i)
        b[i].l = read(), b[i].r = read(), b[i].d = read();
    int l = 0, r = m, it = -1;
    while (l <= r)
        check(mid)
            ? (it = mid, l = mid + 1)
            : (r = mid - 1);
    write(it);
    return 0;
}