【C】递归

递归

递归的案例

• 汉诺塔
  

• 谢尔斯宾基三角形

  

• 目录树的索引

• 递归自拍照

递归的实质

递归从原理上来说就是函数调用自身这么一个行为

void recursion(void);
void recursion(void)
{
    static int count = 10; //静态局部变量
    printf("Hi!\n");
    if (--count)  //count减1不为0则执行
    {
        recursion(); //函数调用自身
        //一共调用9次
    }
}
int main(void)
{
    recursion(); //启动函数
    return 0;
}

运行结果

Hi!
Hi!
Hi!
Hi!
Hi!
Hi!
Hi!
Hi!
Hi!
Hi!

注意：递归必须要有结束条件，否则程序将崩溃

编写递归程序需要注意的地方

递归程序需要正确设置结束条件，否则递归程序会一直走下去，直到耗尽所有内存崩溃。

递归求阶层

• 写一个求阶乘的函数

  • 正整数阶乘指从1乘以2乘以3乘以4一直乘到所要求的整数。比如所给的数字是5，则阶乘是1×2×3×4×5，得到的积是120，所以120是5的阶乘

  long fact(int num);
  long fact(int num)
  {
      long result;  //阶乘会比较大，用long型
      if (num>0)
      {
          result = num * fact(num-1); //调用自身
      }
      else
      {
          result = 1;
      }
      return result;
  }
  int main(void)
  {
      int num;
      printf("请输入一个正整数 : ");
      scanf("%d",&num);
      printf("%d的阶乘是 : %d",num,fact(num));
  }
  

• 假设我们num的值传入的是5，那么：

  • fact(5) = 5 * fact(4)
    • fact(4) = 4 * fact(3)
      • fact(3) = 3 * fact(2)
        • fact(2) = 2 * fact(1)
          • fact(1) = 1* fact(0)
            • fact(0) = 1

实现递归要满足两个基本条件

• 调用函数本身
• 设置了正确的结束条件

递归的优势和劣势

• 优势：递归的思考角度跟通常的迭代（你可以理解为 for 循环之类的）迥然不同，所以有时候使用迭代思维解决不了的问题，使用递归思维则一下子迎刃而解。
• 劣势：递归的执行效率通常比迭代低很多，所以递归程序要更消耗时间；由于递归函数是不断调用函数本身，在最底层的函数开始返回之前，程序都是一直在消耗栈空间的，所以递归程序要“吃”更多的内存空间；递归的结束条件设置非常重要，因为一旦设置错误，就容易导致程序崩溃。

递归求解汉诺塔

汉诺塔游戏相关内容此处不作介绍

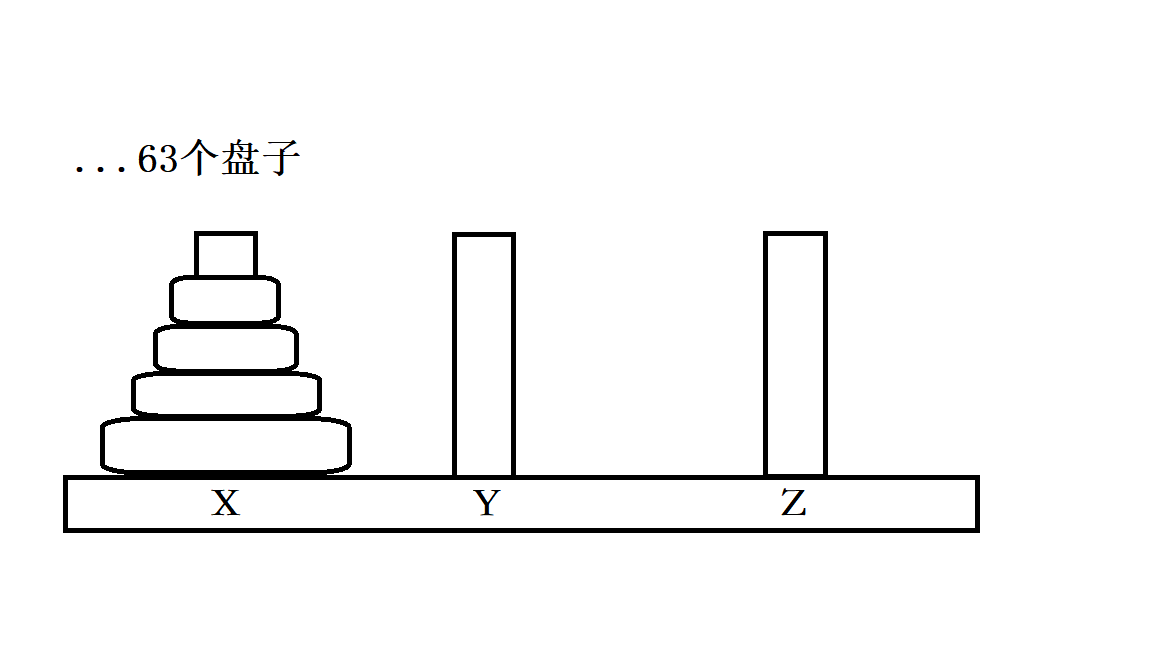
• 对于游戏的玩法，我们可以简单分为三个步骤：

  1. 将前63个盘子从X移动到Y上
  2. 将最底下的第64个盘子从X移动到Z上
  3. 将Y上的63个盘子移动到Z上

• 问题一：将X上的63个盘子借助Z移动到Y上

• 问题二：将Y上的63个盘子借助X移动到Z上

• 将 问题一（”将X上的63个盘子借助Z移动到Y上“）拆解为：

  • 将前62个盘子从X移动到Z上
  • 将最底下的第63个盘子移动到Y上
  • 将Z上的62个盘子移动到Y上

• 将 问题二（”将Y上的63个盘子借助X移动到Z上“）拆解为：

  • 将前62个盘子从Y移动到X上
  • 将最底下的第63个盘子移动到Z上
  • 将X上的62个盘子移动到Z上

void hanoi(int n, char x, char y, char z);// n个盘子
void hanoi(int n, char x, char y, char z)
{
    //hanoi(n,'X','Y','Z')
    if (n == 1)
    {
        printf("%c --> %c\n", x, z);
    }
    else
    {
        hanoi(n-1, x, z, y);
        //hanoi(n-1,'X','Z','Y') 
        printf("%c --> %c\n",x,z);
        hanoi(n-1,y,x,z);
    }
}
int main(void)
{
    int n;
    printf("请输入汉诺塔的层数: ");
    scanf("%d",&n);
    hanoi(n,'X','Y','Z');
    return 0;
}