具有神经网络思维的Logistic回归
第二周神经网络编程基础
来源:CSDN(何宽)
\(author:Sheldon\)
本文是我的个人理解
在正式谈神经网络之前,我们必须重新开始说一下逻辑回归
逻辑回归中的梯度下降
我们首先先来考虑只有一个样本的情况,稍后我们再来谈如果有m个样本该怎么做。
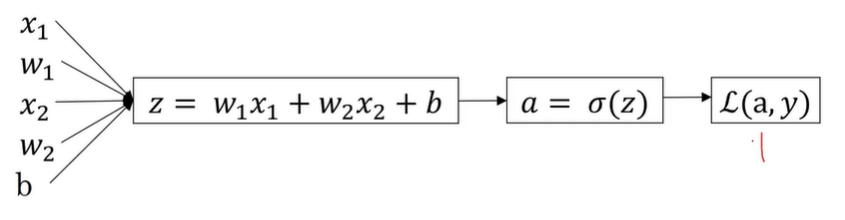
假设我们有一个上述的一个逻辑回归:那么我们可以得到如下的三个式子
\(z=w^{T}x+b\)
\(\hat{y}=a=\sigma(z)\)
\(L(a,y)=-(ylog(a)+(1-y)log(1-a))\)
在这个例子中我们假设只有两个特征\(x_1和x_2\)
为了计算\(z\)我们需要输入参数\(w_1,w_2,b,x_1,x_2\)
那么这里的\(z=w_1x_1+w_2x_2+b\)只是我们\(w\)用的向量的形式表示
相信前向传播大家应该都不会陌生,我们只需要计算出\(L\)这个参数即可
那么前向传播的代码如下
# 注:我们先考虑 m = 1的情况,下述代码是考虑m = m的情况,读者可自行把m看成1
def propagate(w,b,X,Y):
"""
w - 表示权重 这里w.shape = (样本属性个数,1)
b - 偏移量 是一个标量
X - 我们的样本 X.shape = (样本属性个数,训练样本的个数)
Y - 标签 是一个向量 Y.shape = (1,训练样本个数)
"""
m = X.shape[1] # 这样我们得到有多少个训练样本个数
# 不知道为什么A这么表示,看上面的公式
A = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))
#...未完待续...
需要解释的是上述的A是一个标量
接下来我们来讨论一下反向传播:
在\(logistic\)回归中我们需要做的是变换参数\(w\)和\(b\)的值,来最小化损失函数
下面我们讨论如何向后,计算偏导数
我们一步一步计算:
-
首先我们先来计算\(L\)对\(a\)求导
已知的式子:
\(L(a,y)=-(ylog(a)+(1-y)log(1-a))\)
求导后得到如下式子:
\(da=\frac{dL(a,y)}{da}=-\frac{y}{a}+\frac{1-y}{1-a}\)
-
计算\(a\)对\(z\)求导
已知的式子:
\(a=\sigma(z)=\frac{1}{1+e^{-z}}\)
求导后得到如下式子:
\(a^{'}=[\frac{1}{1+e^{-t}}]^{'}=(1+e^{-z})^{-2}e^{-t}=\frac{e^{-t}}{(1+e^{-z})^{2}}=a(1-a)\)
-
通过链式法则我们可以得到\(L\)对\(z\)求导
\(dz=\frac{dL(a,y)}{dz}=\frac{dL}{da}\frac{da}{dz}=(-\frac{y}{a}+\frac{1-y}{1-a})a(1-a)=a-y\)
- 反向传播的最后一步,来计算\(w\)和\(b\)是如何变化的
\(dw_1=\frac{\partial L}{\partial w_1}=\frac{dL}{da}\frac{da}{dz}\frac{dz}{dw_1}=\frac{dL}{dz}\frac{dz}{dw_1}=x_1dz\)
同理可得
\(dw_2=x_2dz\)
\(db=dz\)
-
那么我们可以通过梯度下降更新我们的\(w\)和\(b\)
\(w_1:=w_1-\alpha dw_1\)
\(w_2:=w_2-\alpha dw_2\)
\(b:=b-\alpha db\)
这样我们就完成了我们的反向传播
代码如下
# 注:我们先考虑 m = 1的情况,下述代码是考虑m = m的情况,读者可自行把m看成1
def propagate(w,b,X,Y):
"""
w - 表示权重 这里w.shape = (样本属性个数,1)
b - 偏移量 是一个标量
X - 我们的样本 X.shape = (样本属性个数,训练样本的个数)
Y - 标签 是一个向量 Y.shape = (1,训练样本个数)
"""
m = X.shape[1] # 这样我们得到有多少个训练样本个数
# 不知道为什么A这么表示,看上面的公式
A = (- 1 / m) * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))
#...续上...
dw = (1 / m) * np.dot(X, (A - Y).T) # w的形状和dw是一样的
db = (1 / m) * np.sum(A - Y)
# 最后我们使用字典把dw和db保存起来
grads = {
"dw":dw,
"db":db
}
return (grads,cost)
至此我们就定义好了我们的函数
以上则是只有一个样本的情况
接下来我们来讨论m个样本的情况
我们可以使用最笨的方法,使用for i in range(m)这样我们就可以遍历所有的样本,求出一个dw和db然后再进行迭代。这样做的缺点就是太慢了。因此我们要使用向量化
再次强调我们的损失函数\(J\)是一个标量
我们需要把每个样本的预测值与实际值进行计算,通过累加得到最终的损失函数,因此表达式如下
\(J=\frac{1}{m}\sum_{i=1}^{m}L(a^{(i)},y^{(i)})=(-y^{(i)}log(a^{(i)})-(1-y^{(i)})log(1-a^{(i)}))\)

dw的向量表示
我们知道只有一个样本时
\(dw_1=\frac{\partial L}{\partial w_1}=\frac{dL}{da}\frac{da}{dz}\frac{dz}{dw_1}=\frac{dL}{dz}\frac{dz}{dw_1}=x_1dz\)
\(dz=(a-y)\)
那么有m个样本的话,可得
\(dw_1=x_1dz_1\)
\(dw_2=x_2dz_2\)
\(...\)
\(dw_m=x_mdz_m\)
写成向量
\(dw_{n×1}=X_{n×m}(A-Y)^{T}_{m×1}\)
那么到这里我想你对公式推导有了一定的理解,完整代码及实例见CSDN(何宽)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号