CF1537C 题解

题意

给你一个序列，求满足以下条件的排列：

条件 1：序列首项和末项的差值的绝对值最小。

条件 2：满足条件 1 下，序列中满足 \(a_i<a_{i+1}\) 的项数最大。

条件 3：满足条件 1、2 下，序列的字典序最小。

思路

因为输入时的排列顺序对答案并没有影响，所以可以先排个序。

条件 1 很好想，直接取差最小的相邻两项。假设是 \(a_i\) 和 \(a_{i+1}\) 吧。

然后开始考虑条件 2。

最好的情况是从首项到末项一直上升，但这是不可能的，因为首项和末项取了相邻两项。

于是我们只好退而求其次，考虑只在中间断开一次，两边单调上升。

容易想到可以把排序后的序列以 \(a_i\) 和 \(a_{i+1}\) 为分界线分成两部分，只有 \(a_1\) 和 \(a_n\) 断开了，其他都保持单调上升。

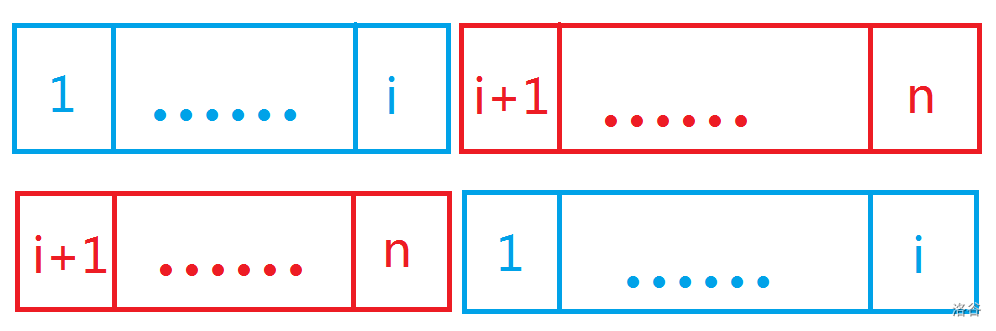
然后我们发现调换 \(a_{i+1}\) 和 \(a_i\) 的位置后依然满足条件 2，而且字典序更小。

但是我不会证明这样为什么字典序最小

上代码。

#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;

int t,n,a[20002];

int main() {
	scanf("%d",&t);
	while(t--) {
		scanf("%d",&n);
		for(int i=1;i<=n;i++) scanf("%d",&a[i]);
		sort(a+1,a+n+1);
		int l,r,minn=2147483647;
		for(int i=1;i<n;i++) 
			if(a[i+1]-a[i]<minn) l=i,r=i+1,minn=a[r]-a[l];
		printf("%d ",a[l]);
		for(int i=r+1;i<=n;i++) printf("%d ",a[i]);
		for(int i=1;i<l;i++) printf("%d ",a[i]);
		printf("%d\n",a[r]);
	}
	return 0;
}