[APIO/CTSC2007]动物园

##题面
洛谷P3622
BZOJ1151
LOJ#10174
##题意
动物园里有n只动物从1到n编号。有c个小朋友，每个小朋友可以看到连续的5只动物(所在的围栏)。其中有他们各自喜欢的和不喜欢的。
现在可以扔掉一些动物(围栏还在)，然后对于1个小朋友，只要看到1只他喜欢的动物还在，或者一只他不喜欢的动物被扔了，他就会高兴...求最多让几个小朋友高兴。
##补充
似乎有很多人被出题人一句不经意的话误导了...

“你可以选择将一些动物从围栏中移走以使得小朋友不会害怕。但你不能移走所有的动物，否则小朋友们就没有动物可看了。”

在数据中，这句话是假的...也就是说，我们其实是可以把所有动物都扔掉的.
##分析
特别像网络流...当场被数据范围踩在脚下
发现5非常非常小，考虑状压dp，算起来复杂度很妙的样子~。
我们对于每一个围栏的位置i,显然在i上的小朋友能看到的区间为$$\left{\begin\left [ i,i+4 \right ], & i\leq n-4\ \left [ i,i+4-n \right ], & n-4<i \leq n\end\right.$$
即**[i,(i+4)%n]我们可以把这5个值状压在一起，在每一位上用0/1表示一只动物扔/不扔。
接着能很快得到dp状态：用f[i][j]表示从位置i开始的5个位置状态为j时，从位置1到i的最多的高兴的小朋友的数量**。
从i-1转移到i，只需讨论i-1位置是否取即可。很容易yy出fake的转移方程：\(f[i][j]=max\lbrace f[i-1][j>>1],f[i-1][(j>>1)+16]\rbrace+i点的贡献\)
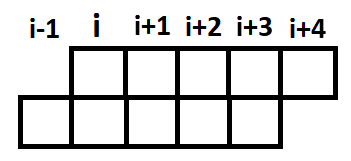
将就着看
(j>>1取出了前4位状态，是否加16决定了i-1位是否为1)

###为什么能加上i点的贡献？(或为什么不加别的点的贡献)(或为什么我这么菜)
因为直到枚举到i时，在位置i的小朋友能看到的5个围栏才都包括在了状态中，固可以只考虑i点，防止答案的遗漏和重复计算。
###那么问题来了：如何计算i点贡献？
~~很简单，~~在读入小朋友喜欢和不喜欢的动物时，直接预处理出g[i][j]表示i位置看到的5只动物的状态为j时，能让多少待在i的小朋友高兴。

---

最后，由于动物园是个环，我们要先枚举一个断点的状态才能往后转移，并且转移一圈回来之后最后的答案也必须取枚举的那个状态。
##代码

#include <iostream>
#include <cstdio>
#include <cctype>
#define il inline
#define vd void
#define rep(i,x,y) for(register int i=x;i<=y;++i)
#define drp(i,x,y) for(register int i=x;i>=y;--i)
using namespace std;
const int Len=2333333,mn=1e4+5;
char buf[Len],*p1=buf,*p2=buf,duf[Len],*q1=duf;
il char gc(); il int rd(); il vd pc(char c); il vd rt(int x); il vd flush();
template<class T> il T Max(T a,T b){return a>b?a:b;}
int n,c,id,a,b,x,y,ans,f,g[33][mn],dp[3][33];
int main(){
	n=rd(),c=rd();
	while(c--){
		id=rd(),a=rd(),b=rd(),x=y=0;
		while(a--) x|=1<<4-(rd()-id+n)%n; //(rd()-id+n)%n为结束点编号，用4去减实现了反转
		while(b--) y|=1<<4-(rd()-id+n)%n;
		rep(j,0,31) if(~j&x||j&y) ++g[j][id]; //~是优先级高的按位取反
	}//我的dp滚了一维，大家自行吐槽
	rep(o,0,31){
		rep(i,0,31) dp[0][i]=-2e9; 
		dp[0][o]=f=0; //除了状态o以外的状态都为极小值(不可达到)，位置0其实对应位置n
		rep(i,1,n){f^=1;
			rep(j,0,31) dp[f][j]=Max(dp[f^1][j>>1],dp[f^1][(j>>1)+16])+g[j][i];
		}
		ans=Max(ans,dp[f][o]); //最后算一圈又算出dp[n][o]
	}
	rt(ans);
	return flush(),0;
}

il char gc(){return p1==p2&&(p2=(p1=buf)+fread(buf,1,Len,stdin),p1==p2)?-1:*p1++;}
il int rd(){char c; int f=1;
	while(!isdigit(c=gc())&&c!='-');
	c=='-'?f=-1,c=gc():0; int x=c^48;
	while(isdigit(c=gc())) x=((x+(x<<2))<<1)+(c^48);
	return x*f;
}
il vd pc(char c){q1==duf+Len&&fwrite(q1=duf,1,Len,stdout),*q1++=c;}
il vd rt(int x){x<0?pc('-'),x=-x:0,pc((x>=10?rt(x/10),x%10:x)+48);}
il vd flush(){fwrite(duf,1,q1-duf,stdout);}