[每日随题15] 前缀和 - 拓扑排序 - 树状数组

整体概述

• 难度：1000 \(\rightarrow\) 1500 \(\rightarrow\) 2000

---

1567B. MEXor Mixup

• 标签：前缀和

• 前置知识：无

• 难度：Div.2.B 1000

题目描述：

输入格式：

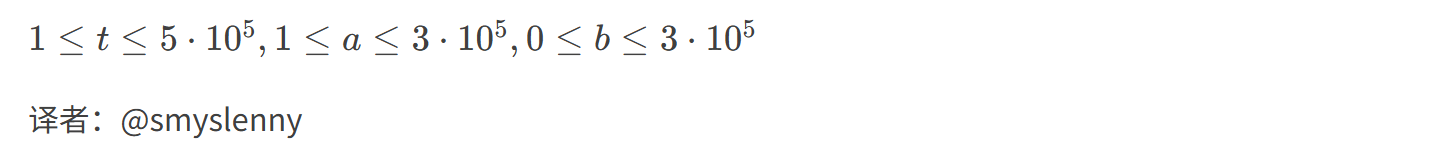
输出格式：

样例输入：

5
1 1
2 1
2 0
1 10000
2 10000

样例输出：

3
2
3
2
3

解题思路：

• 首先我们知道，想要让 \(MEX=a\) 则 \([0,a-1]\) 范围内的数都得选，发现 \(1\le a\le 3·10^5\) 那么我们可以预处理出所有 \([0,x]\) 的异或和。

• 接着要让 \(xor=b\)，我们设 \(xor_{i=0}^a-1=c\)，那么还差 \(b^c\) 就可以凑出该数字。

• 需要注意的是如果 \(c=a\)，那么我们需要拿两个数字凑出 \(c\)，否则只需要直接再增加一个 \(c\) 即可。

  如果 \(c=0\) 表示直接凑出 \(b\) 了，那么不需要再加数字了。

• 预处理出前缀异或和，查询复杂度 \(O(1)\)，总复杂度 \(O(3·10^5)\)。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 3e5+5;
int pre[N];
inline void solve(){
	int a,b; cin >> a >> b;
	int c = pre[a-1]^b;
	if(!c) cout << a << '\n';
	else if(c == a) cout << a+2 << '\n';
	else cout << a+1 << '\n';
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int T; cin >> T;
	for(int i=1;i<N;i++) pre[i] = pre[i-1]^i; 
	while(T--) solve();
	return 0;
}

---

501C. Misha and Forest

• 标签：拓扑排序

• 前置知识：STL-priority_queue

• 难度：Div.2.C 1500

题目描述：

输入格式：

输出格式：

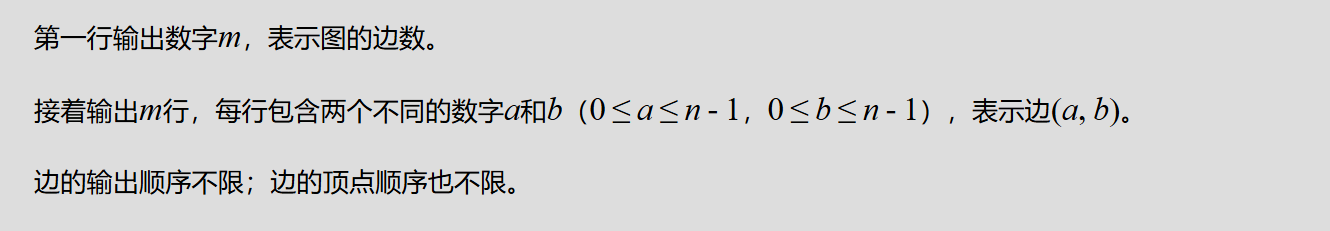
样例输入：

3
2 3
1 0
1 0

2
1 1
1 0

样例输出：

2
1 0
2 0

1
0 1

解题思路：

• 由于是一片森林，不存在环，那么一定有某些节点的度为 \(1\)，而我们又知道这些节点的相邻节点编号的异或和，就是相邻节点的编号，那么这些边就都可以确定了。

• 接着在未确定的边中删去这些边，就会又有某些节点度为 \(1\)，这个过程其实就是拓扑排序的过程，我们跑一遍拓扑排序，每次连边即可。

  需要注意的是，如果出队列的点度为 \(0\) 表明已经连过了，此时跳过即可。

• 总复杂度 \(O(n)\)。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = (1<<16)+5;
int n,d[N],eor[N];
vector<pair<int,int>> res;
inline void solve(){
	cin >> n;
	for(int i=0;i<n;i++) cin >> d[i] >> eor[i];
	queue<int> qu;
	for(int i=0;i<n;i++) if(d[i] == 1) qu.push(i);
	while(!qu.empty()){
		int u = qu.front(); qu.pop();
		int v = eor[u];
		if(!d[u]) continue;
		res.push_back({u,v});
		eor[v] ^= u;
		if(--d[v] == 1) qu.push(v);
	}
	cout << res.size() << '\n';
	for(auto [u,v]:res) cout << u << ' ' << v << '\n';
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int T; T = 1;
	while(T--) solve();
	return 0;
}

---

755D. PolandBall and Polygon

• 标签：树状数组

• 前置知识：无

• 难度：8VC Venture Cup 2017.D 2000

题目描述：

输入格式：

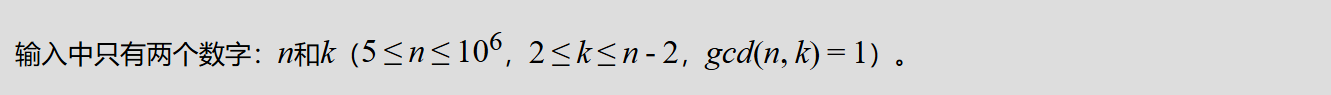
输出格式：

样例输入：

5 2

10 3

样例输出：

2 3 5 8 11 

2 3 4 6 9 12 16 21 26 31 

解题思路：

• 通过画图我们发现，\(画一条线增加的区域数\) 等同于 \(与原有线段的交点个数+1\)，所以问题就转化为每次给出线段的两个端点，求有多少个交点。

• 我们发现所有相交线段的两个端点分别位于线段两侧，即有且仅有一个端点在新线段的 \((l,r)\) 间。由于每条线段两个端点间的距离是固定的，因此我们仅需统计在 \((l,r)\) 内的节点的总度数，即为交点个数。

  需要注意的是，我们用的 \([l,r]\) 区间需要是劣弧的那一段。

• 那么我们用树状数组进行单点修改，区间查询，总复杂度 \(O(n·log_{2}n)\)。

完整代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5;
int n,k,tr[N];
inline void add(int x,int v){
	for(int i=x;i<=n;i+=i&-i) tr[i] += v;
}
inline long long sum(int l,int r){
	if(l > r) return 0;
	long long ans = 0;
	for(int i=r;i;i&=i-1) ans += tr[i];
	for(int i=l-1;i;i&=i-1) ans -= tr[i];
	return ans;
}
inline void solve(){
	cin >> n >> k;
	long long ans = 1;
	for(int i=1,p=1,l,r,cur;i<=n;i++){
		l = p,r = p = l+k > n ? l+k-n : l+k;
		if(l > r) swap(l,r);
		cur = (r-l-1) <= (n-r+l-1) ? sum(l+1,r-1) : sum(r+1,n) + sum(1,l-1); 
		ans += cur+1;
		cout << ans << ' ';
		add(l,1), add(r,1);
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int T; T = 1;
	while(T--) solve();
	return 0;
}

---