[每日随题13] 博弈论 - 二分 - 拓扑排序

整体概述

• 难度：1000 \(\rightarrow\) 1400 \(\rightarrow\) 1500

---

P1288 取数游戏 II

• 标签：博弈论

• 前置知识：无

• 难度：橙 1000

题目描述：

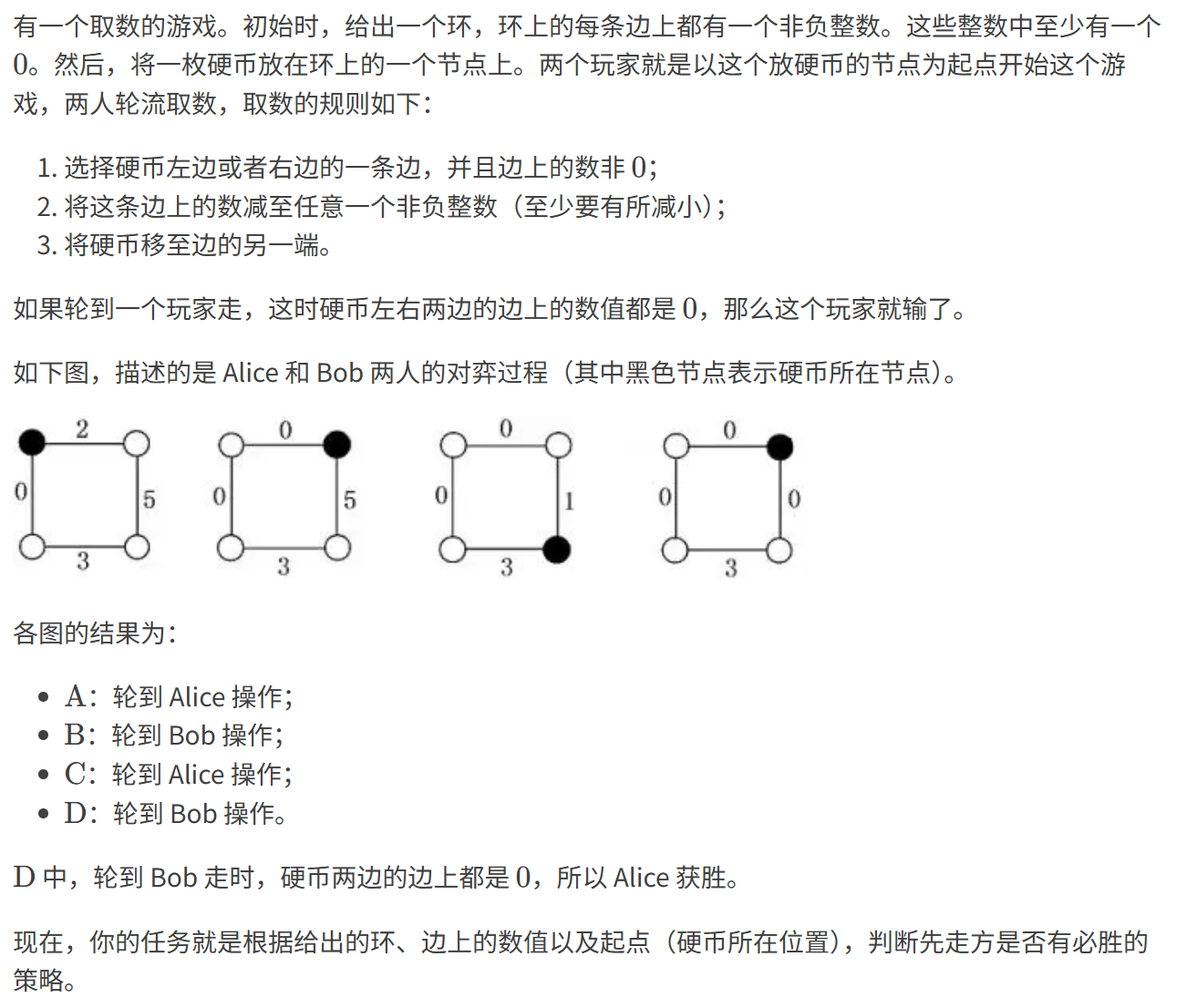
输入格式：

输出格式：

样例输入：

4
2 5 3 0

3
0 0 0

样例输出：

YES

NO

解题思路：

• 我们发现，如果先手距离某个 \(0\) 的距离为奇数，那么他只需要一路向该 \(0\) 狂奔，每次取成 \(0\) 即可获胜。

• 而如果距离均为偶数，那么无论先手如何取数，对于后手而言，其均进入了必胜态。

• 那么我们只需要考虑先手是否与某个 \(0\) 的距离为奇数即可。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 25;
int n,a[N];
inline string solve(){
	cin >> n;
	for(int i=1;i<=n;i++) cin >> a[i];
	for(int i=1;i<=n;i++){
		if(!a[i] && (i-1)&1) return "YES";
		if(!a[i]) break;
	}
	for(int i=n;i>=1;i--){
		if(!a[i] && (n-i)&1) return "YES";
		if(!a[i]) break;
	}
	return "NO";
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cout << solve();
	return 0;
}

---

P4343 [SHOI2015] 自动刷题机

• 标签：二分

• 前置知识：无

• 难度：黄 1400

题目描述：

输入格式：

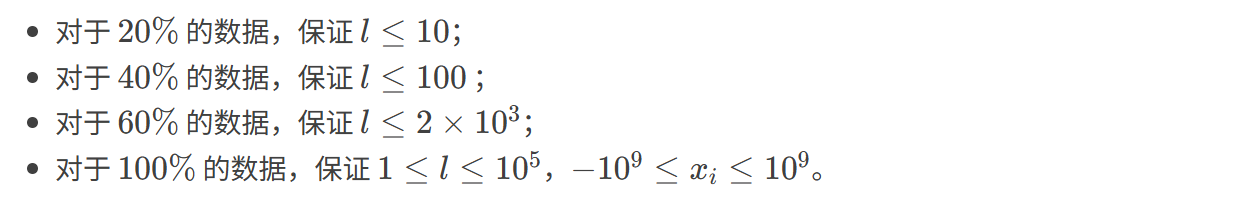
输出格式：

样例输入：

4 2
2
5
-3
9

样例输出：

3 7

解题思路：

• 我们发现对于一个给定的序列，\(n\) 越大能够通过的题数越少，具有单调性，可以对最后的 \(n\) 进行二分。

• 分别记录满足 \(\le k\) 中，等于 \(k\) 的最大值，以及 \(\ge k\) 中，等于 \(k\) 的最小值即可。

完整代码

#include<bits/stdc++.h>
#define mid (((l)+(r))>>1)
#define int long long
using namespace std;
const int N = 1e5+5;
int n,k,a[N];
inline int get(int val){
	int cnt = 0;
	for(int i=1,sum=0;i<=n;i++){
		sum = max(0ll,sum+a[i]);
		if(sum >= val) sum = 0,++cnt;
	}
	return cnt;
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n >> k;
	for(int i=1;i<=n;i++) cin >> a[i];
	int l = 1,r = 1e18,ans1 = -1,ans2 = -1;
	while(l<=r){
		int cur = get(mid);
		if(cur <= k){
			if(cur == k) ans1 = mid;
			r = mid-1;	
		}else l = mid+1;
	}
	l = 1,r = 1e18;
	while(l<=r){
		int cur = get(mid);
		if(cur >= k){
			if(cur == k) ans2 = mid;
			l = mid+1;
		}else r = mid-1;
	}
	if(ans1 == -1) cout << -1;
	else cout << ans1 << ' ' << ans2;
	return 0;
}

---

---

P4089 [USACO17DEC] The Bovine Shuffle S

• 标签：拓扑排序

• 前置知识：链式前向星

• 难度：黄 1500

题目描述：

输入格式：

输出格式：

样例输入：

4
3 2 1 3

样例输出：

3

解题思路：

• 我们发现，想要无论什么时候都有奶牛，那么必须这些奶牛在环上。

• 所以问题就转化为求有多少个奶牛在环上，我们可以拓扑排序一下，将所有非环上的点的入度减到 \(0\)，最后统计有多少个奶牛的入度非 \(0\) 即可。

完整代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
int n,ha[N],idx,in[N],a[N];
struct Edge{int to,ne;}edge[N];
inline void ins(int u,int v){
	edge[++idx] = {v,ha[u]}, ha[u] = idx;
	in[v] += 1;
}
queue<int> qu; bool vis[N];
inline void topu(){
	for(int i=1;i<=n;i++) if(!in[i]) qu.push(i),vis[i] = true;
	while(!qu.empty()){
		int u = qu.front(); qu.pop();
		for(int i=ha[u];i;i=edge[i].ne){
			int v = edge[i].to;
			if(!vis[v] && !--in[v]) qu.push(v),vis[v] = true;
		}
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n;
	for(int i=1;i<=n;i++) cin >> a[i],ins(i,a[i]);
	topu();
	int res = 0;
	for(int i=1;i<=n;i++) if(in[i]) res++;
	cout << res;
	return 0;
}

---