[每日随题10] DP - 重链剖分 - 状压DP
![[每日随题10] DP - 重链剖分 - 状压DP](https://img2024.cnblogs.com/blog/3525992/202507/3525992-20250719200727742-435290104.png)
今天可以挑战挑战
整体概述
- 难度：1600 \(\rightarrow\) 2200 \(\rightarrow\) 2600
P6005 [USACO20JAN] Time is Mooney G
-
标签：DP
-
前置知识：链式前向星
-
难度：绿 1600
题目描述：
输入格式：
输出格式：
样例输入：
3 3 1
0 10 20
1 2
2 3
3 1
样例输出：
24
解题思路：
-
发现数据范围很小，考虑可否 \(DP\)。
-
定义 \(dp_{i,j}\) 表示第 \(i\) 天到达 \(j\) 城市的最大收益，则单次更新可以暴力枚举每个节点，更新其相邻的节点，复杂度只为 \(O(M)\)。
并且发现数据给定 \(m_i\le 1000\)，则 \(T\) 不可能超过 \(1000\) 否则 \(c*T*T\) 一定大于总收益。所以总复杂度为 \(O(1000·M)\)。
完整代码
#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 1e3+5,M = 2e3+5,INF = 0x3f3f3f3f;
int n,m,c,val[N],ha[N],idx;
struct Edge{int from,to,ne;}edge[M];
inline void ins(int u,int v){
edge[++idx] = {u,v,ha[u]}, ha[u] = idx;
}
int dp[N][N];
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin >> n >> m >> c;
for(int i=1;i<=n;i++) cin >> val[i];
for(int i=1,u,v;i<=m;i++){
cin >> u >> v;
ins(u,v);
}
for(int i=0;i<N;i++) for(int j=0;j<N;j++) dp[i][j] = -INF;
dp[0][1] = 0;
int ans = 0;
for(int t=0;t<=1000;t++){
for(int u=1;u<=n;u++){
if(dp[t][u]==-INF) continue;
for(int i=ha[u];i;i=edge[i].ne){
int v = edge[i].to;
dp[t+1][v] = max(dp[t+1][v],dp[t][u]+val[v]);
}
}
ans = max(ans,dp[t][1] - c*t*t);
}
cout << ans;
return 0;
}
P10391 [蓝桥杯 2024 省 A] 零食采购
-
标签：重链剖分
-
前置知识：线段树、状态压缩
-
难度：蓝 2200
题目描述：
输入格式：
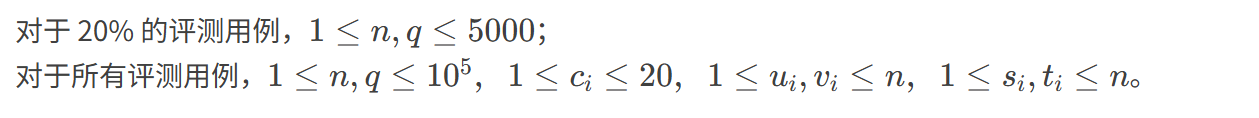
输出格式：
样例输入：
4 2
1 2 3 1
1 2
1 3
2 4
4 3
1 4
样例输出：
3
2
解题思路：
-
题目很简单，给出一棵树，每个节点有一个权值 \(1\le c\le 20\)，大量查询每次询问两个节点 \(u\)，\(v\) 在树上简单路径上经过的所有点的权值类型个数。
-
我们发现 \(c\) 很小，可以压缩到 \(int\) 的每一个位上，那么原问题转化为询问树上简单路径上的权值的 或和，那么就是裸的重链剖分的板子题了，线段树只需要支持单点修改，区间查 或和 即可。
完整代码
#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 1e5+5;
int n,q,ha[N],idx,a[N];
struct Edge{int to,ne;}edge[N<<1];
inline void ins(int u,int v){
edge[++idx]={v,ha[u]}, ha[u] = idx;
}
int fa[N],siz[N],son[N],dep[N];
inline void dfs1(int u,int par){
fa[u] = par, dep[u] = dep[par]+1;
siz[u] = 1;
for(int i=ha[u];i;i=edge[i].ne){
int v = edge[i].to;
if(v == par) continue;
dfs1(v,u), siz[u] += siz[v];
if(siz[son[u]] < siz[v]) son[u] = v;
}
}
int dfn[N],back[N],Time,top[N];
inline void dfs2(int u,int Top){
top[u] = Top;
dfn[u] = ++Time, back[Time] = u;
if(!son[u]) return;
dfs2(son[u],Top);
for(int i=ha[u];i;i=edge[i].ne){
int v = edge[i].to;
if(v != fa[u] && v != son[u]) dfs2(v,v);
}
}
#define ls ((u)<<1)
#define rs ((u)<<1|1)
#define mid (((l)+(r))>>1)
int tr[N<<2];
inline void up(int u){
tr[u] = tr[ls] | tr[rs];
}
inline void build(int l,int r,int u){
if(l == r){
tr[u] = 1<<a[back[l]];
return ;
}
build(l,mid,ls), build(mid+1,r,rs);
up(u);
}
inline int queryOR(int x,int y,int l=1,int r=n,int u=1){
if(x <= l && r <= y) return tr[u];
int ans = 0;
if(x <= mid) ans |= queryOR(x,y,l,mid,ls);
if(y > mid) ans |= queryOR(x,y,mid+1,r,rs);
return ans;
}
inline int query(int u,int v){
int ans = 0;
while(top[u] != top[v]){
if(dep[top[u]] < dep[top[v]]) swap(u,v);
ans |= queryOR(dfn[top[u]],dfn[u]);
u = fa[top[u]];
}
if(dep[u] < dep[v]) swap(u,v);
ans |= queryOR(dfn[v],dfn[u]);
return ans;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin >> n >> q;
for(int i=1;i<=n;i++) cin >> a[i];
for(int i=1,u,v;i<n;i++){
cin >> u >> v;
ins(u,v), ins(v,u);
}
dfs1(1,0);
dfs2(1,1);
build(1,n,1);
while(q--){
int u,v; cin >> u >> v;
int res = query(u,v), cnt = 0;
while(res) res &= res-1, cnt += 1;
cout << cnt << '\n';
}
return 0;
}
P7519 [省选联考 2021 A/B 卷] 滚榜
-
标签：状压DP
-
前置知识：差分数组
-
难度：紫 2600
题目描述：
输入格式：
输出格式：
样例输入：
3 6
1 2 1
6 50
4 7 9 3 0 3
11 300
6 8 8 12 0 11 6 1 0 15 5
样例输出：
5
96
30140983
解题思路：
-
发现题目的数据范围很小，求总排名方案数，肯定为状压 \(DP\)。
-
状压 \(DP\) 肯定有一维 \(O(2^n)\) 表示已经公布了哪几个人，本题的 \(b_i\) 要求单调不降，肯定需要一维 \(O(n)\) 记录上一个公布的人，需要一维 \(O(m)\) 记录已经用了多少道题。
接着考虑如何转移，对于每个状态 \(s\)，枚举由公布第 \(i\) 个人到达状态 \(s\)，再暴力枚举下一个公布的人是 \(j\)。记 \(i\) 要变成第一名所需的过题数为 \(d\)，那么由于 \(b_i\) 需要单调不降，后续所有未公布的人都需要过 \(d\) 道题，所以转移需要消耗 \(cnt*d\) 道题，其中 \(cnt\) 为还没有被公布的人数。
-
最后暴力统计所有答案即可，总复杂度 \(O(2^n·n^2·m)\)。
-
我们可以预处理数组 \(d_{i,j}\) 表示 \(i\) 超过 \(j\) 所需的最小 \(b_i\)，再预处理数组 \(s_{i}\) 表示 \(i\) 超过所有人所需的最小的 \(b_i\)，再预处理一个数组 \(cnt_i\) 表示状态为 \(i\) 时还没有公布的人数为 \(cnt_i\)，那么便可以很方便地转移了。
完整代码
#include<bits/stdc++.h>
using namespace std;
const int N = 13, M = 505;
int n,m,up,dp[1<<N][N][M],a[N],d[N][N],s[N],cnt[1<<N];
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin >> n >> m; up = 1<<n;
for(int i=0;i<n;i++) cin >> a[i];
for(int i=0;i<n;i++) for(int j=0;j<n;j++){
if(j < i) d[i][j] = max(0,a[j]-a[i]+1);
else d[i][j] = max(0,a[j]-a[i]);
}
for(int i=0;i<n;i++) for(int j=0;j<n;j++) s[i] = max(s[i],d[i][j]);
cnt[0] = n;
for(int i=1;i<up;i++) cnt[i] = cnt[i>>1] - (i&1);
for(int i=0;i<n;i++) if(n*s[i] <= m) dp[1<<i][i][n*s[i]] = 1;
for(int s=0;s<up;s++){
for(int i=0;i<n;i++) if((s>>i)&1){
for(int j=0;j<n;j++) if(!((s>>j)&1)){
for(int t=d[j][i]*cnt[s];t<=m;t++){
dp[s|(1<<j)][j][t] += dp[s][i][t-d[j][i]*cnt[s]];
}
}
}
}
long long ans = 0;
for(int i=0;i<n;i++) for(int j=1;j<=m;j++) ans += dp[up-1][i][j];
cout << ans;
return 0;
}
浙公网安备 33010602011771号