[每日随题9] 贪心 - 数学 - 并查集

整体概述

• 难度：1400 \(\rightarrow\) 1400 \(\rightarrow\) 1800

---

P7228 [COCI 2015/2016 #3] MOLEKULE

• 标签：贪心

• 前置知识：链式前向星

• 难度：黄 1400

题目描述：

输入格式：

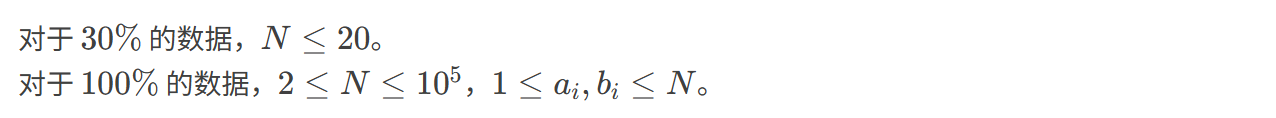
输出格式：

样例输入：

3
1 2
2 3

4
2 1
1 3
4 1

样例输出：

1
0

0
1
0

解题思路：

• 题目给定一棵树，要求将树的边添加方向，使得通路最短。

• 那么显然我们控制所有的通路长度仅为 \(1\)，我们只需要任选一个节点作根节点，第一层到第二层所有边均朝下，第二层到第三层所有边均朝上，以此类推。

• 那么把每一条边标上方向，最后输出即可。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 1e5+5;
int n,ha[N],idx = 1;
struct Edge{
	int from,to,ne;
	pair<int,int> res;
}edge[N<<1];
inline void ins(int u,int v){
	edge[++idx] = {u,v,ha[u]}, ha[u] = idx;
}
inline void dfs(int u,int par,int drt){
	for(int i=ha[u];i;i=edge[i].ne){
		int v = edge[i].to;
		if(v == par) continue;
		if(drt) edge[i].res = edge[i^1].res = {u,v};
		else edge[i].res = edge[i^1].res = {v,u};
		dfs(v,u,drt^1);
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n;
	for(int i=1,u,v;i<=n-1;i++){
		cin >> u >> v;
		ins(u,v), ins(v,u);
	}  
	dfs(1,0,1);
	for(int i=1;i<=n-1;i++) cout << (edge[i*2].res.first == edge[i*2].from) << '\n';
	return 0;
}

---

P10329 [UESTCPC 2024] Add

• 标签：数学

• 前置知识：逆元

• 难度：黄 1400

题目描述：

输入格式：

输出格式：

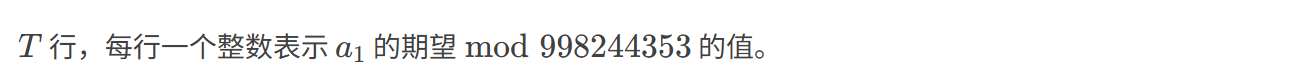
样例输入：

3
4
2
5

3
4
3
5

3
8
1
3

样例输出：

30
5
55

30
14
55

204
1
14

解题思路：

• 通过题目给出的三组样例，我们可以发现：

n : ans
1 : 1
2 : 5
3 : 14
4 : 30
5 : 55
8 : 204

• 存在着很强的规律，即 \(n=i\) 时，\(ans = 1^2 + 2^2 + 3^2 + ... + i^2\)，那么我们直接用平方和公式求和即可。

• 需要注意的是，\(\frac {n·(n+1)·(2n+1)} 6\) 中的除以 \(6\) 在模意义下需要是乘以 \(6\) 的逆元。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int mod = 998244353;
inline int qpow(int a,int b){
	int res = 1;
	for(;b;b>>=1,a=a*a%mod)
		if(b&1) res=res*a%mod;
	return res;
}
inline void solve(){
	int n; cin >> n;
	cout << n*(n+1)%mod*(2*n+1)%mod*qpow(6,mod-2)%mod << '\n';
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int T; cin >> T;
	while(T--) solve();
	return 0;
}

---

P3535 [POI 2012] TOU-Tour de Byteotia

• 标签：并查集

• 前置知识：无

• 难度：绿 1800

题目描述：

输入格式：

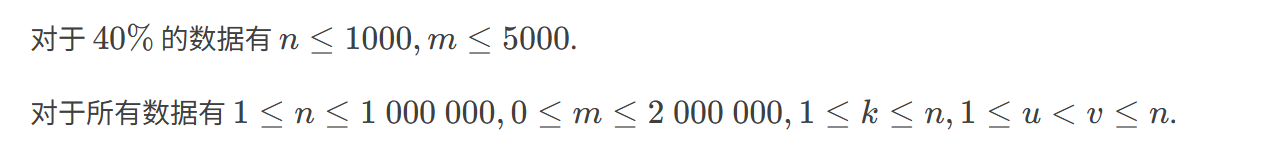
输出格式：

样例输入：

11 13 5
1 2
1 3
1 5
3 5
2 8
4 11
7 11
6 10
6 9
2 3
8 9
5 9
9 10

样例输出：

3
2 3
5 9
3 5

解题思路：

• 题目只要求编号小于等于 \(k\) 的节点不存在环上，那么若有一条边只涉及编号大于 \(k\) 的节点，直接连上该边，不可能被删除。

• 接下来问题就转化为一堆孤点，和若干个连通块之间的问题。我们把每个连通块都看成一个点，那么问题就变为最多可以连多少条边，使得图中无环。

• 显然，孤立点到每个连通块都只能连一条边，那么我们可以用并查集来维护，只有两个点不在同一个连通块内的时候才可以连边，这样就保证了最后连出来的图上无环。

• 总复杂度 \(O(m)\)。

完整代码

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+5,M = 2e6+5;
int n,m,k;
struct Edge{int u,v;}edge[M];
int fa[N],siz[N];
inline int find(int x){
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}
inline void merge(int u,int v){
	int x = find(u),y = find(v);
	if(x == y) return;
	if(siz[y] > siz[x]) siz[y] += siz[x],fa[x] = y;
	else siz[x] += siz[y],fa[y] = x; 
}
vector<Edge> res;
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n >> m >> k;
	for(int i=1;i<=n;i++) fa[i] = i,siz[i] = 1;
	for(int i=1;i<=m;i++){
		cin >> edge[i].u >> edge[i].v;	
		if(edge[i].u > k && edge[i].v > k) merge(edge[i].u,edge[i].v);
	} 
	for(int i=1;i<=m;i++){
		if(edge[i].u > k && edge[i].v > k) continue;
		if(find(edge[i].u) == find(edge[i].v))
			res.push_back({edge[i].u,edge[i].v});
		else merge(edge[i].u,edge[i].v);
	}
	cout << res.size() << '\n';
	for(auto [u,v]:res){
		if(u > v) swap(u,v);
		cout << u << ' ' << v <<'\n';
	} 
	return 0;
}