[每日随题8] 二分、贪心 - 最小生成树 - 树型DP

整体概述

• 难度：1200 \(\rightarrow\) 1400 \(\rightarrow\) 1600

---

P7305 [COCI 2018/2019 #1] Cipele

• 标签：二分、贪心

• 前置知识：贪心

• 难度：黄 1200

题目描述：

输入格式：

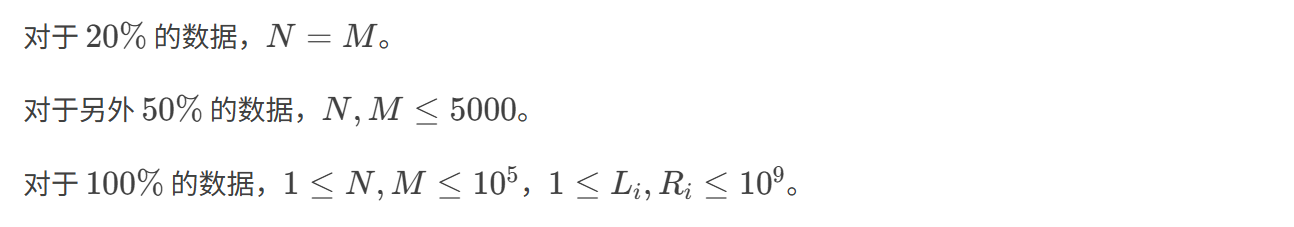
输出格式：

样例输入：

2 3
2 3
1 2 3

4 3
2 39 41 45
39 42 46

5 5
7 6 1 2 10
9 11 6 3 12

样例输出：

0

1

4

解题思路：

• 求满足情况的最小值，我们发现答案具有单调性：如果 \(x\) 满足，则所有小于 \(x\) 的答案均满足。

• 所以我们考虑对答案进行二分，求一个最小的 \(x\)，使得鞋子两两配对后，左脚和右脚大小之差的绝对值的最大值 小于等于 \(x\)。

• 考虑对于某个 \(x\) 如何 \(check\) 合法性。我们先将两个数组分别从小到大排序，那肯定会选完的那个数组来一一匹配另一个数组，不妨设为左脚数组 \(A\) 数量较少，那右脚为数组 \(B\)。

  我们发现由于排过序了，若 \(A_i\) 能匹配某个 \(B_j\) 满足 \(abs(a_i-b_j)\le x\)，那么直接匹配是最优的，对 \(A_{i+1}\) 带来的影响最小。

• 若 \(A\) 能够被匹配完，则所有小于 \(x\) 的答案均可以被满足，到更大的范围上二分答案，反之亦然。

• 总复杂度 \(O(n·log_2n)\)。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 1e5+5;
int n,m,a[N],b[N];
inline bool check(int val){
	// pa 为当前准备匹配的位置,可以从 pb 开始匹配
	for(int pa=1,pb=1;pa<=n;pa++,pb++){
		while(pb <= m && abs(b[pb] - a[pa]) > val){
			pb += 1;
		}
		if(pb > m) return false;
	}
	return true;
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n >> m;
	for(int i=1;i<=n;i++) cin >> a[i];
	for(int i=1;i<=m;i++) cin >> b[i];
	if(n > m) swap(n,m), swap(a,b);
	sort(a+1,a+n+1);
	sort(b+1,b+m+1);
	int l = 0,r = 1e5*1e9,mid;
	while(l<=r){
		mid = (l+r)>>1;
		if(check(mid)) r = mid-1;
		else l = mid+1;
	}
	cout << l;
	return 0;
}

---

P1547 [USACO05MAR] Out of Hay S

• 标签：最小生成树

• 前置知识：并查集

• 难度：黄 1400

题目描述：

输入格式：

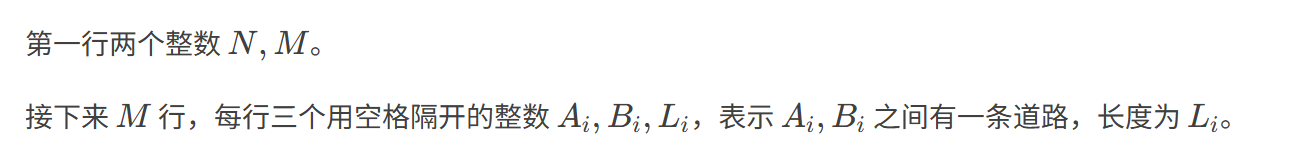
输出格式：

样例输入：

3 3
1 2 23
2 3 1000
1 3 43

样例输出：

43

解题思路：

• 一道最小生成树模板题，要求求图上最小生成树的最长边。

• 那么我们直接使用 \(kruskal\) 算法，记录最后选到的边的长度即可。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 2e3+5,M = 1e4+5;
int n,m,ha[N],idx;
struct Edge{int u,v,w;}edge[M];
int fa[N],siz[N];
inline int find(int x){
	return fa[x] == x ? x : fa[x] = find(fa[x]);
}
inline void merge(int u,int v){
	int x = find(u), y = find(v);
	if(x == y) return;
	siz[y] += siz[x], fa[x] = y;
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n >> m;
	for(int i=1;i<=n;i++) fa[i] = i,siz[i] = 1;
	for(int i=1;i<=m;i++) cin >> edge[i].u >> edge[i].v >> edge[i].w;
	sort(edge+1,edge+m+1,[&](Edge x,Edge y){return x.w < y.w;});
	for(int i=1,j=1;i<=n-1;i++,j++){
		while(find(edge[j].u) == find(edge[j].v)) j++;
		merge(edge[j].u,edge[j].v);
		if(i == n-1) cout << edge[j].w;
	}
	return 0;
}

---

P1273 有线电视网

• 标签：树型DP

• 前置知识：链式前向星，背包DP

• 难度：绿 1600

题目描述：

输入格式：

输出格式：

样例输入：

5 3
2 2 2 5 3
2 3 2 4 3
3 4 2

样例输出：

2

解题思路：

• 定义 \(dp_{u,j}\) 表示节点 \(u\) 选了 \(j\) 个叶节点的最大获益。那么我们最后要求的就是满足 \(dp_{1,j}\ge 0\) 的最大 \(j\)。

• 我们可以从叶节点向上转移。对于某个节点，每新处理完一个子树，就可以暴力枚举所有可能选出的叶节点个数，更新所有 \(dp\) 值。

• 虽然看起来是三重循环，但是由于总共只有 \(n\) 个节点，最不利情况出现在所有节点都连在 \(1\) 号节点上，此时最劣时间复杂度为 \(O(n^2)\)。

完整代码

#include<bits/stdc++.h>
#define Size(x) ((int)(x).size())
#define int long long
using namespace std;
const int N = 3e3+5,INF = 0x3f3f3f3f;
int n,m,ha[N],idx,val[N];
struct Edge{int to,ne,w;}edge[N];
inline void ins(int u,int v,int w){
	edge[++idx] = {v,ha[u],w}, ha[u] = idx;
}
int dp[N][N];
inline int dfs(int u){
	int leaf = 0;
	for(int i=ha[u];i;i=edge[i].ne){
		int v = edge[i].to, w = edge[i].w;
		int cur = dfs(v);
		for(int j=leaf+cur;j;j--)
			for(int k=1;k<=min(j,cur);k++)
				dp[u][j] = max(dp[u][j],dp[u][j-k]+dp[v][k]-w);
		leaf += cur;
	}
	if(leaf == 0){
		leaf += 1;
		dp[u][1] = val[u];
	} 
	return leaf;
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin >> n >> m;
	for(int u=1,x;u<=n-m;u++){
		cin >> x;
		for(int j=1,v,w;j<=x;j++){
			cin >> v >> w;
			ins(u,v,w);
		}
	}
	for(int u=n-m+1,x;u<=n;u++){
		cin >> x;
		val[u] += x;
	}  
	for(int i=0;i<N;i++) for(int j=0;j<N;j++) dp[i][j] = -INF;
	for(int i=1;i<=n;i++) dp[i][0] = 0;
	dfs(1);
	for(int i=n;i>=0;i--)
		if(dp[1][i] >= 0){
			cout << i;
			break;
		}
	return 0;
}

---