PTA 集训2 题解
L1-1 嫑废话上代码
-
题面:
Linux 之父 Linus Torvalds 的名言是:“Talk is cheap. Show me the code.”(嫑废话,上代码)。本题就请你直接在屏幕上输出这句话。
完整代码
#include<iostream> using namespace std; int main(){ cout << "Talk is cheap. Show me the code."; return 0; }
L1-2 九牛一毛
-
题面:
这是一道脑筋急转弯题:猪肉一斤 15 元,鸡肉一斤 20 元,那么一毛钱能买多少头牛?
答案是:9 —— 因为“九牛一毛”。
本题就请你按照这个逻辑,计算一下 N 块钱能买多少斤猪肉、多少斤鸡肉、多少头牛。
输入格式:
输入在一行中给出一个不超过 1000 的正整数 N,即以“元”为单位的货币量。
输出格式:
在一行中顺序输出 N 块钱能买多少斤猪肉、多少斤鸡肉、多少头牛。三个数字都只取整数部分,其间以 1 个空格分隔,行首尾不得有多余空格。
-
解题思路:
要求分别计算,N 块钱能买多少猪肉、鸡肉和牛肉且只取整数部分,前两个直接分别整除 15 和 20,牛 用 一毛钱可以买 9 只,输入的 N 单位是元,换算一下即可。
完整代码
#include<iostream> using namespace std; int main(){ int n; cin >> n; printf("%d %d %d",n/15,n/20,n*10*9); return 0; }
L1-3 小孩子才做选择,大人全都要
-
题面:
阿汪面前有两只盲盒,每只盒子打开都有两种可能:或者装了 X 克狗粮,或者是一只容量为 Y 克的狗粮储蓄盒。如果是狗粮,阿汪可以快乐地吃掉;如果是空储蓄盒,那就倒霉了,阿汪必须想办法找到狗粮把这只储蓄盒装满,自己还吃不到。
正当阿汪发愁不知道该怎么选的时候,铲屎官大手一挥:“小孩子才做选择,大人全都要!”但全都要的结果,却不一定是赚了还是亏了……
我们假设聪明的阿汪总是能嗅出狗粮最多的盒子,并且绝不会选任何储蓄盒。而铲屎官没有这样的鼻子,他一定是全都要。铲屎官如果打开了有储蓄盒的盒子,就必须想办法把储蓄盒装满,他会优先用另一只盒子里的狗粮装(如果另外一只盒子里有狗粮),不够了还得自己去买新的狗粮,这样阿汪可就亏啦,什么都吃不到了。本题就请你判断阿汪到底是赚了还是亏了。
-
题意分析:
可以理解成有两个数字 a,b,阿汪只会选其中最大的那个数。但若都是负数就不选,此时总和算作 0 。
铲屎官直接将两个数字相加。若 a+b 小于 0,则也算作总和为 0 。
最后判断 阿汪 算出来的数字 与 铲屎官 算的数字的大小关系,输出对应的表情即可。
完整代码
#include<iostream> using namespace std; int main(){ int a,b; cin >> a >> b; int chose1 = max(max(a,b),0); // 阿汪的选择 int chose2 = max(a+b,0); // 铲屎官的总和 printf("%d %d\n",chose1,chose2); if(chose1 > chose2) printf("T_T"); else if(chose1 == chose2) printf("-_-"); else printf("^_^"); return 0; }
L1-4 拯救外星人
-
题面:
你的外星人朋友不认得地球上的加减乘除符号,但是会算阶乘 —— 正整数 N 的阶乘记为 “N!”,是从 1 到 N 的连乘积。所以当他不知道“5+7”等于多少时,如果你告诉他等于“12!”,他就写出了“479001600”这个答案。
本题就请你写程序模仿外星人的行为。
输入在一行中给出两个正整数 A 和 B。
在一行中输出 (A+B) 的阶乘。题目保证 (A+B) 的值小于 12。
-
解题思路:
题目只要求计算 (A+B)! 的值,且 (A+B)<12 即阶乘值在 int 的范围内。
那么直接一个循环从 1 乘到 (A+B) 即可
完整代码
#include<iostream> using namespace std; int main(){ int a,b; cin >> a >> b; int n = a+b, res = 1; for(int i=1;i<=n;i++) res *= i; printf("%d",res); return 0; }
L1-5 试试手气
-
题面:
我们知道一个骰子有 6 个面,分别刻了 1 到 6 个点。下面给你 6 个骰子的初始状态,即它们朝上一面的点数,让你一把抓起摇出另一套结果。假设你摇骰子的手段特别精妙,每次摇出的结果都满足以下两个条件:
1、每个骰子摇出的点数都跟它之前任何一次出现的点数不同;
2、在满足条件 1 的前提下,每次都能让每个骰子得到可能得到的最大点数。
那么你应该可以预知自己第 n 次(1≤n≤5)摇出的结果。
输入格式:
输入第一行给出 6 个骰子的初始点数,即 [1,6] 之间的整数,数字间以空格分隔;第二行给出摇的次数 n(1≤n≤5)。
输出格式:
在一行中顺序列出第 n 次摇出的每个骰子的点数。数字间必须以 1 个空格分隔,行首位不得有多余空格。
-
解题思路:
由于骰子每次都会骰 一个未出现过的最大点数,即一定是 \({6,5,4,3,2,1}\) 这样依次骰出。
我们先忽略骰子给定的初始状态,此时若要猜测第 \(2\) 次骰出的值,那便全部都是 \(5\),猜测第 \(4\) 次骰出的值 ,那便全部都是 \(3\),即第 \(n\) 次骰出的结果为 \(6-n+1\)。
那么初始状态会对结果有什么影响呢?假如初始状态为 5,要猜第 3 次的结果。
第一次骰出 6,第二次本来可以骰 \(5\) 的,由于 5 初始状态出现过了,现在只能是 \(4\) 了,然后第三次骰出 3 。
那么我们可以轻易地得出结论,如果第 n 次骰出的结果,小于等于初始状态,证明需要跳过一次初始状态,骰出的结果就为 \(6-n+1-1 = 6-n\),否则骰出的结果就为 \(6-n+1\) .
完整代码
#include<iostream> using namespace std; int a[6]; int main(){ for(int i=0;i<6;i++) scanf("%d",&a[i]); int n; scanf("%d",&n); for(int i=0;i<6;i++){ if(i) printf(" "); printf("%d",(6-n+1 <= a[i]) ? (6-n) : (6-n+1)); } return 0; }
L1-6 打PTA
-
题面:
传说这是集美大学的学生对话。本题要求你做一个简单的自动问答机,对任何一个问句,只要其中包含 PTA 就回答 Yes!,其他一概回答 No.。
对每一行句子,如果其结尾字符为问号 ? 则判断此句中有无 PTA?如果有则在一行中输出 Yes!,否则输出 No.。如果不是问号结尾,则敷衍地回答 enen。
-
解题思路:
直接读入一整行数据到字符串 str 中,先判断末尾是否为
?,不是的话直接输出enen结束。否则接着用
str.find("PTA")寻找字符串中PTA出现的位置,如果返回值为-1代表没有出现过,则输出No.,否则输出Yes!即可。完整代码
#include<iostream> using namespace std; int main(){ int T; cin >> T; getchar(); // 注意第一行输入末尾的回车会 使getline()函数误读入,这里需要额外用 getchar() 读掉 while(T--){ string str; getline(cin,str); if(str[str.size()-1]!='?') cout << "enen\n"; // 判断末尾不为问号 else if(str.find("PTA")!=-1) cout << "Yes!\n"; //出现过 "PTA" else cout << "No.\n"; // 未出现过 } return 0; }
L1-7 机工士姆斯塔迪奥
-
题面:
你需要处理这个副本其中的一个机制:N×M 大小的地图被拆分为了 N×M 个 1×1 的格子,BOSS 会选择若干行或/及若干列释放技能,玩家不能站在释放技能的方格上,否则就会被击中而失败。
给定 BOSS 所有释放技能的行或列信息,请你计算出最后有多少个格子是安全的。
输入格式:
输入第一行是三个整数 \(N,M,Q\) 表示地图为 \(N\) 行 \(M\) 列大小以及选择的行/列数量。($ 1≤N×M≤10^5 ,0≤Q≤1000$ )
接下来 Q 行,每行两个数 \(T_i,C_i\),其中 \(T_i=0\) 表示 BOSS 选择的是一整行,\(T_i=1\) 表示选择的是一整列,\(C_i\) 为选择的行号/列号。行和列的编号均从 \(1\) 开始。
输出格式:
输出一个数,表示安全格子的数量。
-
解题思路:
首先关注数据范围,行数 N 和列数 M 都很大到了 1e5 的范围,开不出二维数组进行暴力模拟。那么我们可以开两个 bool 数组 row 和 line,分别记录下 boss 对哪些行 和 哪些列 进行了攻击。
若第 \(i\) 行被攻击,\(row[i] = 1\),若第 \(j\) 列被攻击,\(line[j] = 1\)
最后我们只需要统计分别有 多少行 和 多少列 被攻击,即
row[i] == 1和row[j] == 1的数量分别为cntr和cntl,那么安全格的数量就为(n-cntr)*(m-cntl),如图: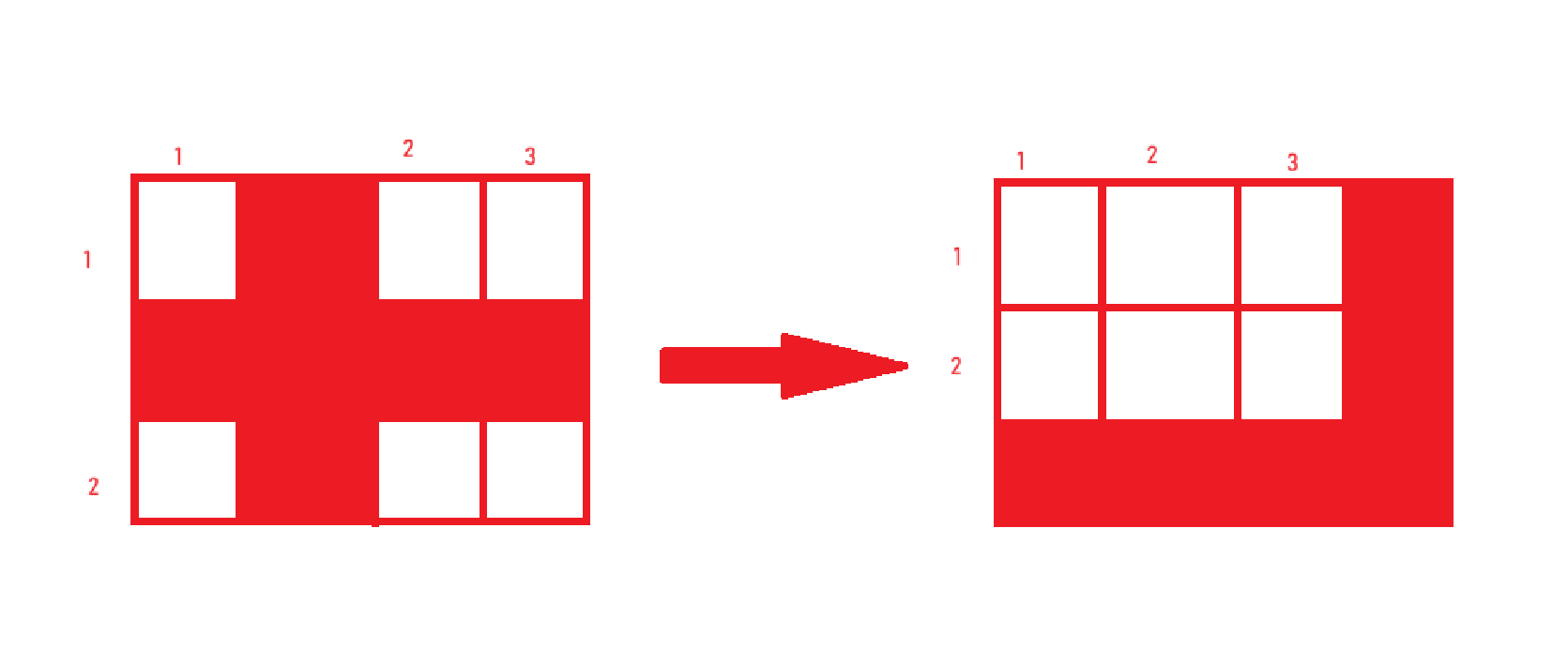
完整代码
#include<iostream> using namespace std; const int N = 1e5+5; bool row[N],line[N]; int main(){ int n,m,q; cin >> n >> m >> q; while(q--){ int op,x; cin >> op >> x; if(!op) row[x] = true; else line[x] = true; } int cnta = 0, cntb = 0; for(int i=0;i<N;i++) if(row[i]) cnta++; for(int i=0;i<N;i++) if(line[i]) cntb++; printf("%d",(n-cnta)*(m-cntb)); return 0; }
L1-8 随机输一次
-
题面:
现要求你编写一个控制赢面的程序,根据对方的出招,给出对应的赢招。但是!为了不让对方意识到你在控制结果,你需要隔 \(K\) 次输一次,其中 \(K\) 是系统设定的随机数。
输入首先在第一行给出正整数 \(N\)(\(≤10\)),随后给出 \(N\) 个系统产生的不超过 \(10\) 的正随机数 \({ K_1,K_2,⋯,K_N}\),数字间以空格分隔。这意味着第 \(i\)(\(i=0,1,⋯,N−1\))次输局之后应该隔 \(K_{i+1}\) 次再让下一个输局。
如果对方出招太多,则随机数按顺序循环使用。例如在样例中,系统产生了 3 个随机数 {2, 4, 1},则你需要:赢 2 次,输 1 次;赢 4 次,输 1 次;赢 1 次,输 1 次;然后再次回到第 1 个随机数,赢 2 次,输 1 次。
之后每行给出对方的一次出招:
ChuiZi代表 “锤子”、JianDao代表“剪刀”、Bu代表“布”。End代表输入结束,这一行不要作为出招处理。输入保证对方至少出了一招。 -
解题思路:
我们用变量
times记录已经赢了几次;用数组 \(a[\space]\) 记录依次要赢几局再输;用一个变量 \(p\) 表示若当前赢了 \(a[p]\) 局就需要输一局。用
win和los两个unordered_map分别来记录 什么能赢 锤石、剪刀、布,和什么能 输给 锤子、剪刀、布。然后依次处理每行数据,若当前不需要输,就根据
win来输出什么能赢对手,然后times++。若需要输了,就根据los输出怎么输对手,然后times=0,p=(p+1)%n来更新要输给对手的次数。完整代码
#include<iostream> #include<unordered_map> using namespace std; const int N = 15; unordered_map<string,string> win,los; int a[N]; int main(){ win["ChuiZi"] = "Bu"; win["Bu"] = "JianDao"; win["JianDao"] = "ChuiZi"; // 用布赢锤子,剪刀赢布,锤子赢剪刀 los["ChuiZi"] = "JianDao"; los["Bu"] = "ChuiZi"; los["JianDao"] = "Bu"; // 用剪刀输给锤子,锤子输给布,布输给剪刀 int n; cin >> n; for(int i=0;i<n;i++) cin >> a[i]; getchar(); string op; cin >> op; int times = 0,p = 0; while(op != "End"){ if(times == a[p]){ // 需要输了 times = 0; p = (p+1)%n; // 依题意,循环使用输的次数的数组 cout << los[op] << '\n'; }else{ ++times; // 这局要赢 cout << win[op] << '\n'; } cin >> op; } return 0; }
L2-1 插松枝
-
题面:
人造松枝加工场的工人需要将各种尺寸的塑料松针插到松枝干上,做成大大小小的松枝。他们的工作流程(并不)是这样的:
每人手边有一只小盒子,初始状态为空。
每人面前有用不完的松枝干和一个推送器,每次推送一片随机型号的松针片。
工人首先捡起一根空的松枝干,从小盒子里摸出最上面的一片松针 —— 如果小盒子是空的,就从推送器上取一片松针。将这片松针插到枝干的最下面。
工人在插后面的松针时,需要保证,每一步插到一根非空松枝干上的松针片,不能比前一步插上的松针片大。如果小盒子中最上面的松针满足要求,就取之插好;否则去推送器上取一片。如果推送器上拿到的仍然不满足要求,就把拿到的这片堆放到小盒子里,继续去推送器上取下一片。注意这里假设小盒子里的松针片是按放入的顺序堆叠起来的,工人每次只能取出最上面(即最后放入)的一片。
当下列三种情况之一发生时,工人会结束手里的松枝制作,开始做下一个:
(1)小盒子已经满了,但推送器上取到的松针仍然不满足要求。此时将手中的松枝放到成品篮里,推送器上取到的松针压回推送器,开始下一根松枝的制作。
(2)小盒子中最上面的松针不满足要求,但推送器上已经没有松针了。此时将手中的松枝放到成品篮里,开始下一根松枝的制作。
(3)手中的松枝干上已经插满了松针,将之放到成品篮里,开始下一根松枝的制作。
现在给定推送器上顺序传过来的 N 片松针的大小,以及小盒子和松枝的容量,请你编写程序自动列出每根成品松枝的信息。
-
解题思路:
模拟工人插松枝的过程。用 栈 模拟小盒子。用一个变量
last记录当前松枝最上方的松针大小。用一个变量has来记录当前松枝上插了 几个松针。我们会发现,工人每次需要先检查 小盒子顶部 的 松针大小,若 小于等于
last,那么从小盒子的顶端取出。直到 当小盒子顶端的大小 大于
last或者 小盒子空了 或者 松枝被插满了 的时候,才会停止考虑小盒子内的松针。此时如果
has == k即这个松枝被插满了,或者 传送带上没有松针了,或者 传送带上的松针大小 大于last且小盒子已经满了装不进去 的时候,结束这个松枝的制作,has 清空为 0 。否则此时 has 一定小于 k,并且 要么传送带上的松针小于等于
last,要么松针大于last且盒子装的进去。对于前者,我们将其插到松针上;对于后者,我们装进小盒子里。
然后循环,直到传送带和小盒子均为空时 结束。
我们可以当一个松针被插上松枝的时候直接将其输出出来,这样就不用考虑记录下他们了。当一个松枝结束制作的时候,直接输出一个回车。
完整代码
#include<iostream> #include<stack> using namespace std; const int N = 1e3+5,INF = 0x7fffffff; int n,m,k,a[N]; stack<int> bask; // 用栈模拟篮子 int main(){ scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=n;i++) scanf("%d",&a[i]); int last = INF,has = 0,pos = 1; // 松枝顶端的大小 初始无穷大,已经插上的数量,传送带上第几个松针 while(!bask.empty() || pos<=n){ // 篮子不空且传送带不空 即还有松针 while(!bask.empty() && bask.top()<=last && has<k){ //一直从篮子里取,直到取不了为止 if(has) printf(" "); printf("%d",bask.top()); // 每插上一个松针直接输出 ++has,last = bask.top(),bask.pop(); // 更新当前松枝最顶端的大小 } // 运行到这里,要么松枝被插满了,要么篮子里的松针全部不符合要求 // 那么如果 松枝被插满 或 传送带空了 或 (传送带上的也不符合要求 但 放不进篮子) 的时候,结束这个松枝的制作 if(has == k || pos > n || (a[pos] > last && bask.size() == m)){ printf("\n"); // 结束制作的时候直接输出回车 has = 0,last = INF; // 重置 has 和 last continue; } // 运行到这里,要么传送带上的松针符合要求,要么不符合要求但是可以放进篮子里 if(a[pos] > last) bask.push(a[pos]),++pos; // 不符合要求放进篮子里 else{ if(has) printf(" "); printf("%d",a[pos]); // 符合要求就插上,然后直接输出 ++has,last = a[pos++]; // 更新当前松枝最顶端的大小 } } return 0; }
L2-2 老板的作息表
-
题面:
本题就请你编写程序,检查任意一张时间表,找出其中没写出来的时间段。
输入格式:
输入第一行给出一个正整数 N,为作息表上列出的时间段的个数。随后 N 行,每行给出一个时间段,格式为:
hh:mm:ss - hh:mm:ss其中 hh、mm、ss 分别是两位数表示的小时、分钟、秒。第一个时间是开始时间,第二个是结束时间。题目保证所有时间都在一天之内(即从 00:00:00 到 23:59:59);每个区间间隔至少 1 秒;并且任意两个给出的时间区间最多只在一个端点有重合,没有区间重叠的情况。
输出格式:
按照时间顺序列出时间表中没有出现的区间,每个区间占一行,格式与输入相同。题目保证至少存在一个区间需要输出。
-
解题思路:
首先为了方便处理将所有时间的单位转化为秒,即
t = h*3600 + m*60 + s首先有一个朴素思想:用一个 bool 数组 vis 将所有出现过的时间段标记,最后检查没有被标记过的时间段,作为输出。
比如有数据输入
00:00:00 - 00:00:02那么将数组的 \(vis[0]~vis[2]\) 标记为 \(1\),输出的时候发现00:00:03 - 23:59:59这个时间段没有被标记过,那么输出00:00:03 - 23:59:59但或许你已经发现了,这个办法没法输出端点值。比如刚才理论上应该输出
00:00:02 - 23:59:59的,该如何解决呢?我们可以修改一下输出,假如输入为
00:00:00 - 00:00:01和00:00:04 - 23:59:59,此时只有 \(vis[2]\) 和 \(vis[3]\) 是 \(0\),那么我们输出 \((2-1)\) ~ \((3+1)\) 即00:00:01 - 00:00:04就没有问题了。但是我们会发现有一些问题: 左边界 \(0\) 和 右边界 \(23:59:59\) 会让我们输出两个越界的时间,那么特判一下这两个时间点即可。更严重的是 比如
00:00:00 - 00:00:01和00:00:02 - 23:59:59,这时候理论上应该要输出00:00:01 - 00:00:02,但是在我们的标记数组中却全部都是 1,导致没有输出。解决方法是,将所有时间都翻倍,即 \(vis[0]\) 和 \(vis[1]\) 都表示
00:00:00,并且标记[l,r]为 \(1\) 的时候改为标记[l*2,r*2]为 1 。这样我们会发现,对于刚才的那个数据,\(vis[3]\) 仍然会等于 \(0\),这是因为
[00:00:00,00:00:01]时标记了[00:00:00,00:00:02]为 \(1\),[00:00:02,23:59:59]的时候标记了[00:00:04,23:59:59 *2]为 \(1\) 。而中间的 \(vis[3]\) 若想要被标记,一定是有某个区间包含了00:00:02,这样就不会有未被覆盖的区间被我们漏掉了。接着考虑如何通过 \(vis[3] = 0\) 来输出
00:00:01 - 00:00:02,我们可以发现3/2 = 1,3/2 + 1 = 2,那么输出的问题也解决了。最后考虑如何找到一个连续的全为 \(0\) 的区间,我们沿时间轴从左向右遍历,若
vis[i-1] == 1 && vis[i] == 0,那么 \(i\) 就是这个连续全为 \(0\) 的区间的左端点。若vis[i-1] == 0 && vis[i] == 1那么 \(i-1\) 就是这个连续全为 \(0\) 的区间的右端点。为了使
00:00:00和23:59:59这两个边界可以被识别,我们将整个时间段的两侧都用 1 包起来。但此时由于下标为 \(i=0\) 时 \(i-1 = -1\) 会越界,那我们再将所有的下标整体加 \(1\) 。这样从 \(1\) 遍历到 \(23:59:59 *2 +1\) 即可。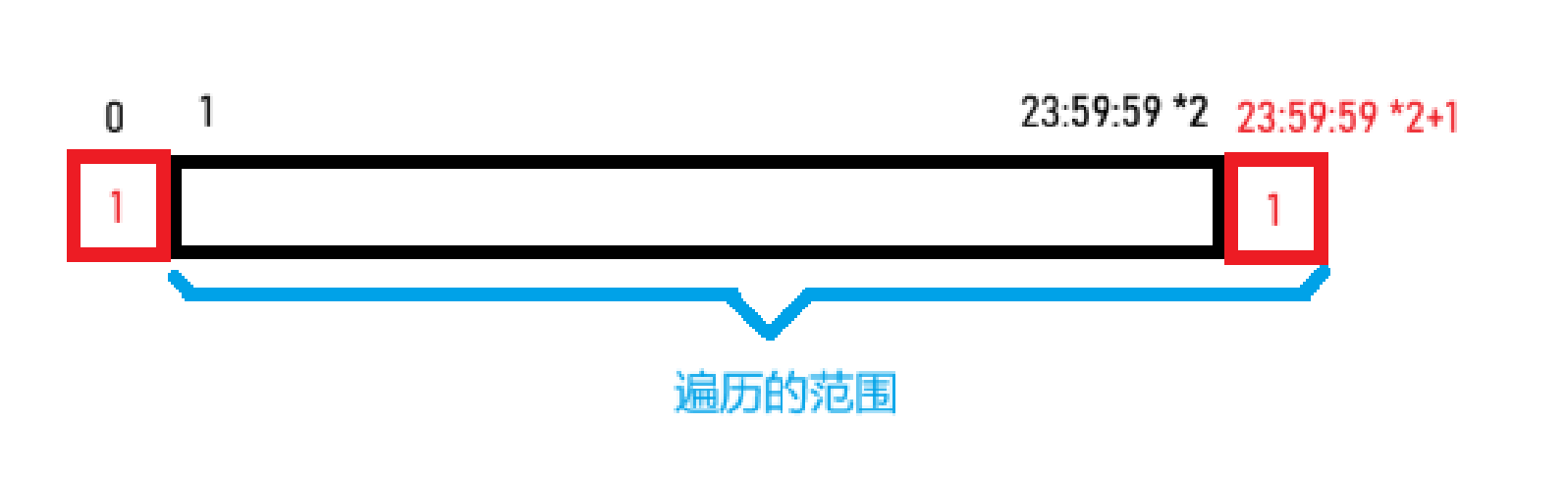
至此问题完美解决,我们甚至可以遇到一个左端点就输出,遇到一个右端点就输出。
完整代码
#include<iostream> #define T(a,b,c) (((((a)*3600)+((b)*60)+c))*2+1) // 转化单位为 秒 后,乘 2 再 +1 #define h(T) (((T-1)/2)/3600) // 求小时前 先 -1 再 /2 #define m(T) ((((T-1)/2)%3600)/60) #define s(T) (((T-1)/2)%60) using namespace std; const int N = 60*60*24*2+5, M = T(23,59,59)+1; // M 为遍历的右边界 bool vis[N]; int main(){ int n; scanf("%d",&n); for(int i=1;i<=n;i++){ int h1,m1,s1,h2,m2,s2; scanf("%d:%d:%d - %d:%d:%d",&h1,&m1,&s1,&h2,&m2,&s2); for(int l = T(h1,m1,s1),r = T(h2,m2,s2);l<=r;l++) vis[l] = true; // 出现的时间范围全部设置为 true } vis[0] = vis[M] = 1; // 将整个时间段用 1 包起来 for(int i=1;i<=M;i++){ if(vis[i-1] && !vis[i]) printf("%02d:%02d:%02d",h(i),m(i),s(i)); // 遇到左端点就输出 else if(!vis[i-1] && vis[i]) printf(" - %02d:%02d:%02d\n",h(i),m(i),s(i)); //遇到右端点就输出 } return 0; }
L2-3 智能护理中心统计
-
题面:
智能护理中心系统将辖下的护理点分属若干个大区,例如华东区、华北区等;每个大区又分若干个省来进行管理;省又分市,等等。我们将所有这些有管理或护理功能的单位称为“管理结点”。现在已知每位老人由唯一的一个管理结点负责,每个管理结点属于唯一的上级管理结点管辖。你需要实现一个功能,来统计任何一个管理结点所负责照看的老人的数量。
注意这是一个动态问题,即随时可能有老人加入某个管理结点,并且老人是有可能从一个管理结点换到另一个管理结点去的。
输入格式:
输入在第一行中给出 \(2\) 个正整数:\(N\)(\(≤10^4\))是老人的总数量,即老人们从 \(1\) 到 \(N\) 编号;\(M\)(\(≤10^5\))是归属关系的总数。
接下来是 \(M\) 行,每行给出一对归属关系,格式为:
A B表示 \(A\) 归属于 \(B\)。\(A\) 或 \(B\) 如果是某个管理结点,则用不超过 \(4\) 个大写英文字母表示其名称;如果是某位老人,则用老人的编号表示。这里每个 \(A\) 保证只有唯一的上级归属 \(B\),且只有这个中心系统本身是没有上级归属的。此外,输入保证没有老人自己承担管理结点的角色,即 \(B\) 一定是一个管理结点,不可能是老人的编号。但一个管理结点既可以管辖下级结点,也可以直接护理一部分老人。
随后每行给出一个指令,格式为:
指令 内容如果 指令 为
T,则表示有老人要入院或转院,内容是某老人的编号和要去的管理结点的名称,以空格分隔;如果 指令 为Q,则内容是一个管理结点的名称,意思是统计这个结点所负责照看的老人的数量;如果 指令 为E,则表示输入结束。题目保证指令总数不会超过 \(100\) 个。输出格式
对每个
T指令,将对应的老人转存到对应的管理结点名下;对每个Q指令,在一行中输出对应管理结点所负责照看的老人的数量。读到E指令就结束程序。 -
解题思路:
我们可以把每个 管理节点 都看成树上的一个节点,每个管理节点有自己的一个 siz 值,记录这个管理节点 管理着 多少个老人。
那么我们可以根据题意建出一棵树,
Q操作就是查询树上某个节点,求以该节点为根的子树上的所有 siz 值之和。由于某个老人同一时间只会属于一个 管理节点,那么我们将其记录下来,在
T操作的时候将原先管理节点的 siz-1,将更新后的管理节点的 siz+1 即可。由于数据输入的时候,每个管理节点输入的是其名字,我们需要人为使用
unordered_map将其编号成数字,方便后续树上操作。同时由于不好分辨一行内输入的是 字符串 还是 老人的数字编号,我们都当做是字符串来读入,然后使用
isdigit()函数来判断第一个字符是不是数字,若是数字则代表这行命令的含义是 某个老人 属于 某个 管理节点,若不是则代表含义是 管理节点 \(u\) 的父节点是 管理节点 \(v\)。本题我使用的建图方法是:链式前向星 建图,在很多情况下比 邻接矩阵 和 邻接表 好用。
完整代码
#include<iostream> #include<unordered_map> using namespace std; const int N = 1e5+5; int ha[N],idx,siz[N]; // siz 记录该管理节点 管多少个老人 struct Edge{int from,to,ne;}edge[N]; inline void ins(int u,int v){ // 链式前向星建图 edge[++idx].from = u,edge[idx].to = v; edge[idx].ne = ha[u],ha[u] = idx; } unordered_map<string,int> id; // 将每个管理节点 编号 unordered_map<string,int> owner; // 记录每个老人 所属的管理节点的编号 int n,m,cnt; inline int query(int u){ // 求以 u 为根的子树上所有节点的 cnt值 之和 int res = siz[u]; // 自己 for(int i=ha[u];i;i=edge[i].ne) res += query(edge[i].to); // 所有孩子 return res; } int main(){ cin >> n >> m; for(int i=1;i<=m;i++){ string u,v; cin >> u >> v; if(id.find(v) == id.end()) id[v] = ++cnt; // 为每个管理节点编号 if(isdigit(u[0])) owner[u] = id[v], ++siz[id[v]]; // 如果 u 是数字, 代表该行数据表示 老人 u 属于节点 v, 记录该信息并将 siz[v]+1 else{ if(id.find(u) == id.end()) id[u] = ++cnt; // 为管理节点编号 ins(id[v],id[u]); // 连一条 v->u 的边 } } char op; cin >> op; while(op != 'E'){ string a,b; if(op == 'Q'){ cin >> a; cout << query(id[a]) << '\n'; // 查询 管理节点a 为根的子树上所有节点的 cnt 值之和 }else{ cin >> a >> b; --siz[owner[a]], ++siz[id[b]]; // 将老人所属的原管理节点 siz-1, 新管理节点 siz+1 owner[a] = id[b]; // 更新老人所属的节点 } cin >> op; } return 0; }
L2-4 大众情人
-
题面:
人与人之间总有一点距离感。我们假定两个人之间的亲密程度跟他们之间的距离感成反比,并且距离感是单向的。例如小蓝对小红患了单相思,从小蓝的眼中看去,他和小红之间的距离为 1,只差一层窗户纸;但在小红的眼里,她和小蓝之间的距离为 108000,差了十万八千里…… 另外,我们进一步假定,距离感在认识的人之间是可传递的。
例如小绿觉得自己跟小蓝之间的距离为 2,则即使小绿并不直接认识小红,我们也默认小绿早晚会认识小红,并且因为跟小蓝很亲近的关系,小绿会觉得自己跟小红之间的距离为 1+2=3。当然这带来一个问题,如果小绿本来也认识小红,或者他通过其他人也能认识小红,但通过不同渠道推导出来的距离感不一样,该怎么算呢?我们在这里做个简单定义,就将小绿对小红的距离感定义为所有推导出来的距离感的最小值。
一个人的异性缘不是由最喜欢他/她的那个异性决定的,而是由对他/她最无感的那个异性决定的。我们记一个人 i 在一个异性 j 眼中的距离感为 \(D_{ij}\),将 \(i\) 的“异性缘”定义为 \(1/max\){\(D_{i,j}\) }$ ,j∈S(i)$,其中 \(S(i)\) 是相对于 \(i\) 的所有异性的集合。那么“大众情人”就是异性缘最好(值最大)的那个人。
本题就请你从给定的一批人与人之间的距离感中分别找出两个性别中的“大众情人”。
输入格式:
输入在第一行中给出一个正整数 \(N\)(\(≤500\)),为总人数。于是我们默认所有人从 \(1\) 到 \(N\) 编号。
随后 \(N\) 行,第 \(i\) 行描述了编号为 \(i\) 的人与其他人的关系,格式为:
性别 K 朋友1:距离1 朋友2:距离2 …… 朋友K:距离K其中
性别是这个人的性别,F表示女性,M表示男性;K(\(<N\) 的非负整数)为这个人直接认识的朋友数;随后给出的是这K个朋友的编号、以及这个人对该朋友的距离感。距离感是不超过 \(10^ 6\) 的正整数。题目保证给出的关系中一定两种性别的人都有,不会出现重复给出的关系,并且每个人的朋友中都不包含自己。
输出格式:
第一行给出自身为女性的“大众情人”的编号,第二行给出自身为男性的“大众情人”的编号。如果存在并列,则按编号递增的顺序输出所有。数字间以一个空格分隔,行首尾不得有多余空格。
-
解题思路:
题目中 A 对 B 该朋友的距离感为 w,可以看作节点 A 到节点 B 有一条长为 w 的有向边,则题目规定 A 对 B 的距离感为节点 A 到节点 B 的最短距离。
由于一个人 A 的 异性缘的倒数 为其他所有人到 A 的最短路径中取最大值,所以我们需要求任意两点间的最短路径。那么多源最短路我们考虑使用 Floyd 算法,可以在 \(n^3\) 的时间复杂度内求得。由于 \(n\) 只有 \(500\), \(n^3 = 1.25\times 10^6\) 并不会超时。
那么我们可以用一个 二维数组 \(dist\),\(dist[i][j] = w\) 表示第 \(i\) 个到第 \(j\) 个人的最短距离为 \(w\)。
然后对于一个人 \(i\),若其性别是
M,则对于所有性别为F的人 \(j\),取 \(dist[j][i]\) 中的最大值,即为 \(i\) 的 异性缘的倒数 记为mx[i]。同理若其性别是F,则对于所有性别为M的人 \(j\),取 \(dist[j][i]\) 中的最大值作为其mx[i]。最后每种性别的异性缘最大值 为该性别所有人
mx[i]中的最小值,分别记为mnf和mnm。然后按要求分别输出性别
F中mx[i]值为mnf与性别M中mx[i]mnm的人的编号即可。完整代码
#include<iostream> using namespace std; const int N = 505,INF = 0x7fffffff; int n,dist[N][N],mx[N]; bool sex[N]; // dist[i][j] 为 i 到 j 的最短路径, sex[i] 为 i 的性别 int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) dist[i][j] = INF; // 初始值距离设为无穷大 for(int u=1;u<=n;u++){ char ch; int k; getchar(); scanf("%c %d",&ch,&k); sex[u] = (ch=='M') ? 0 : 1; for(int i=1,v,w;i<=k;i++) scanf("%d:%d",&v,&w),dist[u][v] = w; } for(int k=1;k<=n;k++) // 三重循环 Floyd 算法求任意两点间最短路 for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){ if(i == j) continue; //若两个都是 INF,相加后会int溢出,转为 long long 类型后再相加,1ll * a 就会使 a 变成 long long 类型 dist[i][j] = min(1ll*dist[i][j],1ll*dist[i][k] + dist[k][j]); } int mnf = INF,mnm = INF; // mnf 为 性别F 中的最小的 mx[i]值, mnm 为 性别M 中的最小的 mx[i]值 for(int i=1;i<=n;i++){ mx[i] = -INF; for(int j=1;j<=n;j++) if(sex[i] ^ sex[j]) mx[i] = max(dist[j][i],mx[i]); // 只考虑异性 if(sex[i] == 0) mnm = min(mnm,mx[i]); // 更新对应性别的 mn 值 else mnf = min(mnf,mx[i]); } for(int i=1,cnt=0;i<=n;i++) if(sex[i] && mx[i]==mnf){ // 输出性别 F 所有 mx[i] 为 mnf 的人的编号 if(cnt) printf(" "); ++cnt; printf("%d",i); } printf("\n"); for(int i=1,cnt=0;i<=n;i++) if(!sex[i] && mx[i]==mnm){ // 输出性别 M 所有 mx[i] 为 mnm 的人的编号 if(cnt) printf(" "); ++cnt; printf("%d",i); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号