Luogu SP1716 GSS3 - Can you answer these queries III

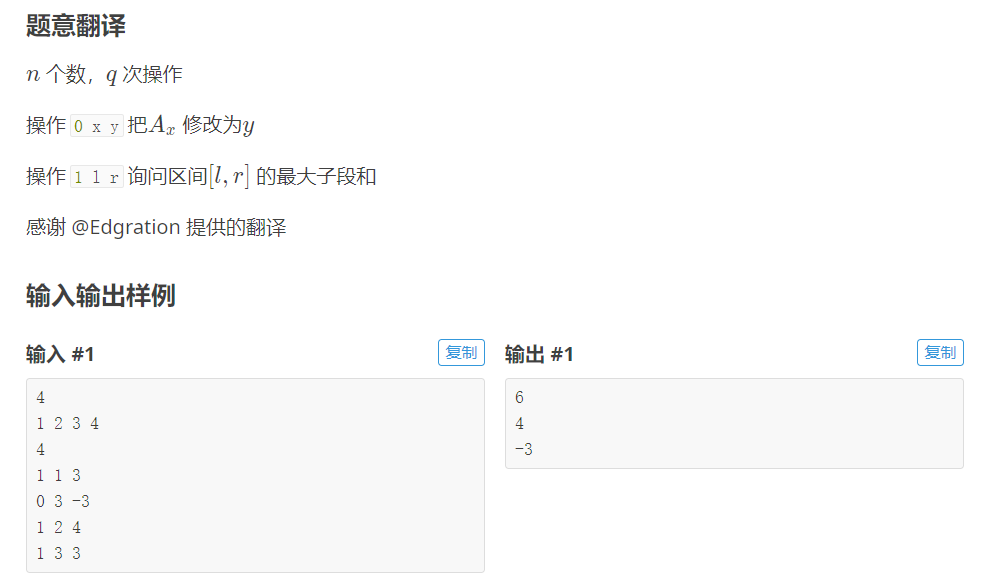
思路

//由于GSS3和GSS1几乎一毛一样，所以我就把GSS1的题解稍微改了一下就好了。

首先说明一下这道题的重难点。这道题由于只有一个单点赋值的操作，并要求我们求区间最大子段和，这个东西显然很不好维护（单点赋值很好做）。要维护它，我们先要看一下在查询和建树过程中

可能遇到的情况。
一、该区间的最大子段和完全被包括在它的左儿子中（如图）：

这样我们就可以把左儿子的最大子段和作为候选值加入。
——————————————————————————————————————
二、该区间的最大子段和完全被包括在它的右儿子中（如图）：

这样我们就可以把右儿子的最大子段和作为候选值加入。
——————————————————————————————————————
三、该区间的最大子段和在左儿子和右儿子都有一部分（如图）：

这种情况比上两种稍稍复杂一点，仔细想一下，我们就可以发现，这种情况下的最大子段和即为左儿子的最大后缀和加上右儿子的最大前缀和。为什么这样是正确的呢？因为我们要求最大子段和，

最大子段和的定义就是在一个序列中的所有子串中的和最大的那个（我有点说不清楚QWQ，但应该很好理解）。说白了，我们要让一个点所在的区间长度最大，就要让这个点两边的区间长度都最大

（有点类似于贪心的感觉）。把这个值作为候选值加入。

这样的话，我们就有了维护区间最大子段和的基本方法。我们对上述三种情况岁统计出来的值全都取一个max，然后就可以得出这个区间的最大子段和。

解决了上述去最大子段和的问题，我们又引申出来了两个新问题，那就是怎样维护区间最大前缀和和区间最大后缀和。由于这两个东西的维护方法非常类似（同时也是因为我懒），我就只给出区间

最大前缀和的维护方法。

同样是分情况讨论：
一、区间最大前缀和被完全包括在该区间的左儿子中（如图）：

这样我们就可以把左儿子的最大前缀和作为候选值加入。

二、区间最大前缀和在该区间的左儿子和右儿子都有一部分（如图）：

这样我们就可以看出，此时的最大前缀和就可以表示为左儿子的区间和加右儿子的最大前缀和，并把这个值作为候选值加入。

最后只要对上述两个值取个max就行……

区间最大后缀和和区间最大前缀和的维护方法几乎一毛一样，就是把区间最大前缀和翻转了一下而已，所以我觉得没有必要写了，毕竟也没啥不好理解的。

再就是在查询的时候对上面说的求最大子段和的方法中提到的三个值分别分类讨论一下（千万不要照着线段树模板的query写啊）。

关于update操作，对于本题来说基本没什么难度（更何况还是区间赋值），具体就看代码好了。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define MAXN 50010
typedef long long ll;
int n, m, a[MAXN];
struct node{
    ll val_f, val_b;//val_f维护区间最大前缀和，val_b维护区间最大后缀和
    ll val_sum;//区间和
    ll val_mal;//区间最大子段和
} tree[MAXN << 2];
inline int lson(int k) { return k << 1; }
inline int rson(int k) { return k << 1 | 1; }
inline void push_up(int k){
    tree[k].val_sum = tree[lson(k)].val_sum + tree[rson(k)].val_sum;//更新区间和
    tree[k].val_f = std::max(tree[lson(k)].val_sum + tree[rson(k)].val_f, tree[lson(k)].val_f);//更新区间最大前缀和
    tree[k].val_b = std::max(tree[rson(k)].val_sum + tree[lson(k)].val_b, tree[rson(k)].val_b);//更新区间最大后缀和
    tree[k].val_mal = std::max(tree[lson(k)].val_b + tree[rson(k)].val_f, std::max(tree[lson(k)].val_mal, tree[rson(k)].val_mal));
    return;//更新区间最大子串和，上述式子不明白的去看上面的推导
}
void build(int k,int l,int r){
    if(l==r){
        tree[k].val_sum = a[l];
        tree[k].val_f = tree[k].val_b = a[l];
        tree[k].val_mal = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(lson(k), l, mid);
    build(rson(k), mid + 1, r);
    push_up(k);
}
void update(int k,int l,int r,int x,ll v){
    if(l==r&&l==x){//update操作十分鸡肋，只要在遍历到需要修改的节点后修改，然后pushup即可
        tree[k].val_sum = v;
        tree[k].val_f = tree[k].val_b = v;
        tree[k].val_mal = v;
        return;
    }
    int mid = (l + r) >> 1;
    if(x<=mid)
        update(lson(k), l, mid, x, v);
    if(x>mid)
        update(rson(k), mid + 1, r, x, v);
    push_up(k);
}
node query(int k,int ql,int qr,int l,int r){//这里query的返回值定义为node，是为了更方便地查询和分类讨论
    if(ql<=l&&r<=qr)//这也就是为什么这道题写结构体线段树会好一点
        return tree[k];
    int mid = (l + r) >> 1;
    if(qr<=mid)//分类讨论1：区间全部在左子树
        return query(lson(k), ql, qr, l, mid);
    if(ql>mid)//分类讨论2：区间全部在右子树
        return query(rson(k), ql, qr, mid + 1, r);
    node ls, rs, res;//分类讨论3：区间在左右子树都有
    ls = query(lson(k), ql, qr, l, mid);
    rs = query(rson(k), ql, qr, mid + 1, r);
    res.val_sum = ls.val_sum + rs.val_sum;
    res.val_f = std::max(ls.val_f, ls.val_sum + rs.val_f);
    res.val_b = std::max(rs.val_b, rs.val_sum + ls.val_b);
    res.val_mal = std::max(ls.val_b + rs.val_f, std::max(ls.val_mal, rs.val_mal));
    return res;//上述分类讨论3的查询过程和pushup完全相同
}
int main(){
    scanf("%d", &n);
    for (int i = 1; i <= n;++i)
        scanf("%d", &a[i]);
    build(1, 1, n);
    scanf("%d", &m);
    for (int i = 1; i <= m;++i){
        int opt = 0;
        int x = 0, y = 0;
        scanf("%d", &opt);
        scanf("%d%d", &x, &y);
        if(opt==0)
            update(1, 1, n, x, y);
        if(opt==1)
            printf("%lld\n", query(1, x, y, 1, n).val_mal);
    }
    return 0;
}