Luogu P6190 [NOI Online #1 入门组]魔法

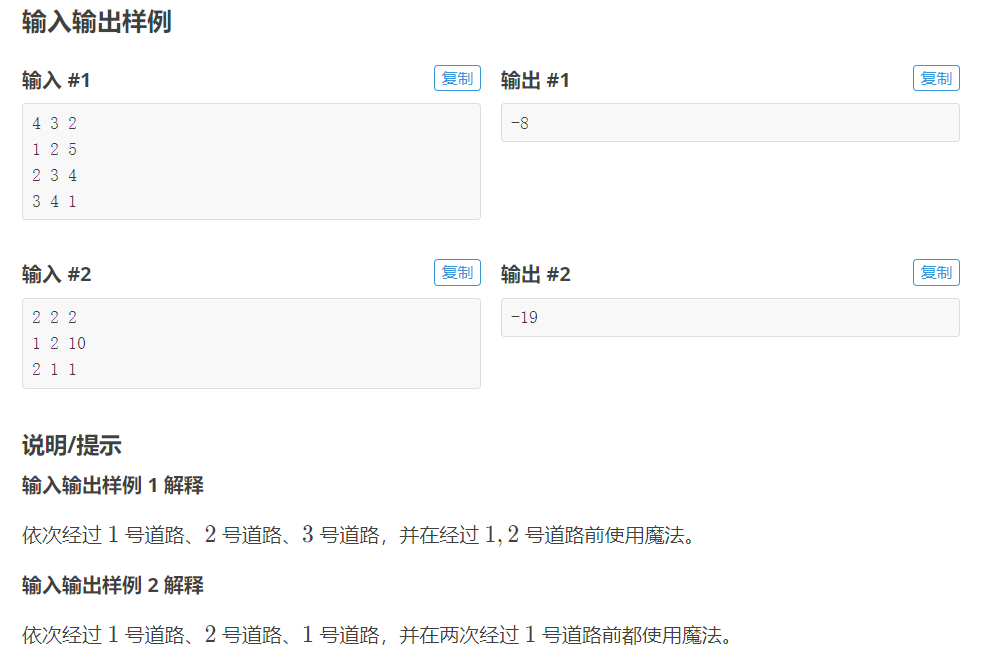
思路
一、30pts做法
这种做法简直简单到爆炸,\(k==0\)的情况只要跑最短路即可。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define INF 0x7fffffff
#define MAXN 2510
typedef long long ll;
int n, m, p;
ll f[MAXN][MAXN];
int main(){
scanf("%d%d", &n, &m);
scanf("%d", &p);
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
i == j ? f[i][j] = 0 : f[i][j] = INF;
}
for (int i = 1; i <= m; ++i){
int u, v, w;
scanf("%d%d", &u, &v);
scanf("%d", &w);
f[u][v] = w;
}
for (int k = 1; k <= n;++k){
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
f[i][j] = std::min(f[i][j], f[i][k] + f[k][j]);
}
}
printf("%lld\n", f[1][n]);
return 0;
}
70pts做法
关于70pts做法,其实已经和正解十分的接近,就差在了优化上(所以可见对于某些DP和搜索优化有多么重要)。
现在我们可以通过30pts的做法(直接跑最短路)知道当\(k==0\)的时候的结果。这样我们可以考虑如何从\(k==0\)的情况转移到\(k==1\)的情况。
我们设\(g[i][j][k]\)表示从第\(i\)个点到第\(j\)个点使用不超过\(k\)次魔法的情况下的最短路。那现在我们通过floyd可以求出\(g[i][j][0]\),那么怎么得到\(g[i][j][1]\)呢?
这里可以考虑遍历每一条边。由于此题\(m \leq 2500\),所以枚举并不会让你炸掉。转移时我们枚举要用魔法的边,然后在转移的时候强制走这条边,求出最短路。如果假设边\((u,v,w)\)使用了魔法,
那么这种情况先很显然转移方程就是\(g[i][j][1]=min(g[i][u][0]+g[v][j][0]-w,min(g[i][j][0],g[i][j][1]))\) 。
这样我们就得到了\(k==1\)的情况。现在不要着急一步得出结论,我们先来看一下从\(k==1\)如何转移到\(k==2\) 。
这个做法就类似于floyd。我们枚举一条从\(i\)到\(j\)的边的中转点\(k\),然后在\(i\)$k$这个区间用一次魔法,在$k$\(j\)这个区间在用一次魔法(用一次魔法的转移方法与从\(k==0\)转移到\(k==1\)的方
法类似),然后将两个区间的答案和并即为\(k==2\)时的答案。这样的话转移方程即为\(g[i][j][2]=min(g[i][j][2],g[i][k][1]+g[k][j][1])\) 。
而根据\(k==2\)的情况,我们可以发现如果我们把最多使用\(i\)次魔法的答案和最多使用j次魔法的情况进行合并,就可以得到最多使用\(i+j\)次魔法的答案。这样对于70pts做法,我们就可以得到对于其
他情况的处理方法。我们先枚举使用魔法的次数\(s\),再枚举从点\(i\)到点\(j\)的中转点\(k\),假设在\(i\)$k$这个区间使用了$s$-$1$次魔法,在$k$\(j\)这个区间使用了\(1\)次魔法,按照这个方法进
行转移。至于为什么要这么做,我们实现时其实是先处理出\(k==1\)的情况,在再枚举\(k>1\)的情况,这样的话我们才有方法转移(如果不这样做那你还能怎么转移)。这样的话我们就可以得出最多使用\(s\)
次魔法时的转移方程为\(g[i][j][s]=min(,g[i][j][s],g[i][k][s-1]+g[k][j][1])\) 。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define INF 0x3f
#define MAXN 110
using std::cout;
typedef long long ll;
int n, m, p;
ll f[MAXN][MAXN], g[MAXN][MAXN][MAXN];
struct node{
int u, v, w;
} edge[2550];//由于之后的枚举中要用到边的信息,所以我们要把边的信息存储下来
int main(){
scanf("%d%d", &n, &m);
scanf("%d", &p);
std::memset(f, 0x3f, sizeof(f));
std::memset(g, 0x3f, sizeof(g));
for(int i=1;i<=n;++i)f[i][i]=0;//这里注意每个点到自己的距离为0
for (int i = 1; i <= m; ++i){
scanf("%d%d", &edge[i].u, &edge[i].v);
scanf("%d", &edge[i].w);
f[edge[i].u][edge[i].v] = edge[i].w;//把边的信息存到f数组中,方便DP使用
}
for (int k = 1; k <= n;++k){
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
f[i][j] = std::min(f[i][j], f[i][k] + f[k][j]), g[i][j][0] = f[i][j];
}//最普通的floyd,求当k==0时的情况
}
for (int k = 1; k <= m; ++k){
int u = edge[k].u, v = edge[k].v, w = edge[k].w;
for (int i = 1; i <= n; ++i){
for (int j = 1; j <= n; ++j)//这里要先处理出k==1是的情况,方便k>1的情况的转移
g[i][j][1] = std::min(g[i][u][0] + g[v][j][0] - w, std::min(g[i][j][0], g[i][j][1]));
}
}
for (int s = 1; s <= p;++s){
for (int k = 1; k <= n;++k){
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
g[i][j][s] = std::min(g[i][j][s], g[i][k][s - 1] + g[k][j][1]);
}
}
}
printf("%lld\n", g[1][n][p]);//输出
return 0;
}
100pts做法
虽然这个做法说是对70pts做法的优化,其实差别还是不小的。100pts做法需要的是将矩阵乘法的乘改为取min。而且,因为我们是要对不同的方案合并,所以还要证明这么做满足结合律。
现在进入正题……首先我们先要来说一下这道题的前置知识——矩阵快速幂。矩阵快速幂,顾名思义,就是用矩阵优化的快速幂(我感觉这说了跟没说一样)。
1.快速幂(注:因为时间关系,下列内容除代码外都来自网络,望大家谅解)
快速幂其实说白了就会让你的乘方算法变得更快(而且不是快一星半点)。
该怎样去加速幂运算的过程呢?既然我们觉得将幂运算分为\(n\)步进行太慢,那我们就要想办法减少步骤,把其中的某一部分合成一步来进行。
比如,如果\(n\)能被\(2\)整除,那我们可以先计算一半,得到\(a^{n/2}\)的值,再把这个值平方得出结果。这样做虽然有优化,但优化的程度很小,仍是线性的复杂度。
再比如,如果我们能找到\(2^k=n\),我们就能把原来的运算优化成:\(((a^2)^2)^2...\),只需要\(k\)次运算就可以完成,效率大大提升。可惜的是,这种条件显然太苛刻了,适用范围很小。不过这给了我们一
种思路,虽然我们很难找到\(2^k=n\),但我们能够找到\(2^{k_1}+2^{k_2}+2^{k_3}+......+2^{k_m}=n\)。这样,我们可以通过递推,在很短的时间内求出各个项的值。
我们都学习过进制与进制的转换,知道一个\(b\)进制数的值可以表示为各个数位的值与权值之积的总和。比如,2进制数\(10011001\),它的值可以表示为10进制的\(1\times 2^3+0\times 2^2+0\times 2^1+1\times 2^0\),即9。
这完美地符合了上面的要求。可以通过2进制来把\(n\)转化成\(2^{k_m}\)的序列之和,而2进制中第\(i\)位(从右边开始计数,值为1或是0)则标记了对应的\(2^{i−1}\)是否存在于序列之中。
譬如,13为二进制的\(11011101\),他可以表示为\(2^3+2^2+2^0\),其中由于第二位为0,\(2^1\)项被舍去。
如此一来,我们只需要计算\(a\)、\(a^2\)、\(a^4\)、\(a^8\)......的值(这个序列中的项不一定都存在,由\(n\)的二进制决定)并把它们乘起来即可完成整个幂运算。借助位运算的操作,可以很方便地
实现这一算法,其复杂度为\(O(log_2 n)\) 。

2.矩阵快速幂
(1)矩阵乘法
简单的说矩阵就是二维数组,数存在里面,矩阵乘法的规则:A*B=C
一个nm的矩阵可以和一个ma的矩阵相乘得到一个n*a的矩阵。
对于结果C,满足:
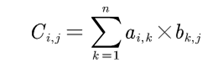
不理解?我们可以举个栗子:
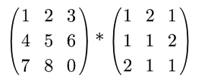
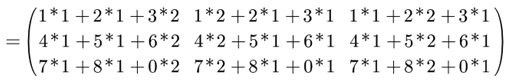
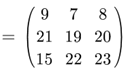
矩阵乘法也就这么多,没有太多可以赘述的。
(2)矩阵快速幂
矩阵快速幂,说白了就是把快速幂里的乘法换成矩阵乘法就行了。由矩阵乘法的定义可知,如果a*a合法,那么a的行等于a的列,所以快速幂的矩阵必须是方阵(行和列相等)。要找到一个方阵a,
使与a边长相同的矩阵乘a结果等于它本身。这里的a只有对角线是1,其他的值都为0,这时能保证与a边长相同的矩阵乘a结果等于它本身。
对于矩阵快速幂的代码,由于时间原因,我没法都写出来,这部分的代码在下面的满分代码中会有涉及。
那么,说了这么多,此题应该如何使用矩阵快速幂来优化呢?
对于一个邻接矩阵P,那么\(P^k\)表示的就是恰好经过k步后的状态。摘自题解。
假设我们有一个矩阵P,P(i,j)表示的就是在1步内从i到j的方案数。很显然,这个矩阵内只会有0,1两种数。对这个矩阵做k遍矩阵乘法之后,得到的矩阵P’就是恰好走了k步时从i到j的方案数。
举个例子:
假设原矩阵为:
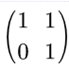
我们对他进行3次矩阵乘法
第一次得到:
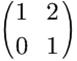
第二次得到:
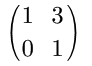
第三次得到:
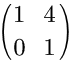
这样应该就会很形象生动了……在不懂的话可以自己手推一下。
这么做的话其实就可以用矩阵快速幂来完成一部分的动态规划,以达到节省时间的目的。只是为了满足题目的要求,这里的矩阵乘法的定义需要改变,即把乘法改为取min的操作。至于为什么这样做可
以,我也不太清楚(我太菜了)。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define MAXN 110
#define INF 1e15+100
typedef long long ll;
int n, m, p;
ll f[MAXN][MAXN];
struct node{
int u, v, w;
} edge[2550];
struct Matrix{
ll a[MAXN][MAXN];
} g;//这里把矩阵存放在结构体里,方便快速幂之后返回结果
Matrix operator*(const Matrix &a,const Matrix &b){//重载运算符
Matrix res;
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
res.a[i][j] = INF;
}//初始化res数组,全部赋值为INF,因为下面取最小值
for (int k = 1; k <= n;++k){
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
res.a[i][j] = std::min(res.a[i][j], a.a[i][k] + b.a[k][j]);
}//这里的做法和floyd的写法极其类似,这里也就是相当于完成矩阵乘法
}
return res;
}
Matrix Quick_pow(Matrix a,int k){//矩阵快速幂
Matrix res;
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
res.a[i][j] = f[i][j];
}//先把f数组的值存储到res里,方便操作
while(k){
if(k&1)//若二进制k最后一位为1
res = res * a;//做矩阵乘法
a = a * a;//对a平方
k >>= 1;//把二进制k的最后一位舍掉
}
return res;
}
int main(){
scanf("%d%d",&n,&m);
scanf("%d", &p);
memset(f, 0x3f, sizeof(f));
memset(g.a, 0x3f, sizeof(g.a));
for (int i = 1; i <= n;++i)
f[i][i] = 0;//初始化
for (int i = 1; i <= m; ++i){
scanf("%d%d", &edge[i].u, &edge[i].v);
scanf("%d", &edge[i].w);
f[edge[i].u][edge[i].v] = edge[i].w;
}//读入
for (int k = 1; k <= n;++k){
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
f[i][j] = std::min(f[i][j], f[i][k] + f[k][j]);
}
}//floyd部分
if(p==0){
printf("%lld\n", f[1][n]);
return 0;
}//这里需要特判,因为任何数的0次幂都等于1,如果直接做矩阵乘法会炸
for (int k = 1; k <= m;++k){
int u = edge[k].u, v = edge[k].v, w = edge[k].w;
for (int i = 1; i <= n;++i){
for (int j = 1; j <= n;++j)
g.a[i][j] = std::min(f[i][u] + f[v][j] - w, std::min(g.a[i][j], f[i][j]));
}//这里处理出k==1时的结果,完善矩阵快速幂所需要的矩阵
}
printf("%lld\n", Quick_pow(g, p).a[1][n]);//输出
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号