Luogu P4314 CPU监控

思路

对于这道题，为了好想，我们先考虑一下如果不考虑历史最大值应该怎么做。这样的话，我们需要做区间加和区间推平的操作。那么，做过线段树2的都知道，我们应该是需要两个tag来维护，分别是区

间累加和区间推平。那么对于这个题，我们怎么在pushdown的时候兼容这两个tag呢？

很显然，无论你先做区间加还是先做区间推平都是不行的。假设我们有这样一个操作序列：+1 +2 +4 推平2 +5 -3 。很显然按照给出的操作序列，得到的结果是4。如果我们先做区间加，再做区间推

平，那么得到的结果是2，这很明显不对。那如果我们先做区间推平，再做区间加，那么得到的结果是11，这很明显也不对……那我们应该怎么做呢？
很明显，影响整个过程的是区间推平操作。区间推平之前的区间加操作其实是不受影响的，问题就是在区间推平之后的区间加操作。在C++语法中，我们知道b += c和b = b + c是等价的。根据这个，

我们可以考虑把在第一次区间推平之后的所有区间加操作转化为区间推平操作。这个具体实现一会在代码里写。
那如果加上维护历史最大值的操作，应该怎么做呢？和维护当前区间最大值类似，我们也是要维护区间累加和区间推平，然后在更新的时候注意要用未更新前的当前最大值更新，不要扰乱时间线。但是，

单单和当前区间最大值一样维护是不行的。比如下面这种情况：

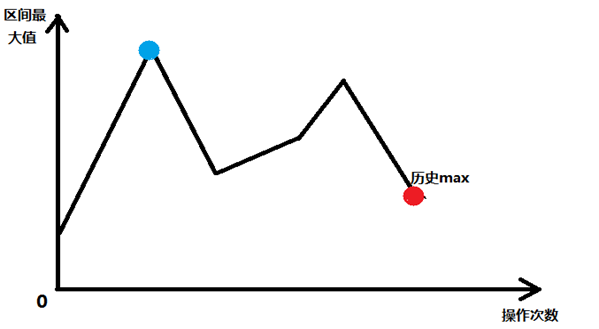
对于这样的一个操作序列，如果我们仅仅是把历史最大值和当前最大值一起做更新（即只考虑把tag全部放下之后的情况）就会导致上面这种情况。很明显，这张图的历史最大值是在蓝色点所在处。

因为tag中是集成了所有询问和更新之前的操作，所以历史最大值很可能是出现在中间过程，而不是最后结果。那该怎么办呢？

有人可能会直接想到每次更新之后直接下放标记。但这样做会让你线段树优秀的\(O(n log n)\) 时间复杂度暴涨至\(O(n^2logn)\) 。然后你就过不了这道题了。

那该如何做呢？我们需要把维护历史最大的两个标记的定义更改一下。我们让维护历史最大的两个标记分别定义为历史最大累加和历史最大推平，然后在更新维护当前的两个tag的时候一起更新，只不

过把加或者赋值改为取max了。维护的时候先下放已有的加法标记，再推平（这里因为第一次推平之后的所有加法都转化成了赋值，所以不会出现加法被覆盖的情况）。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define MAXN 100005
#define INF 0x7fffffff 
typedef long long ll;
int T, a[MAXN], E;
struct node{
    int nmax, hmax;//当前区间最大值、历史区间最大值
    int ntag1, htag1;//当前累加tag、历史最大累加tag
    int ntag2, htag2;//当前最大赋值tag、历史最大赋值tag
    int flag;//0表示没有被推平过，1表示已经被推平过
} tree[MAXN << 2];
inline int lson(int k) { return k << 1; }
inline int rson(int k) { return k << 1 | 1; }
inline void push_up(int k){
    tree[k].nmax = std::max(tree[lson(k)].nmax, tree[rson(k)].nmax);
    tree[k].hmax = std::max(tree[lson(k)].hmax, tree[rson(k)].hmax);
    return;//push_up没有什么特殊的，基本操作
}
void build(int k,int l,int r){
    tree[k].ntag1 = 0, tree[k].htag1 = 0;
    tree[k].ntag2 = -INF, tree[k].htag2 = -INF;
    tree[k].flag = 0;//这里初始化钦定-INF为没有推平
    if(l==r){
        tree[k].nmax = a[l], tree[k].hmax = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(lson(k), l, mid);
    build(rson(k), mid + 1, r);
    push_up(k);
}//建树操作
inline void change(int k,int nv,int hv){//赋值函数
    tree[k].flag = 1;//不要忘了把赋值标记设为1
    tree[k].htag2 = std::max(tree[k].htag2, hv);//这里是取max
    tree[k].ntag2 = nv;//维护赋值的两个tag
    tree[k].hmax = std::max(tree[k].hmax, hv);
    tree[k].nmax = nv;//更新赋值后的nmax和hmax
    return;
}
inline void add(int k,int nv,int hv){
    if(tree[k].flag == 1){
        change(k, tree[k].nmax + nv, tree[k].nmax + hv);
        return;//如果当前区间已经被推平过，那么把累加转化为推平
    }
    tree[k].htag1 = std::max(tree[k].htag1, tree[k].ntag1 + hv);
    tree[k].ntag1 += nv;//这里维护历史值的时候不要忘了是用当前值更新，否则会扰乱时间线
    tree[k].hmax = std::max(tree[k].hmax, tree[k].nmax + hv);
    tree[k].nmax += nv;//同上
    return;
}
inline void push_down(int k){
    add(lson(k), tree[k].ntag1, tree[k].htag1);
    add(rson(k), tree[k].ntag1, tree[k].htag1);//先下放已有的累加标记
    if(tree[k].flag == 1){
        change(lson(k), tree[k].ntag2, tree[k].htag2);
        change(rson(k), tree[k].ntag2, tree[k].htag2);
    }//若被推平过，下放推平标记，否则会漏掉一些操作（因为一些累加被转化为了推平）
    tree[k].flag = 0;//标记下放完了之后将标记复原
    tree[k].ntag1 = 0, tree[k].ntag2 = -INF;
    tree[k].htag1 = 0, tree[k].htag2 = -INF;
    return;
}
void update_add(int k,int l,int r,int cl,int cr,int v){
    if(cl<=l&&r<=cr){
        add(k, v, v);//这里给出的历史和当前是一样的，因为是更新操作
        return;
    }
    push_down(k);
    int mid = (l + r) >> 1;
    if(cl<=mid)
        update_add(lson(k), l, mid, cl, cr, v);
    if(cr>mid)
        update_add(rson(k), mid + 1, r, cl, cr, v);
    push_up(k);
}//update没什么可说的
void update_change(int k,int l,int r,int cl,int cr,int v){
    if(cl<=l&&r<=cr){
        change(k, v, v);
        return;
    }
    push_down(k);
    int mid = (l + r) >> 1;
    if(cl<=mid)
        update_change(lson(k), l, mid, cl, cr, v);
    if(cr>mid)
        update_change(rson(k), mid + 1, r, cl, cr, v);
    push_up(k);
}//同上
int query_now(int k,int l,int r,int ql,int qr){
    if(ql<=l&&r<=qr)
        return tree[k].nmax;
    push_down(k);
    int mid = (l + r) >> 1;
    int res = -INF;//取max不要忘了赋值为-INF
    if(ql<=mid)
        res = std::max(res, query_now(lson(k), l, mid, ql, qr));
    if(qr>mid)
        res = std::max(res, query_now(rson(k), mid + 1, r, ql, qr));
    return res;
}
int query_history(int k,int l,int r,int ql,int qr){
    if(ql<=l&&r<=qr)
        return tree[k].hmax;
    push_down(k);
    int mid = (l + r) >> 1;
    int res = -INF;
    if(ql<=mid)
        res = std::max(res, query_history(lson(k), l, mid, ql, qr));
    if(qr>mid)
        res = std::max(res, query_history(rson(k), mid + 1, r, ql, qr));
    return res;
}//同上
int main(){
    scanf("%d",&T);
    for (int i = 1; i <= T;++i)
        scanf("%d", &a[i]);
    build(1, 1, T);//千万不要忘了建树啊
    scanf("%d", &E);
    for (int i = 1; i <= E;++i){
        char opt[20];
        int x = 0, y = 0, z = 0;
        scanf("%s", opt);
        scanf("%d%d", &x, &y);
        if(opt[0]=='Q')
            printf("%d\n", query_now(1, 1, T, x, y));
        if(opt[0]=='A')
            printf("%d\n", query_history(1, 1, T, x, y));
        if(opt[0]=='P'){
            scanf("%d", &z);
            update_add(1, 1, T, x, y, z);
        }
        if(opt[0]=='C'){
            scanf("%d", &z);
            update_change(1, 1, T, x, y, z);
        }
    }//主函数没有什么特别的
    return 0;