Luogu P1531 I Hate It

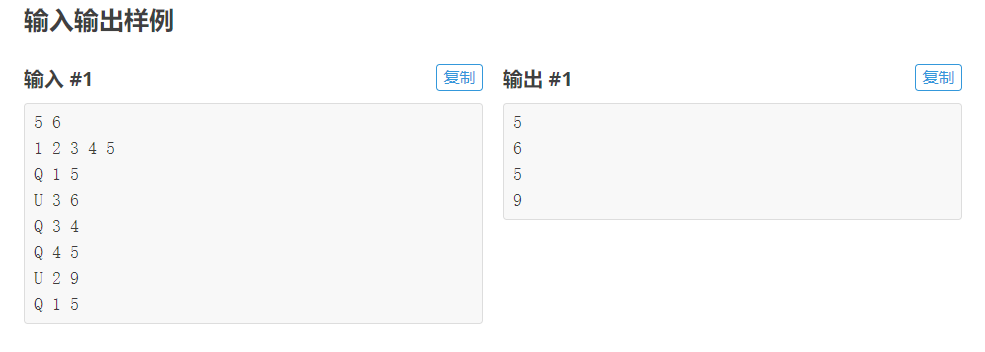
思路

这道题其实并不难，充其量就是一道线段树（单点修改+区间维护最大值）的板子。但是基于严谨务实的态度，我们还是应该认真看一下这个道题。

线段树的基本写法及原理在这里不再赘述，下面我们来说一下单点修改操作。

这道题的单点修改操作跟线段树板子的单点修改不太一样，这道题的单点修改不是单纯地将一个点的值改为另一个值，而是对当前点的原本的值与给定的值取一个最大值（其实也没啥区别，就是在update

的时候把替换操作改为对两个值取max即可）。单点修改就这些，其实就是把线段树板子稍稍改动了一下。

区间查询操作也很简单，说白了就是把区间求和的操作改成区间求最大值即可。具体操作就是把push_up、build、update和query操作中的求和改为取max即可。具体细节还是看代码吧。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define INF 0x7fffffff
#define MAXN 2000010
typedef long long ll;
//以上应该没有疑问
ll n, m, a[MAXN];
ll tree[MAXN<<2];
inline ll read(void){//快读，其实我也没用到
    ll x = 0, f = 1;char ch;
    do{ch = getchar();if (ch == '-' )f = -1;}while(ch < '0' || ch > '9');
    do{x = x * 10 + ch - '0';ch = getchar();}while (ch >= '0' && ch <= '9');
    return f * x;
}
//求左儿子
inline ll lson(ll k) { return k << 1; }
//求右儿子
inline ll rson(ll k) { return k << 1 | 1; }
//上传操作，注意是求max，不是求和
inline void push_up(ll k){
    tree[k] = std::max(tree[lson(k)], tree[rson(k)]);
    return;
}
//建树（主程序里一定不要忘了执行啊！）
void build(ll l,ll r,ll k){
    if(l==r){//若遍历到叶子结点，直接赋值
        tree[k] = a[l];
        return;
    }
    //否则分别遍历左右子树
    ll mid = (l + r) >> 1;
    //遍历左子树
    build(l, mid, lson(k));
    //遍历右子树
    build(mid+1,r,rson(k));
    //别忘了上传
    push_up(k);
    return;
}
void update(ll x,ll l,ll r,ll k,ll v){
    if(l==r&&l==x){//若当前节点为需要更改的点
        tree[k] = std::max(tree[k], v);//更改取max
        return;
    }
    ll mid = (l + r) >> 1;
    //若有一部分在左子树，向左子树遍历
    if(x<=mid)update(x,l,mid,lson(k),v);
    //若有一部分在右子树，向右子树遍历
    else update(x,mid+1,r,rson(k),v);
    //上传
    push_up(k);
}
ll query(int ql,int qr,int l,int r,int k){
    ll res = -INF;//赋值成-INF比较保险
    if(ql<=l&&r<=qr)return tree[k];//若当前区间被查询区间完全包括，直接返回
    ll mid = (l + r) >> 1;
    //若查询区间一部分在左子树，遍历左子树
    if(ql<=mid)res=std::max(res,query(ql,qr,l,mid,lson(k)));
    //若查询区间一部分在右子树，遍历右子树
    if(qr>mid)res=std::max(res,query(ql,qr,mid+1,r,rson(k)));
    return res;
}
int main(){
    scanf("%lld%lld",&n,&m);
    for (int i = 1; i <= n;++i)
        scanf("%lld",&a[i]);
    //读入……
    build(1,n,1);//千万别忘了建树
    for (int i = 1; i <= m;++i){
        char opt[20];
        scanf("%s", opt);//读入……
        if(opt[0]=='Q'){
            ll x = 0, y = 0;//查询x~y区间内的最大值
            scanf("%lld%lld", &x, &y);
            printf("%lld\n", query(x, y, 1, n, 1));
        }
        if(opt[0]=='U'){
            ll x = 0, y = 0;
            scanf("%lld%lld", &x, &y);
            //将x位置的数与y取max
            update(x, 1, n, 1, y);
        }
    }
    return 0;
}