Luogu P1471 方差

思路

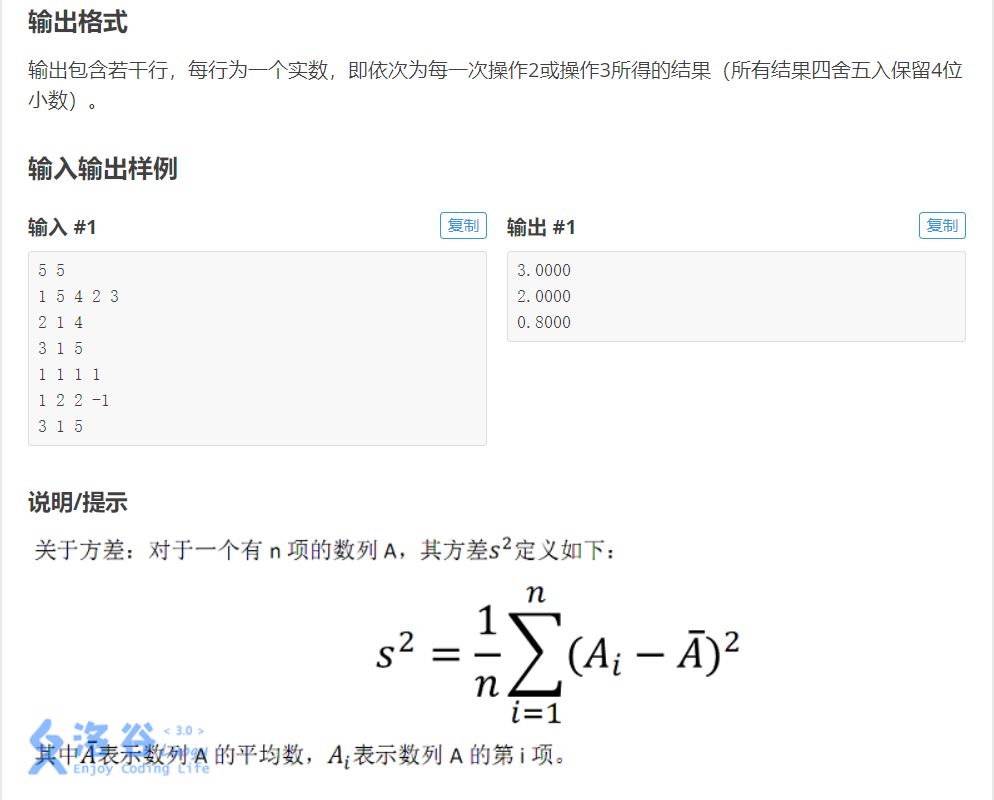
现在进入正题。这道题要求我们维护区间平均数和区间方差。很显然，区间平均数是很好维护的，我们只要维护一下区间和，在求平均数的时候用区间和除以区间长度即可。那么我们怎么来维护方差呢？很

明显直接维护是不现实的，所以我们要对方差的公式进行推导：

利用我们最后推出的这个公式，我们可以看出我们只要在多维护一个平方和，就可以轻松地求出方差。维护区间平方和的方法和维护区间和的方法没什么区别，只是把每一项的值改成了平方再相加。如果还

是不懂的话等下看代码吧。

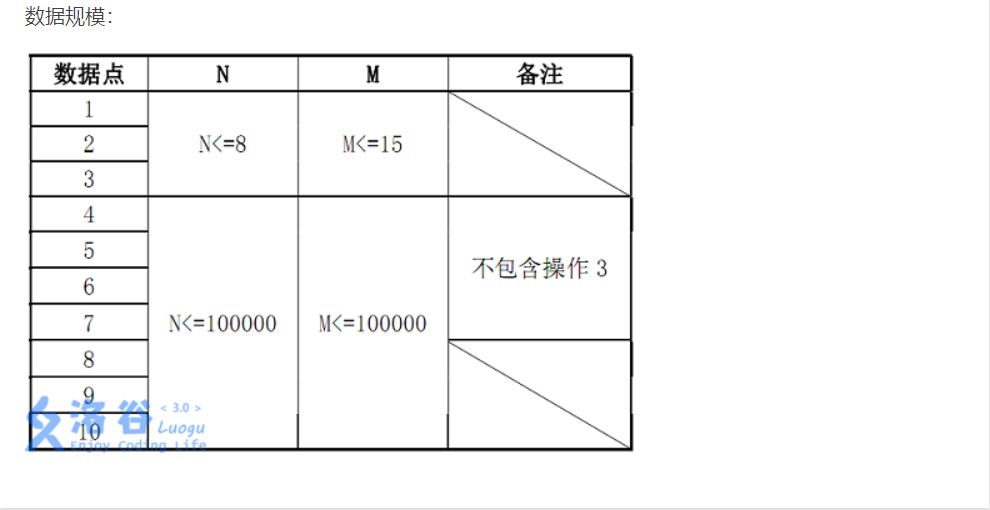
最后还有一个问题就是如何高效地更新区间平方和。一样，我们还是要推式子：

这样的话我们就可以利用原本的平方和和原本的区间和来完成对区间平方和的更新操作。更多的细节看代码吧。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<string>
#define MAXN 100010
typedef long long ll;
int n, m;
double a[MAXN];
struct node{
    double val_sum,val_squ;//sum维护的是区间和，squ维护区间平方和
    double tag;//懒标记
} tree[MAXN << 2];
inline int lson(int k) { return k << 1; }
inline int rson(int k) { return k << 1 | 1; }
inline void push_up(int k){
    tree[k].val_sum = tree[lson(k)].val_sum + tree[rson(k)].val_sum;
    tree[k].val_squ = tree[lson(k)].val_squ + tree[rson(k)].val_squ;
    return;//上传都是照常上传，没有什么特殊的
}
inline void push_down(int k,int l,int r){
    int mid = (l + r) >> 1;
    tree[lson(k)].tag += tree[k].tag;
    tree[rson(k)].tag += tree[k].tag;
    tree[lson(k)].val_squ += 2.0 * tree[k].tag * tree[lson(k)].val_sum + (mid - l + 1) * tree[k].tag * tree[k].tag;
    tree[rson(k)].val_squ += 2.0 * tree[k].tag * tree[rson(k)].val_sum + (r - mid) * tree[k].tag * tree[k].tag;
    tree[lson(k)].val_sum += tree[k].tag * (mid - l + 1);
    tree[rson(k)].val_sum += tree[k].tag * (r - mid);
    tree[k].tag = 0;//这里的维护区间平方和的操作利用的就是推的公式，不明白的自己套公式就可以了
    return;
}
void build(int k,int l,int r){
    tree[k].tag = 0;
    if(l==r){
        tree[k].val_sum = a[l];
        tree[k].val_squ = a[l] * a[l];//不要忘了平方
        return;
    }
    int mid = (l + r) >> 1;
    build(lson(k), l, mid);
    build(rson(k), mid + 1, r);
    push_up(k);//不再解释
}
void update(int k,int cl,int cr,int l,int r,double v){
    if(cl<=l&&r<=cr){//这里的更新也同样利用的公式，不懂的去上面找公式自己套
        tree[k].val_squ += 2.0 * v * tree[k].val_sum + (r - l + 1) * v * v;
        tree[k].val_sum += (r - l + 1) * v;
        tree[k].tag += v;
        //这里的更新顺序一定要注意！一定是先更新区间平方和再更新区间和
        //因为我们更新区间平方和的时候利用的是更新之前的区间和
        //据说顺序写错还能得40……
        return;
    }
    push_down(k, l, r);
    int mid = (l + r) >> 1;
    if(cl<=mid)
        update(lson(k), cl, cr, l, mid, v);
    if(cr>mid)
        update(rson(k), cl, cr, mid + 1, r, v);
    push_up(k);//也不再解释
}
double query_sum(int k,int ql,int qr,int l,int r){//求区间和
    double res = 0;
    if(ql<=l&&r<=qr)
        return tree[k].val_sum;
    push_down(k, l, r);
    int mid = (l + r) >> 1;
    if(ql<=mid)
        res += query_sum(lson(k), ql, qr, l, mid);
    if(qr>mid)
        res += query_sum(rson(k), ql, qr, mid + 1, r);
    return res;//也不再解释
}
double query_squ(int k,int ql,int qr,int l,int r){//求区间平方和
    double res = 0;
    if(ql<=l&&r<=qr)
        return tree[k].val_squ;
    push_down(k, l, r);
    int mid = (l + r) >> 1;
    if(ql<=mid)
        res += query_squ(lson(k), ql, qr, l, mid);
    if(qr>mid)
        res += query_squ(rson(k), ql, qr, mid + 1, r);
    return res;//也不再解释
}
int main(){
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n;++i)
        scanf("%lf", &a[i]);
    build(1, 1, n);
    for (int i = 1; i <= m;++i){
        int opt = 0;
        int x = 0, y = 0;
        scanf("%d", &opt);
        scanf("%d%d", &x, &y);
        if(opt==1){
            double k = 0;
            scanf("%lf", &k);
            update(1, x, y, 1, n, k);
        }
        if(opt==2){
            double ret = query_sum(1, x, y, 1, n);
            printf("%.4lf\n", ret / (y - x + 1));//求平均数
        }
        if(opt==3){
            double ret0 = query_sum(1, x, y, 1, n) / (y - x + 1) * 1.0;
            double ret1 = query_squ(1, x, y, 1, n) / (y - x + 1) * 1.0;
            printf("%.4lf\n", ret1 - ret0 * ret0);//这里利用的也是上面的公式
            //不明白的可以自己去套一下
        }
    }
    return 0;
}