Luogu P1197 [JSOI2008]星球大战

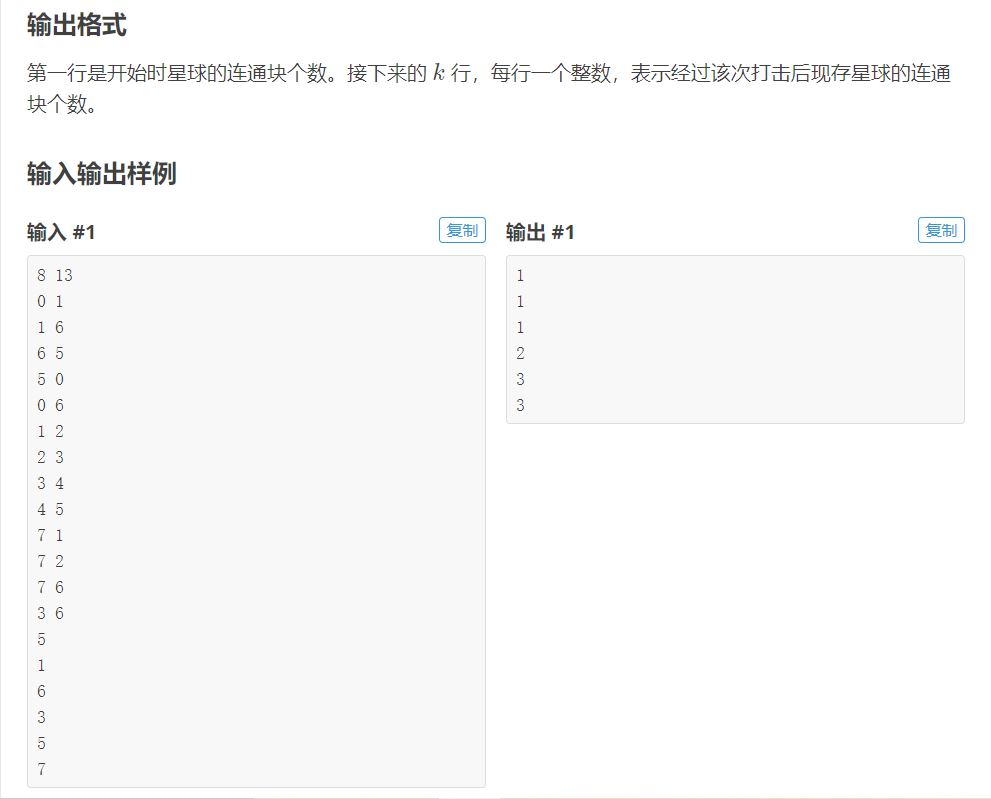
思路

这个题表面看好像是一个并查集删点操作，但是并查集貌似并没有类似的操作，只有加点和查询操作。那怎么办呢？这时候逆向思维就显得尤为重要。

我们可以考虑删点操作转化为加点操作。把题目中给出的删点序列逆转，第一次建成的并查集是执行完所有删点操作的并查集，然后按照题目中给出顺序的逆序执行加点操作，每次统计形成的连通块个数

（即父亲为自己的的点的个数，但是为了让时间更优秀，我们实际并不是这么统计的）。

最后把逆序统计出的答案存到数组里，最后逆序输出即可。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define MAXN 400005
int n, m, k, f[MAXN];
int p[MAXN], h[MAXN];//p是要删的点的编号，h是标记哪个点要删
int head[MAXN], cnt;//链式前向星存图
int res[MAXN];//答案
inline int read(void){
    int f = 1, x = 0;char ch;
    do{ch = getchar();if(ch=='-')f = -1;} while (ch < '0' || ch > '9');
    do{ x = x * 10 + ch - '0';ch = getchar();} while (ch >= '0' && ch <= '9');
    return f * x;
}
struct node{
    int from, nxt, to;
} edge[MAXN];//这里要多加一个from，统计上一个点是谁，下面要用到
inline void add_edge(int x,int y){
    ++cnt;
    edge[cnt].nxt = head[x];
    edge[cnt].from = x;
    edge[cnt].to = y;
    head[x] = cnt;
    return;
}//链式前向星存图
inline int get_father(int k){
    return f[k] == k ? k : f[k] = get_father(f[k]);
}//寻根
inline void merge(int x,int y){
    f[get_father(x)] = get_father(y);
    return;
}//合并
int main(){
    n = read(), m = read();
    for (int i = 0; i <= n;++i)
        f[i] = i;//初始化
    for (int i = 1; i <= m;++i){
        int u = read(), v = read();
        add_edge(u, v), add_edge(v, u);//连双向边
    }
    k = read();
    for (int i = 1; i <= k;++i)
        p[i] = read(), h[p[i]] = 1;//把要删的点标记为 1
    int tot = n - k;//删完点后点的数量
    for (int i = 1; i <= cnt; ++i){
        if(h[edge[i].from]==0 && h[edge[i].to]==0 && get_father(edge[i].from)!=get_father(edge[i].to)){
            --tot, merge(edge[i].from, edge[i].to);//如果该边上的两个点都没有被删过，且不在同一个并查集里，合并，联通块数量减一
        }
    }
    res[k + 1] = tot;//存下删完所有点之后的联通块数量
    for (int i = k; i >= 1;--i){
        ++tot, h[p[i]] = 0;//加上一个点
        for (int j = head[p[i]]; j;j=edge[j].nxt){//遍历所有与它相连的边
            if(h[edge[j].to]==0 && f[get_father(p[i])]!=f[get_father(edge[j].to)]){
                --tot, merge(edge[j].to, p[i]);//若该边连到的点当前没有被删除，且这两个点不在同一联通块中，合并，联通块数量减一
            }
        }
        res[i] = tot;//统计答案
    }
    for (int i = 1; i <= k+1;++i)
        printf("%d\n", res[i]);//最后输出不要忘了还有初始状态
    return 0;
}