佩尔方程的运用

题目:

Do u like arithmetic sequence~
Satisfy:
  ->n1 > 2**0x149f and n2 > 2**0x149f
  ->AS(1, n1, n1) = 0x149f * AS(1, 1 + 2 * (n2 - 1), n2)
******************************************************
 [1]Sample~ 
 [2]I want get the flag!!! 
 [3]QUIT. 
******************************************************

解题思路:

分析代码

等差数列数学题

• 左侧序列:AS(1, n1, n1)
  • 首项:a=1
  • 末项:L=n1
  • 项数:n=n1
  • 公差:d=L−a/n−1=n1−1/n1−1=1
  • 和公式:S<sub>左</sub>=(n/2)⋅(a+L)=(n1/2)⋅(1+n1)
• 右侧序列:AS(1, 1 + 2⋅(n2 -1), n2)
  • 首项:a=1
  • 末项:L=1+2(n2−1)=2n2−1
  • 项数:n=n2
  • 公差:d=L−a/n−1=2n2−2/n2−1=2
  • 和公式:S<sub>右</sub>=(n/2)⋅(a+L)=(n2/2)⋅(1+2n2−1)=(n2/2)⋅2n2=n2<sup>2</sup>

建立方程

• 
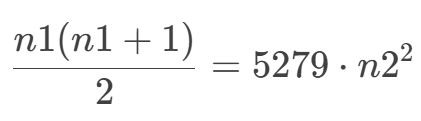
• 两边同时乘以2消去分母

配方转化为平方差形式

映射为佩尔方程x^2−Dy^2=1就是

• x=2n1+1
• D=42232
• y=n2

解题代码构造

• 佩尔方程的解具有递归性,若已知基本解(x1,y1),则所有解可通过以下递推生成

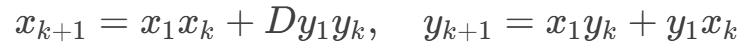
• 通过递归生成解后,需满足n1,n2>2^5279,即:

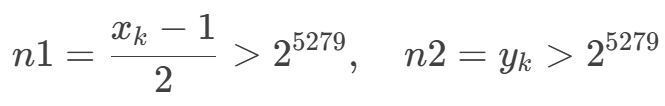
解答:

def solve_pell(D):
    """通过连分数展开法求解佩尔方程的基本解 (x, y)"""
    sqrtD = int(D**0.5)
    if sqrtD**2 == D:
        return None  # D 是平方数，无解
    m, d, a = 0, 1, sqrtD
    h1, h0 = 1, a
    k1, k0 = 0, 1
    while True:
        m = d * a - m
        d = (D - m**2) // d
        a = (sqrtD + m) // d
        h = a * h0 + h1
        k = a * k0 + k1
        if h**2 - D * k**2 == 1:
            return (h, k)
        h1, h0 = h0, h
        k1, k0 = k0, k

def generate_large_solution(D, min_exp):
    """生成满足条件的解 (n1, n2)"""
    min_val = 2**min_exp
    # 基本解
    x1, y1 = solve_pell(D)
    print(f"基本解: x1={x1}, y1={y1}")
    # 生成更大的解直到满足条件
    xk, yk = x1, y1
    while True:
        n1 = (xk - 1) // 2
        n2 = yk
        if n1 > min_val and n2 > min_val:
            return (n1, n2)
        # 通过递归生成下一个解: x_{k+1} = x1*xk + D*y1*yk, y_{k+1} = x1*yk + y1*xk
        x_next = x1 * xk + D * y1 * yk
        y_next = x1 * yk + y1 * xk
        xk, yk = x_next, y_next

D = 42232  # 转换后的佩尔方程系数
min_exp = 0x149f  # 5279 的十六进制，对应 2^5279

try:
    n1, n2 = generate_large_solution(D, min_exp)
    print(f"n1 = {n1}\nn2 = {n2}")
except KeyboardInterrupt:
    print("计算中断，解可能过大或需要优化算法。")

'''
基本解: x1=10863430363390445672094671043496198963286006933268455141841942775234559999, y1=52862312812076818203801374519259164308207980652808243827880652144787200
n1 = 64844564643854949589851602335778398417357958046473541907965865471825503785272678822237542386514416517255501026894654737183875582496807783872409495107534341842017866051238478938990934065677173894545386342407659205001068135302729237100620243248709910469788678708717889604288162784417431423112537621495419154772986757675855167129919386700726005394167383331284254279498630255373138495682828010693186447810574792874994218289604499886574924855123770269452313096224431838804721642376354130042033741778222063044408922159644752291089361532487709307757583423463220655884510805941446159385501144869234562866066430683959981553165969134977445797440777424234638814716724587813493753683564137657751284194240030996768337897606497230343157092891975885036330981018529535961357191249517789661668822447175593069461889888769130598854771926155737315230514752046521202893304056240286346925487675988559705443898301236706180919342302429465894637859344643029018424523547396779994375190095466431959714922380071905524429743822991653088948274069335885888694577809107547976704340333831507724581758450120483610104589803338257974170815964222143136409208762793223834034506152030379364807697319399089566253484223911381851625271939650371513831661159295598370595261204299608982637315116533642003066692618743189177977975115990107686657670079356738239356620676543732171325509902247145583260228629102545738653747438528455898001193543993258829558589125426525550586695373047067726351358183887658916360966276066716968285230497455072503555764167568060675739545960438904928347842532194851125250305537530924233133264250758350828806805623873239302114836480000
n2 = 631077577837315807212150605001212011073700092115983086048740595191397762984508443612849134473582040026490305611506672815790733279455324389749038244192826523764101532018565743490392509759876096077887883254442318175689932630406378290843956256970846767354927615869369288800192989189174422345466133799853927778347597501992783349577759948389598413174615232673353340208973245358433732035960788360390003750780198394158840133454980434734440578601714456186288858206698999555657864335810426614970929557078975227401182253826825384609346528962344036388832502259046741321911200171426780637962405234474461120880834809003855463232063187607331663553796062046207210640552948434337370007381441733734803953072245096582393802864729330924382527356098137452931852934251401785618978991521206247075519888904264778862933717556843876611759454744828205597534256578148852799693013920359743897278354653848976322146722301616470055723006827166136303455670710003638464315811357227470395415655224937948450914818485837106928933473384856351356250618250282625719817648523075398057308035679181355320171871349626866791602751075678767523089354131906867914634157335225214304935483754244074330567251227993002161883809355444153164204811698090714762642324815609182517988506268150630360407065284699130560128074008357903247903494721281244031724949839433411188350035997807588936279816925317066899121998083847631776144099773876703164982929799928344353549122389259490732638723303504957174689978086401613054702247774451584115199235037185582727394255585715896600435834403902988987940547963269504370891849450258752419616559584122132413440460209140828641358681600
'''

提交给靶机后得到账号ADMIN-JM 密码JM001x!

要求以md5[username+password]形式提交flag

import hashlib

def md5_encrypt(input_string):
    md5_obj = hashlib.md5()
    md5_obj.update(input_string.encode('utf-8'))
    return md5_obj.hexdigest()

input_str = "ADMIN-JM+JM001x!"
md5_result = md5_encrypt(input_str)
print(f"MD5加密结果: {md5_result}")
#MD5加密结果: b7133d84297c307a92e70d7727f55cbc