Binary Edwards曲线

题目:

from Crypto.Util.number import bytes_to_long
from flag import flag
assert flag[:5]=='*CTF{' and flag[-1]=='}'
flag=flag[5:-1]
def add(P,Q):
    if Q==0:
        return P
    x1,y1=P
    x2,y2=Q
    return (d1*(x1+x2)+d2*(x1+y1)*(x2+y2)+(x1+x1^2)*(x2*(y1+y2+1)+y1*y2))/(d1+(x1+x1^2)*(x2+y2)),(d1*(y1+y2)+d2*(x1+y1)*(x2+y2)+(y1+y1^2)*(y2*(x1+x2+1)+x1*x2))/(d1+(y1+y1^2)*(x2+y2))

def mul(k,P):
    Q=(0,0)
    while k>0:
        if is_even(k):
            k/=2
            P=add(P,P)
        else:
            k-=1
            Q=add(P,Q)
    return Q

F=GF(2**100)
R.<x,y>=F[]
d1=F.fetch_int(1)
d2=F.fetch_int(1)
x,y=(698546134536218110797266045394L, 1234575357354908313123830206394L)
G=(F.fetch_int(x),F.fetch_int(y))
P=mul(bytes_to_long(flag),G)
print (G[0].integer_representation(),G[1].integer_representation())
print (P[0].integer_representation(),P[1].integer_representation())
#(698546134536218110797266045394L, 1234575357354908313123830206394L)
#(403494114976379491717836688842L, 915160228101530700618267188624L)

解题思路:

分析曲线

我们首先分析一下这是个什么曲线,根据其形式判断其为二元域上的爱德华曲线(Binary Edwards)

其一般形式为

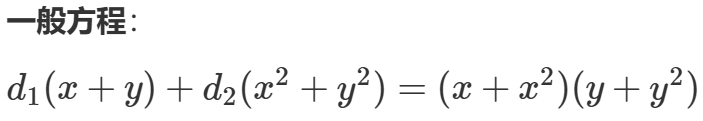![](https://cdn.nlark.com/yuque/0/2025/png/49294098/1742744710677-768c17ef-cd43-4b2d-8f6f-fb3a5ceb4023.png)

分析曲线结构

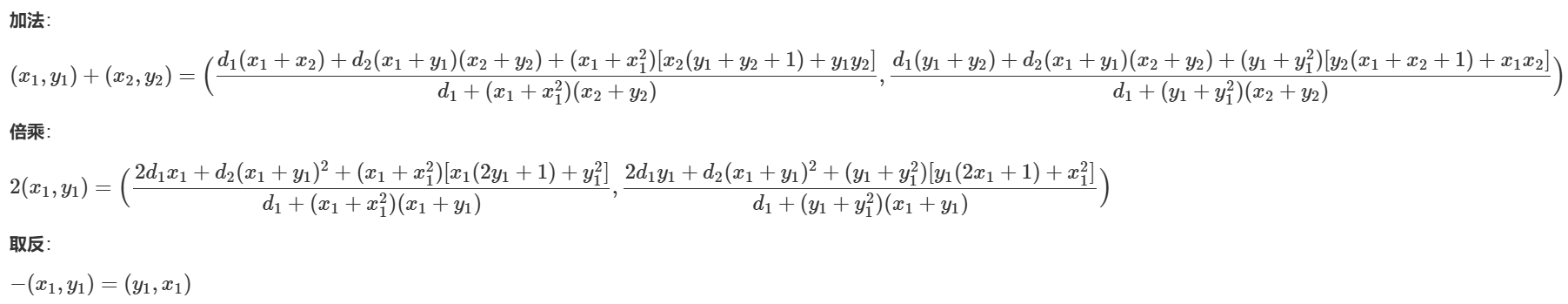
分析代码

**d1**和**d2**:这两个参数在椭圆曲线的加法和乘法操作中被使用,在代码中,d1和d2都被初始化为F.fetch_int(1),即在有限域GF(2100)中的值为1;它们在加法公式中作为系数,影响点的加法运算
**F**:是一个有限域GF(2100),表示一个大小为2100的有限域,在这个域中,所有的运算都是模2100的运算
**x**和**y**:这是椭圆曲线上一个已知点G的坐标,分别表示为长整数,程序通过F.fetch_int将它们转换为有限域GF(2100)中的元素
**G**:这是椭圆曲线上的一个基点,其坐标由x和y给出,程序通过mul函数将flag转换后的整数与基点G相乘,得到加密后的点P
**P**:这是加密后的点,是通过将flag转换为整数后与基点G相乘得到的结果,程序最后输出了P的坐标

add(P,Q)

功能:实现椭圆曲线上两个点P和Q的加法操作
参数:
- P和Q是椭圆曲线上的两个点,每个点是一个二元组(x,y)
逻辑:
- 如果Q=0,返回P,这里的0表示椭圆曲线上的无穷远点
- 否则,计算P和Q的坐标(x1,y1)和(x2,y2)
- 根据椭圆曲线的加法规则,计算新的点R的坐标(x3,y3),这里的加法规则与常见的椭圆曲线加法有所不同,公式中包含了d1和d2作为系数,以及一些特殊的运算(如x1 + x1^2)
输出:返回新的点R的坐标(x3,y3)

mul(k,P)

功能:实现椭圆曲线上点P的标量乘法操作,即计算k×P
参数:
- k是一个整数,表示标量
- P是椭圆曲线上的一个点
逻辑:
- 使用双倍加法算法来实现标量乘法
- 初始化Q=(0,0),表示无穷远点
- 当k>0时:
  - 如果k是偶数,将P加到自身(即P=P+P),并将k除以2
  - 如果k是奇数,将P加到Q上(即Q=Q+P),并将k减1
输出:返回最终的结果Q

解密思路

换元映射

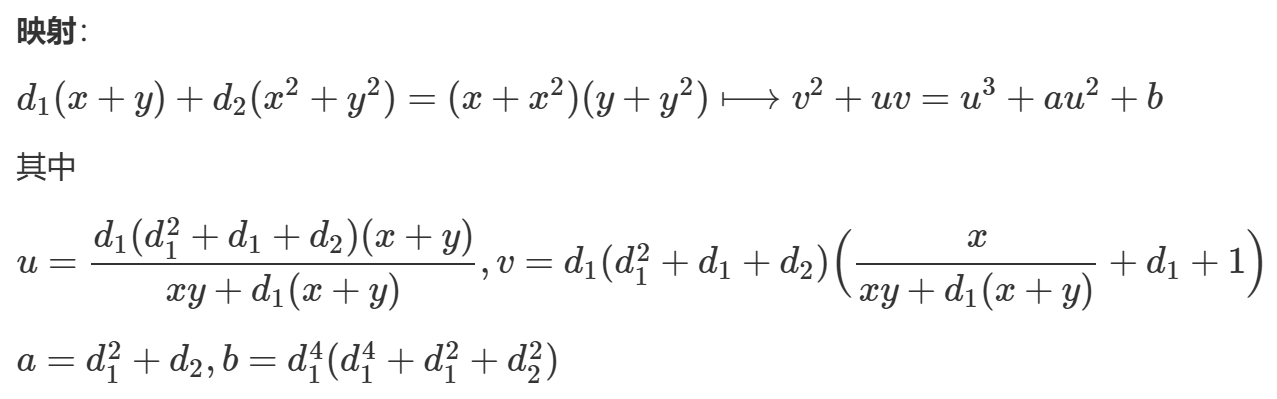
def f(P):
    x,y = P
    u = d1*(d1*d1 + d1 + d2)*(x + y) / (x*y + d1*(x+y))
    v = d1*(d1*d1 + d1 + d2)*(x / (x*y + d1*(x+y)) + d1 + 1)
    return EC(u, v)

然后利用椭圆曲线的离散对数算法求解标量k,使得P=k×G

解答:

F=GF(2**100)
d1=F.fetch_int(1)
d2=F.fetch_int(1)
x,y=(698546134536218110797266045394L, 1234575357354908313123830206394L)
G=(F.fetch_int(x),F.fetch_int(y))

#(698546134536218110797266045394L, 1234575357354908313123830206394L)
x,y = (403494114976379491717836688842L, 915160228101530700618267188624L)
P=(F.fetch_int(x),F.fetch_int(y))


a1 = F.fetch_int(1)
a3 = a4 = F.fetch_int(0)
a2 = d1**2 + d2
a6 = (d1**4)*(d1**4 + d1**2 + d2**2)

EC = EllipticCurve(F, [a1,a2,a3,a4,a6])
def f(P):
    x,y = P
    u = d1*(d1*d1 + d1 + d2)*(x + y) / (x*y + d1*(x+y))
    v = d1*(d1*d1 + d1 + d2)*(x / (x*y + d1*(x+y)) + d1 + 1)
    return EC(u, v)

order = EC.order()

P_ = f(P)
G_ = f(G)

x = discrete_log(P_, G_, operation="+")
print(bytes.fromhex(hex(x)[2:]))
#b'p01Y_Edw@rds'
#*CTF{p01Y_Edw@rds}

posted @ 2025-03-26 23:16 sevensnight 阅读(28) 评论(0) 收藏举报

刷新页面返回顶部

SevensNight

Binary Edwards曲线

题目:

解题思路:

分析曲线

分析代码

解密思路

解答:

公告